Question
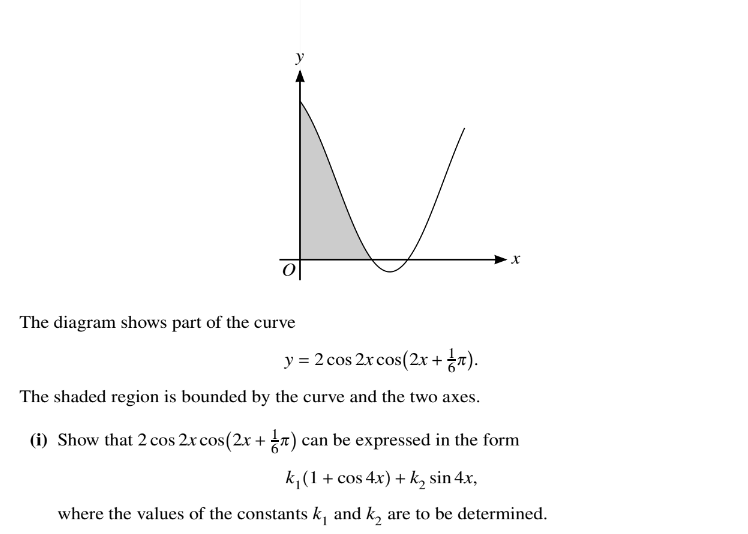
(ii) Find the exact area of the shaded region.
Answer/Explanation
Question
Question
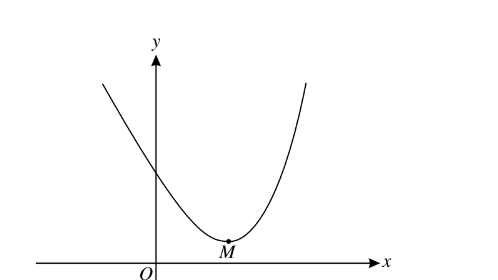
The diagram shows the curve\(y=4e^{\frac{1}{2}x}-6x+3\) and its minimum point M.
(i) Show that the x-coordinate of M can be written in the form ln a, where the value of a is to be stated.
(ii) Find the exact value of the area of the region enclosed by the curve and the lines x = 0, x = 2 and y = 0.
Answer/Explanation
(i) Differentiate to obtain expression of form \(ke^{\frac{1}{2}x}+m\)
Obtain correct \(2e^{\frac{1}{2}x}-6\)
Equate attempt at first derivative to zero and attempt solution
Obtain \( \frac{1}{2}x=\ln 3\) or equivalent
Conclude \(x=\ln 9\) or a=9
(ii) Integrate to obtain expression of form \(ae^{\frac{1}{2}x}+bx^{2}+cx\)
Obtain correct \(8e^{\frac{1}{2}x}-3x^{2}+3x\)
Substitute correct limits and attempt simplification
Obtain 8e – 14
Question
Question
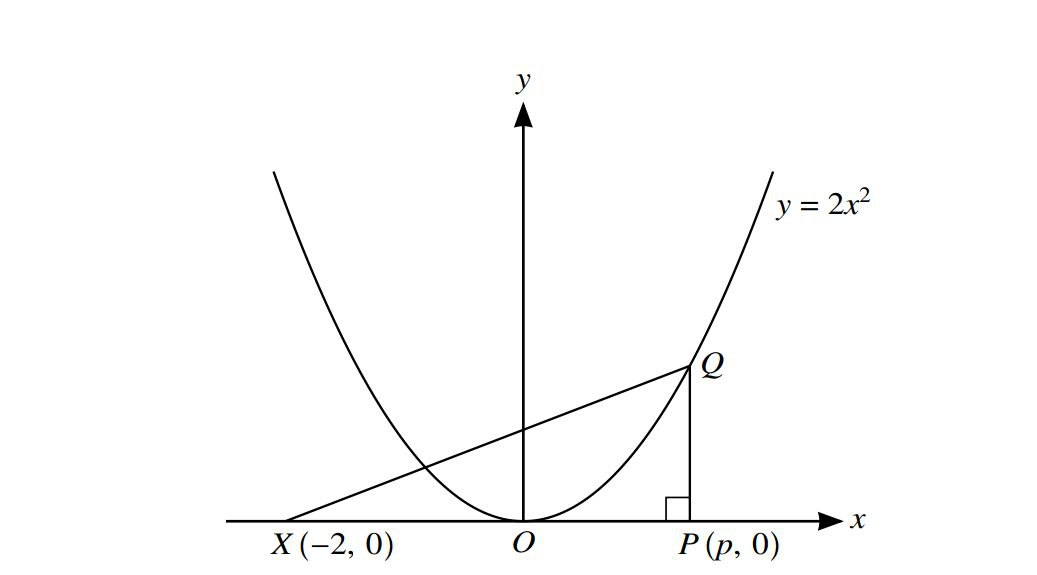
The diagram shows the curve \(y=2x^{2}\) and the points X(-2,0) and P(p,0).The point Q lies on the curve and PQ is parallel to the y-axis.
(i)_Express the area,A,of trioangle XPQ in terms of p.
The point P moves along the x-axis at a constant rate of 0.02 units per second and Q moves along the curve so that PQ remains to the y-axis.
(ii)Find the rate at which A is increasing when p=2.
Answer/Explanation
(i)\(A=\frac{1}{2}\times \left ( 2+p \right )\times 2p^{2}=2p^{2}+p^{3}\)
(ii)\(\frac{\mathrm{d} A}{\mathrm{d} p}=4p+3p^{2}\)
\(\frac{\mathrm{d} A}{\mathrm{d} t}=\frac{\mathrm{d} A}{\mathrm{d} p}\times \frac{\mathrm{d} p}{\mathrm{d} t}=0.02\times 20=0.4\)
or\( \frac{\mathrm{d} A}{\mathrm{d} t}=4p\frac{\mathrm{d} p}{\mathrm{d} t}+3p^{2}\frac{\mathrm{d} p}{\mathrm{d} t}\)
Question
Question
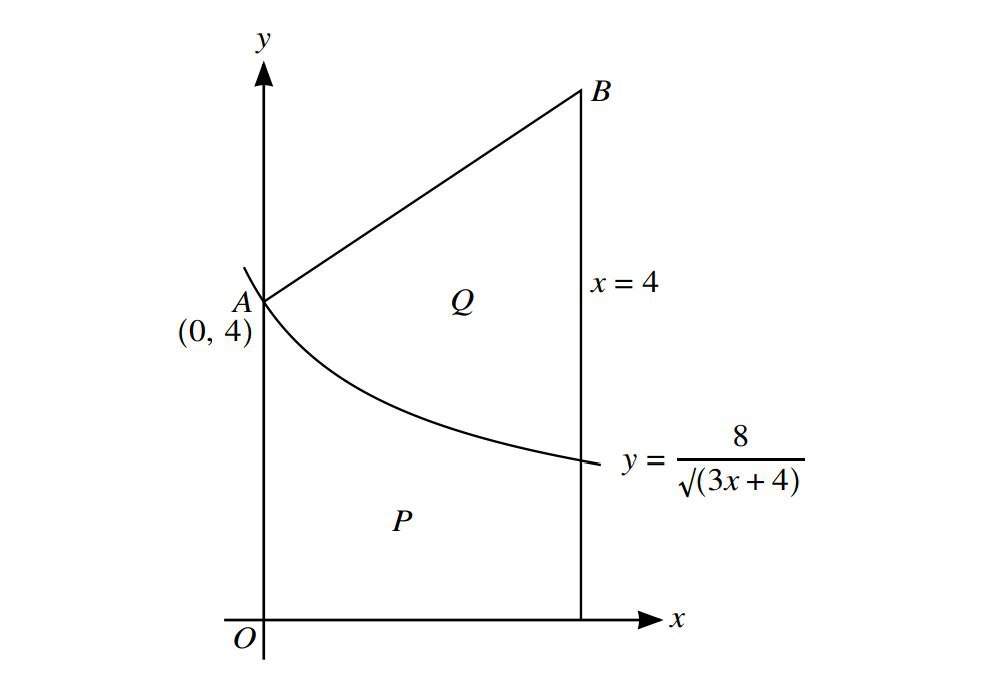
The diagram shows part of the curve \(*y=\frac{8}{\sqrt{3x+4}}\) .The curve intersects the y-axis at A(0,4).The normal to the curve at A intersects the line x=4 at the pointB.
(i)Find the coordinates of B.
(ii)Show with all necessary working, that the areas of the regions marked P and Q are equal.
Answer/Explanation
(i)\( \frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{4}{\left ( 3x+4 \right )^{\frac{3}{2}}}\times 3\)
\(\rightarrow m_{(x=0)}=-\frac{3}{2}\) Perpendicular\( \rightarrow m_{(x=0)}=\frac{2}{3}\)
Equation \(y-4=\frac{2}{3}(x-0)\)
Meets x=4 at \(B\left ( 4,\frac{20}{3} \right )\)
(ii)\(\int \frac{8}{\sqrt{\left ( 3x+4 \right )}}dx=\frac{8\sqrt{(3x+4)}}{\frac{1}{2}}\div 3\)
Limits from 0 to 4\(\rightarrow Area P=\frac{32}{3}\)
Area Q=Trapezium-P
Area of Trapezium=\(\frac{1}{2}\left ( 4+\frac{20}{3} \right )\times 4=\frac{64}{3}\)
Area of P and Q are both \(\frac{32}{3}\)
Question
Question
A line has equation y=2x+c and a curve has equation \(y=8-2x-x^{2}\).
(i)For the case where the line is a tangent to the curve ,find the value of the constant c.
(ii)For the case wjhere c=11,find the x-coordinates of the points of intersection of the line and the curve.Find also, by integration, the area of the region between the line and the curve.
Answer/Explanation
(i)\(x^{2}+4x+c-8=0\)
\(16-4(c-8)=0\)
c=12
OR
\(-2-2x=2\rightarrow x=-2\)
-4+c=8+4-4
c=12
(ii)\(x^{2}+4x+3\rightarrow \left ( x+1 \right )\left ( x+3 \right )=0\)
x=-1 or -3
\(\int \left ( 8-2x-x^{2} \right )-\left [ \int \left ( 2x+11 \right ) \right ]\) or area of trapezium
\(\left [ 8x-x^{2}-\frac{x^{3}}{3} \right ]-\left [ x^{2}+11x \right ]\) or \(\left [ 8x-x^{2}-\frac{x^{3}}{3} \right ]-\frac{1}{2}\left ( 5+9 \right )\times 2\)
Apply their limits to at least integral for curve \(1\tfrac{1}{3}\)
Question
Question
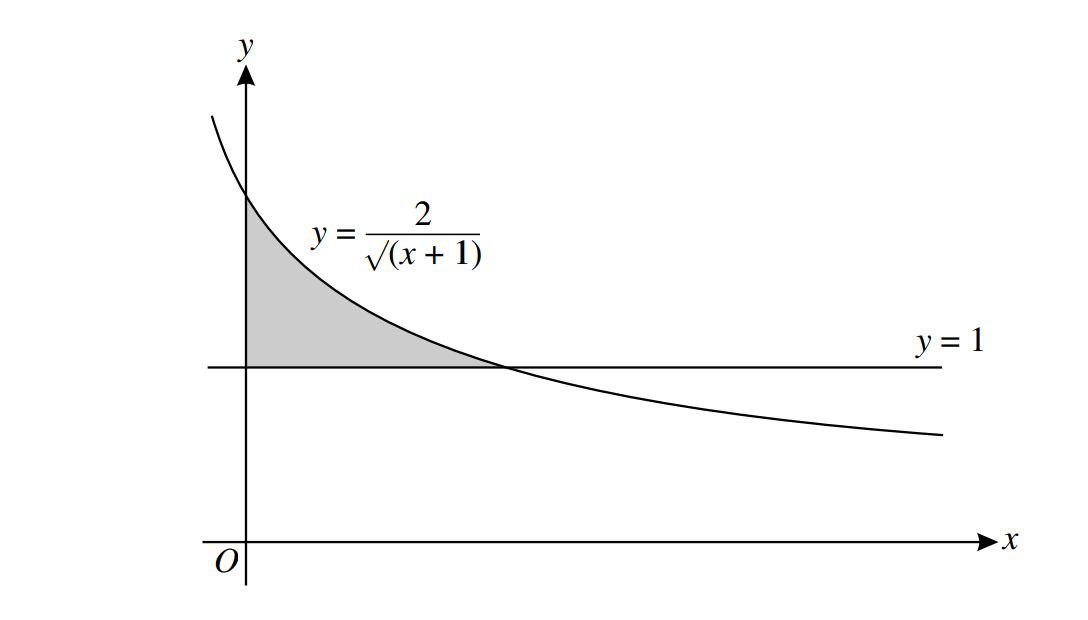
The diagram shows the line y=1 and the part of the curve \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\).
(i)Show that the equation \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\) can be written in the form \(x=\frac{4}{y^{2}}-1\)
(ii)Find \(\int \left ( \frac{4}{y^{2}}-1 \right )dy\).Hence find the area of the shaded region.
(ii)The shaded region is rotated through about the y-axis.Find the exact value of the volume of revolution obtained.
Answer/Explanation
(i) \(x=\frac{4}{y^{2}}-1\)
(ii)\(\int \left ( \frac{4}{y^{2}}-1 \right )dy=\left [- \frac{4}{y} -y\right ]\)
\(^{2}_{1}\left [ -\frac{4}{2}-2-\left ( -4-1 \right ) \right ]\)
(iii)\(\pi \int x^{2}dy=\left ( \pi \right )\int \left ( \frac{16}{y^{4}}-\frac{8}{y^{2}} +y\right )\)
\(\left ( \pi \right )\left [ -\frac{16}{3y^{3}}+\frac{8}{y} +y\right ]\)
\(\left ( \pi \right )\left [\left ( -\frac{16}{24}+4+2 \right )-\left ( -\frac{-16}{3}+8+1\right )\right ]\)
\(\frac{5\pi }{3}\)
Question
Question
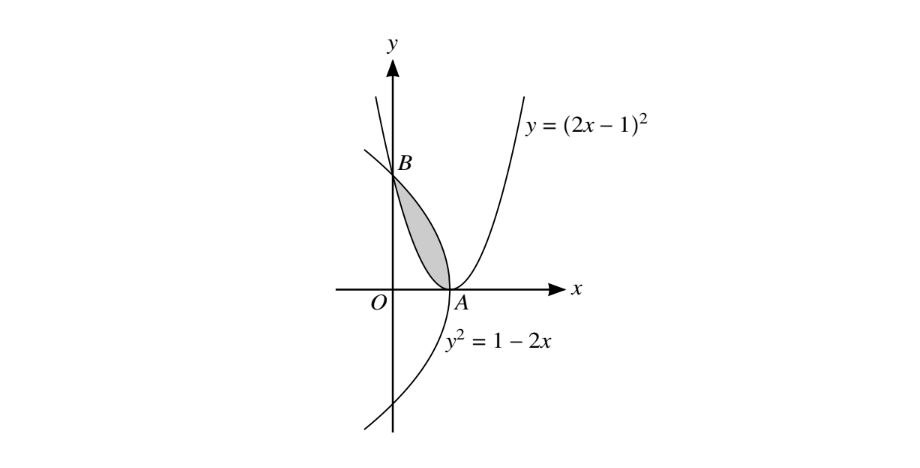
The diagram shows parts of the curves \(y=\left ( 2x-1 \right )^{2}\) and \(y^{2}=1-2x\), intersecting at points A AND b.
(i) State the coordinates of A
(ii)Find,showing all necessary working, the area of the shaded region.
Answer/Explanation
(i)\(A=\left ( \frac{1}{2},0 \right )\)
(ii)\( \int \left ( 1-2x \right )^{\frac{1}{2}}dx=\left [ \frac{\left ( 1-2x \right )^{\frac{3}{2}}}{\frac{3}{2}} \right ]\left [ \div \left ( -2 \right )\right ]\)
\(\int \left ( 2x-1 \right ) ^{2}dx=\left [ \frac{\left ( 2x-1 \right )^{3}}{3} \right ]\left [ \div 2 \right ]\)
\(\left [ 0-\left ( -\frac{1}{3} \right ) \right ]-\left [ 0-\left (- \frac{1}{6} \right ) \right ]\)
\(\frac{1}{6}\)
Question
Question
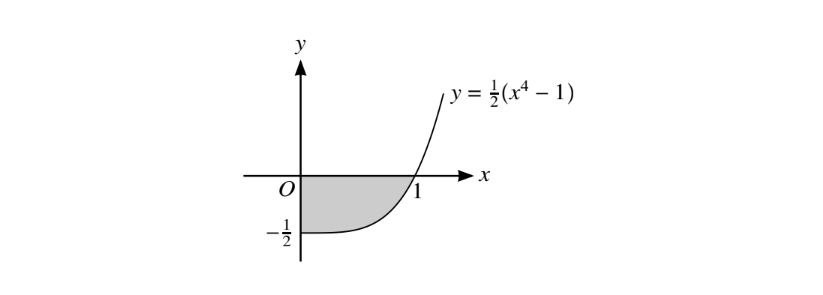
The diagram shows part of the curve \(y=\frac{1}{2}\left ( x^{4}-1 \right )\),defined for\( x\geq 0\)
(i)Find, showing all necessary working ,the area of shaded region.
(ii)Find, showing all necessary working, the volume obtained when the shaded region is rotated through \(360^{\circ}\) about the axis.
(iii)Find, showing all necessary working, the volume obtained when the shaded region is rotated through \(360^{\circ}\) about the y-axis.
Answer/Explanation
(i)Area=\(\int \frac{1}{2}\left ( x^{4} -1\right )dx=\frac{1}{2}\left [ \frac{x^{5}}{5} -x\right ]\)
\(\frac{1}{2}\left [ \frac{1}{5}-1 \right ]-0=-\left (\frac{2}{5} \right )\)
(ii)\(Vol=\pi \int y^{2}dx=\frac{1}{4}\int \left ( x^{8}-2x^{4}+1 \right )dx\)
\(\frac{1}{4}\left ( \pi \right )\left [ \frac{x^{9}}{9}-\frac{2x^{5}}{5}+x \right ]\)
\(\frac{1}{4}\left ( \pi \right )\left [ \frac{1}{9}-\frac{2}{5}+1 \right ]-0\)
\(\frac{8\pi }{45}\) or 0.559
(iii)\(Vol=\pi \int x^{2}dy=\left ( \pi \right )\int \left ( 2y+1` \right )^{\frac{1}{2}}dy\)
\(\pi \left [ \frac{\left ( 2y+1 \right )^{\frac{3}{2}}}{\frac{3}{2}} \right ]\left [ \div 2 \right ]\)
\(\left ( \pi \right )\left [ \frac{1}{3} -0\right ]\)
\(\frac{\pi }{3}\) or 1.05
Question
Question
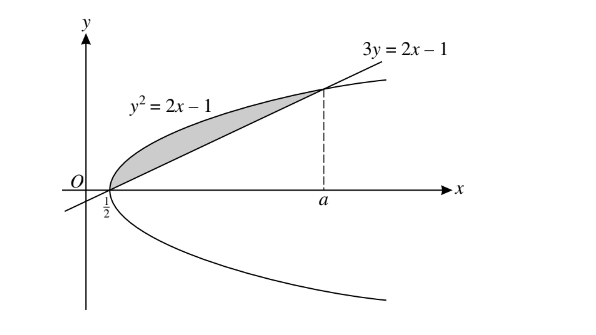
The diagram show the curve \(y^{2}=2x-1\) and the straight line 3y=2x-1.The curve and thew straight line intersect at \(x=\frac{1}{2}\) and x=a and ,where a is a constant.
(i)Show that a=5.
(ii)Find,showing all necessary working ,the area of the shaded region.
Answer/Explanation
(i)\(y^{2}=3y\Rightarrow y(y-3)=0\Rightarrow y=3\) or 0
\(x=\frac{1}{2}\) or 5 \(\Rightarrow a=5\)
(ii)\(\left [ \frac{\left ( 2x-1 \right )^{\frac{3}{2}}}{\frac{3}{2}} \right ]\div 2\)
\(\left [ \frac{2}{3}\times \frac{x^{2}}{2}-\frac{x}{3} \right ]\)
\(\left [ \frac{27}{9}-0 \right ]\) \( \left [ \frac{25}{3}-\frac{5}{3}-\left ( \frac{1}{12}-\frac{1}{6} \right ) \right ]\)
\(\frac{9}{4}\)
Question
Question
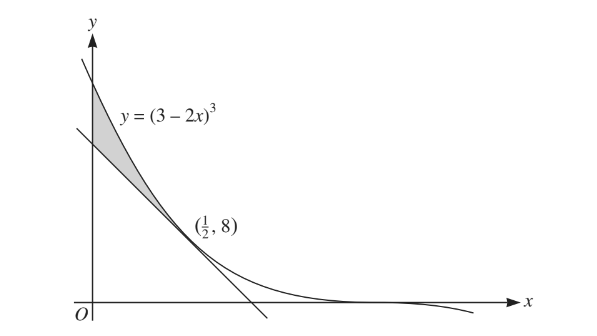
The diagram shows the curve \(y=\left ( 2-3x \right )^{3}\) and the tangent to the curve at the point \(\left ( \frac{1}{2},8 \right )\)
(i) Find the equation of this tangent, giving your answer in the form y = mx + c.
(ii) Find the area of the shaded region.
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ 3(3-2x)^{2} \right ]\times \left [ -2 \right ]\)
At \(x=\frac{1}{2}\) ,\(\frac{\mathrm{d} y}{\mathrm{d} x}=-24\)
\(y-8=-24(x-\frac{1}{2})\)
y=-24x+20
(ii)Area under curve=\(\left [ \frac{(3-2x)^{4}}{4} \right ]\times \left [ -\frac{1}{2} \right ]\)
\(-2-(-\frac{81}{8})\)
Area under tangent=\(\int \left ( -24x+20 \right )\)
\(=\left | -12x^{2}+20x \right |\) or 7
\(\frac{9}{8}\) or 1.125
Question
(a) In an arithmetic progression the sum of the first ten terms is 400 and the sum of the next ten terms is 1000. Find the common difference and the first term.
(b) A geometric progression has first term a, common ratio r and sum to infinity 6. A second geometric progression has first term 2a, common ratio \(r^{2}\) and sum to infinity 7. Find the values of a and r.
Answer/Explanation
(a)\(\frac{10}{2}(2a+9d)=400\)
\(\frac{20}{2}(2a+19d)=1400\)
\(\frac{10}{2}\left [ 2(a+10d)+9d \right ]=1000\)
d=6 a=13
(b)\(\frac{a}{1-r}=6 \) \(\frac{2a}{1-r^{2}}=7\)
\(\frac{12(1-r)}{1-r^{2}}=7\) or \(\frac{1-r^{2}}{1-r}=\frac{12}{7}\)
\(r=\frac{5}{7}\) or 0.714
\(a=\frac{12}{7}\) or 1.714
Question
Question
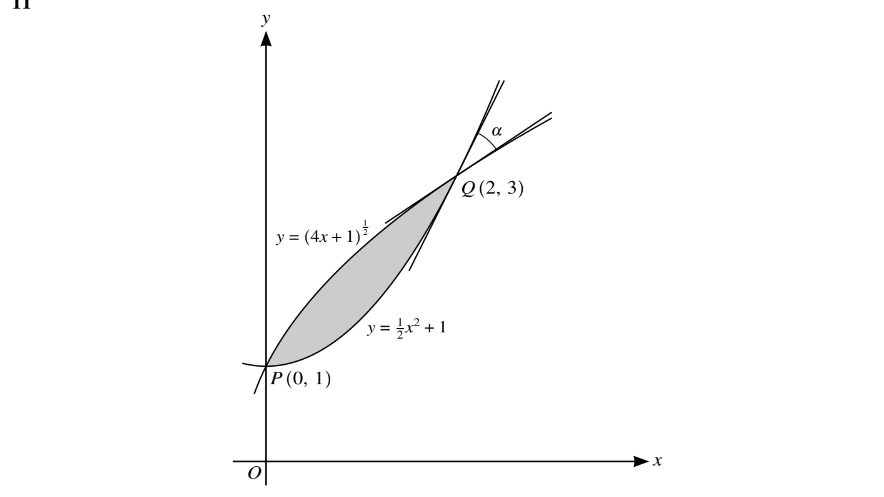
The diagram shows parts of the curves \(y=(4x+1)^{\frac{1}{2}}\) and \(y=\frac{1}{2}x^{2}+1\) intersecting at points P (0, 1) and Q( 2, 3). The angle between the tangents to the two curves at Q is \(\alpha \).
(i) Find \(\alpha \), giving your answer in degrees correct to 3 significant figures.
(ii) Find by integration the area of the shaded region.
Answer/Explanation
(i)For \(y=\left ( 4x+1 \right )^{\frac{1}{2}}\) ,
\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ \frac{1}{2}\left ( 4x+1 \right ) ^{-\frac{1}{2}}\right ]\times 4\)
When x=2,gradient \(m_{1}=\frac{2}{3}\)
For \(y=\frac{1}{2}x^{2}+1\),\(\frac{\mathrm{d} y}{\mathrm{d} x}=x\) → gradient \( m_{2}=2\)
\(\alpha =\tan ^{-1}m_{2}-\tan ^{-1}m_{1}\)
\(\alpha =63.43-33.69=29.7\)
Question
Question.
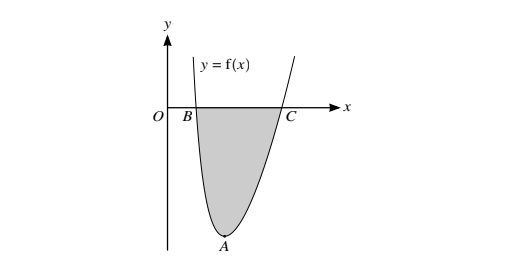
The diagram shows the curve \(y = f(x).\) defined for x > 0. The curve has a minimum point at A and
crosses the x-axis at B and C. It is given that \(\frac{\partial y}{\partial x}=2x-\frac{2}{x^3}\) and that the curve passes through the point \((4,\frac{189}{6})\)
(i) Find the x-coordinate of A
(ii) Find f(x).
(iii) Find the x-coordinates of B and C.
(iv) Find, showing all necessary working, the area of the shaded region.
Answer/Explanation
(i) \(\frac{2x-2}{x^{3}}=0\)
\(x^{4}=1\Rightarrow x=1\) at A cao
(ii)\(f\left ( x \right )=\frac{x^{2}+1}{x^{2}}\left ( +c \right )\) cao
\(\frac{189}{16}=\frac{16+1}{16+c}\)
\(c=-\frac{17}{4}\)
(iii) \(\frac{x^{2}+1}{x^{2}-\frac{17}{4}}=0\Rightarrow 4x^{4}-17x^{2}+4\left ( =0 \right )\)
\(\left ( 4x^{2} -1\right )\left ( x^{2}-4 \right )\left ( =0 \right )\)
\(x=\frac{1}{2},2\)
(iv)\( \int \left (\frac{ x^{2}+x^{-2}-17 }{4}\right )dx=\frac{x^{3}}{3}-\frac{1}{x}-\frac{17x}{4}\)
\(\left ( \frac{8}{3}-\frac{1}{2}-\frac{17}{2} \right )-\left ( \frac{1}{24}-2-\frac{17}{8} \right )\)
\(Area=\frac{9}{4}\)
Question
Question.
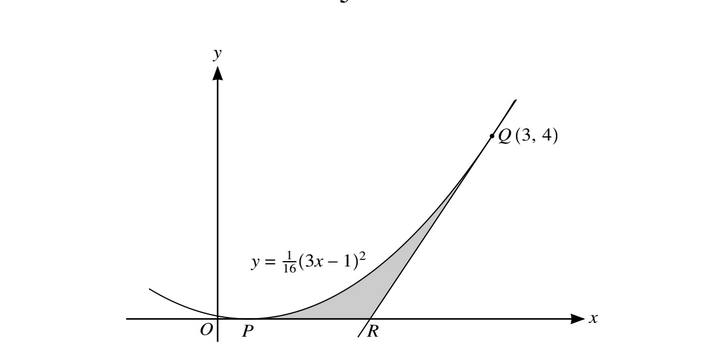
The diagram shows part of the curve \(y =\frac{1}{16}(3x – 1)^2\) which touches the x-axis at the point P. The point Q (3, 4) lies on the curve and the tangent to the curve at Q crosses the x-axis at R.
Showing all necessary working, find by calculation
(i) State the x-coordinate of P.
(ii) the x-coordinate of R,
(iii) the area of the shaded region PQR.
Answer/Explanation
Ans:(i) \(x=\frac{1}{3}\)
(ii) \(\frac{\partial y}{\partial x}=\left [ \frac{2}{16} (3x-1)\right ]\left [ 3\right ]\)
\(when x=3 n \to \frac{\partial y}{\partial x}=3\)
\(Equation or QR is y-4=3(x-3)\)
\(when y=0 \rightarrow x=\frac{5}{3}\)
(iii)Area under curve \(=\left [ \frac{1}{16\times 3}(3x-1)^3 \right ]\times \left [ \frac{1}{3} \right ]\)
\(\left [ \frac{1}{16\times 9}(8^3 -0)\right ]=\frac{32}{9}\)
Area of \(\Delta =\frac{8}{3}\)
Shaded area\( = \frac{32}{9}-\frac{8}{3}=\frac{8}{9}\)
Question
Question
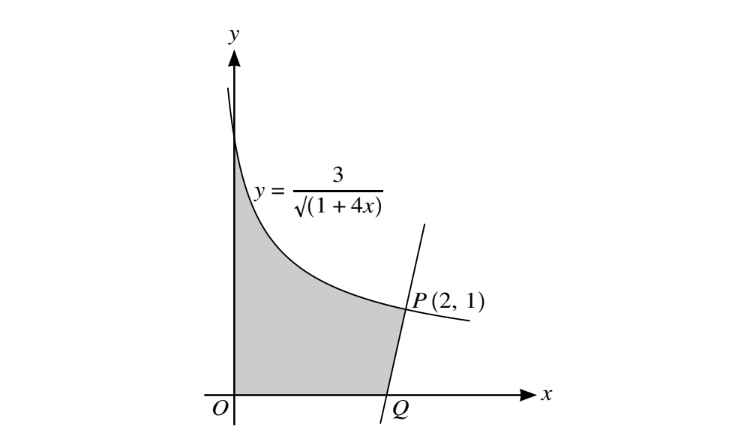
The diagram shows part of the curve\( y = \frac{3}{\sqrt({1+4x})} \) and a point P (2, 1) lying on the curve. The normal to the curve at P intersects the x-axis at Q.
(i) Show that the x-coordinate of Q is \(\frac{16}{9}\)
(ii) Find, showing all necessary working, the area of the shaded region.
Answer/Explanation

Question
Question

The diagram shows part of the curve\( y = \frac{3}{\sqrt({1+4x})} \) and a point P (2, 1) lying on the curve. The normal to the curve at P intersects the x-axis at Q.
(i) Show that the x-coordinate of Q is \(\frac{16}{9}\)
(ii) Find, showing all necessary working, the area of the shaded region.
Answer/Explanation

Question
Question
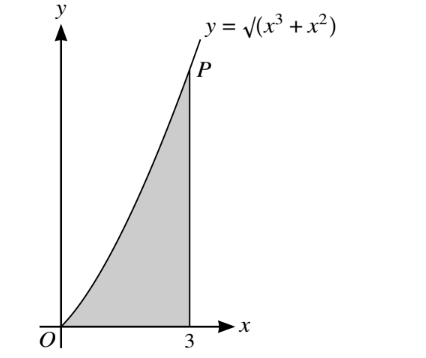
The diagram shows part of the curve with equation \(y=\sqrt{x^{3}+x^{2}}\) The shaded region is bounded by the curve, the x- axis and the line x = 3.
(i) Find, showing all necessary working, the volume obtained when the shaded region is rotated
through 360Å about the x-axis.
(ii) P is the point on the curve with x-coordinate 3. Find the y-coordinate of the point where the
normal to the curve at P crosses the y-axis.
Answer/Explanation
9(i)
\(V=(\Pi)\int (x^{3}+x^{2})(dx)\)
\(=(\Pi )\left [ \frac{x^{4}}{4} +\frac{x^{3}}{3}\right ]_{0}^{3}\)
\(=\Pi \left [ \frac{81}{4}+9 -(0) \right ]\)
\(=\frac{117\Pi }{4}\)
9(ii)
\(\frac{dy}{dx}=\frac{1}{2}(x^{3}+x^{2})\times (3x^{2^{}+}2x)\)
At (x = 3,y = 6)
At \(x=3,m=\frac{1}{2}\times \frac{1}{6}\pm \times 33=\frac{11}{4}\)
Equation of normal is
\(y-6=-\frac{4}{11}(x-3)\)
When
x = 0, y =\(\frac{78}{11}\)
Question
Question
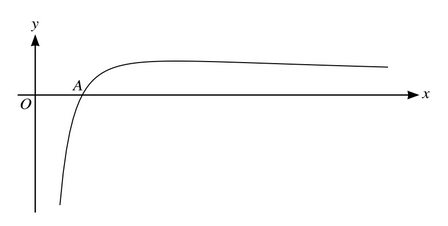
The diagram shows the curve with equation \(y=9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})\). The curve crosses the x-axis at the point A.
(a) Find the x-coordinate of A.
(b) Find the equation of the tangent to the curve at A.
(c) Find the x-coordinate of the maximum point of the curve.
(d) Find the area of the region bounded by the curve, the x-axis and the line x=9.
Answer/Explanation
Ans:
(a) \(9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})=0\) leading to \(9x^{-\frac{3}{2}(x-4)=0\)
x=4 only
(b) \(\frac{dy}{dx}=9(-\frac{1}{2}x^{-\frac{3}{2}}+6x^{-\frac{5}{2}})\)
At x = 4 gradient \(=9(-\frac{1}{16}+\frac{6}{32})=\frac{9}{8}\)
Equation is \(y=\frac{9}{8}(x-4)\)
(c) \(9x^{-\frac{5}{2}}(-\frac{1}{2}x+6)=0\)
x=12
(d) \(\int 9(x^{-\frac{1}{2}}-4x^{-\frac{3}{2}})dx=9(\frac{x^{\frac{1}{2}}}{\frac{1}{2}}-\frac{4x^{-\frac{1}{2}}}{-\frac{1}{2}})\)
\(9[(6+\frac{8}{3})-(4+4)]\)
6
Question
Question
The equation of a curve is \(y=2\sqrt{3x+4}-x\)
(a) Find the equation of the normal to the curve at the point (4, 4), giving your answer in the form
y = mx + c. [5]
(b) Find the coordinates of the stationary point. [3]
(c) Determine the nature of the stationary point. [2]
(d) Find the exact area of the region bounded by the curve, the x-axis and the lines x = 0 and x = 4. [4]
Answer/Explanation
Ans
11 (a) \(\frac{dx}{dy}=3(3x+4)^{-0.5}-1\)
Gradient of tangent \(=-\frac{1}{4}\) and Gradient of normal = 4
Equation of line is (y – 4) = 4(x – 4) or evaluate c
So y = 4x – 12
11 (b) 3(3x+4)-0.5 -1 = 0
Solving as far as x=
\(x=\frac{5}{3}, y=2\left ( 3\times \frac{5}{3}+4 \right )^{0.5}-\frac{5}{3}=\frac{13}{3}\)
At \(x=\frac{5}{3} \frac{d^{2}y}{dx^{2}}\) is negative so the point is a maximum
11 (d) \(Area-[f2(3x+4)^{0.5}-xdx=]\frac{4}{9}(3x+4)^{1.5}-\frac{1}{2}x^{2}\)
\(\left ( \frac{4}{9}(16)^{1.5}-\frac{1}{2}(4)^{2} \right )-\frac{4}{9}(4)^{1.5}=\frac{256}{9}-8-\frac{32}{9}\)
\(16\frac{8}{9}\)
