Question
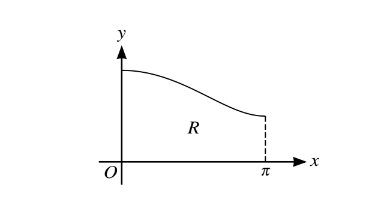
The diagram shows the curve with equation\( y =\sqrt{(1+3cos^{2}(\frac{1}{2}))}\)for 0 ≤ x ≤ 0. The region R is bounded by the curve, the axes and the line x =\( \pi\) .
(i) Use the trapezium rule with two intervals to find an approximation to the area of R, giving your answer correct to 3 significant figures.
(ii) The region R is rotated completely about the x-axis. Without using a calculator, find the exact volume of the solid produced.
▶️Answer/Explanation
(i)Using y-values: \(2\sqrt{2.5}\), \(1\)
The formula for the trapezium rule with n intervals is:
\(A \approx \frac{h}{2}\left[f\left(x_0\right)+2 \sum_{i=1}^{n-1} f\left(x_i\right)+f\left(x_n\right)\right]\)
\(h = \frac{1}{2}\pi\)
\(V = \frac{1}{2} \cdot \frac{1}{2}\pi \left(2 + \sqrt{2.5} + 1\right)\)
\(V = \frac{1}{4}\pi \left(2 + \sqrt{2.5} + 1\right)\)
\(V \approx 4.84\)
(ii) To find the exact volume, we’ll use the integral:
\(V = \int \pi \left(1 + 3\cos^2\left(\frac{1}{2}x\right)\right)dx\)
Now, we’ll use the appropriate identity to express the integrand in the form \(k_1 + k_2\cos(x)\):
\(3\cos^2\left(\frac{1}{2}x\right) = \frac{3}{2} + \frac{3}{2}\cos(x)\)
\(V = \int \pi \left(1 + \frac{3}{2} + \frac{3}{2}\cos(x)\right)dx\)
\(V = \pi \int \left(\frac{5}{2} + \frac{3}{2}\cos(x)\right)dx\)
\(V = \pi \left[\frac{5}{2}x + \frac{3}{2}\sin(x)\right] + C\)
Now, we need to evaluate this expression between the limits \(\pi\) and \(0\):
\(V = \pi \left(\frac{5}{2}\pi + \frac{3}{2}\sin(\pi) – \frac{5}{2}(0) – \frac{3}{2}\sin(0)\right)\)
\(V = \pi \left(\frac{5}{2}\pi + 0 – 0 – 0\right)\)
\(V = \frac{5}{2}\pi^2\)
So, the exact volume of the solid is \(\frac{5}{2}\pi^2\),
Question
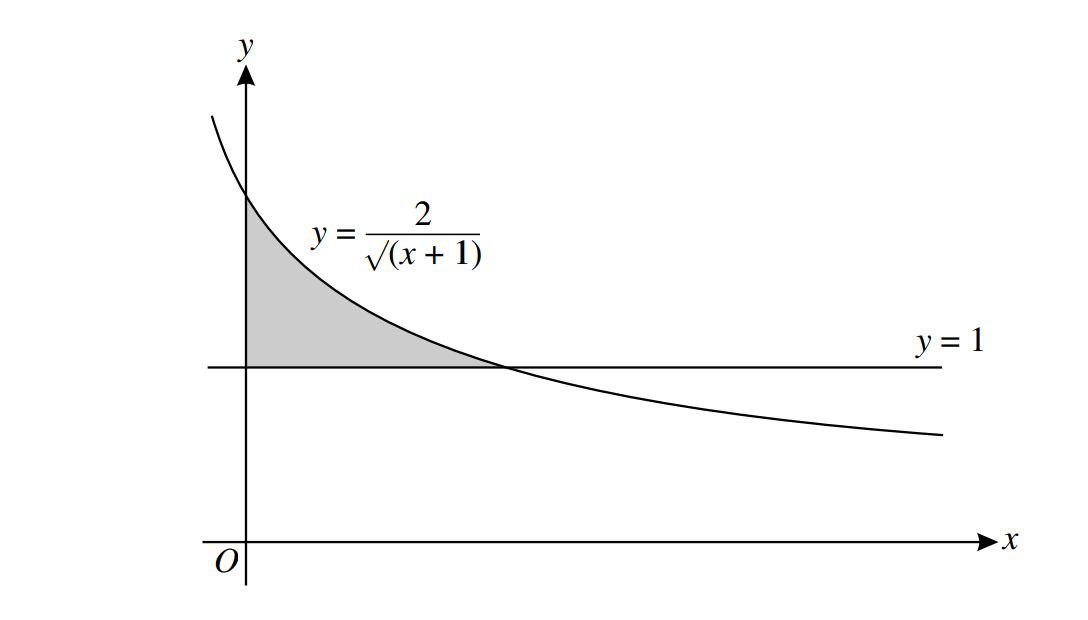
The diagram shows the line y=1 and the part of the curve \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\).
(i)Show that the equation \(y=\frac{2}{\sqrt{\left ( x+1 \right )}}\) can be written in the form \(x=\frac{4}{y^{2}}-1\)
(ii)Find \(\int \left ( \frac{4}{y^{2}}-1 \right )dy\).Hence find the area of the shaded region.
(ii)The shaded region is rotated through about the y-axis.Find the exact value of the volume of revolution obtained.
▶️Answer/Explanation
(i) To show that the equation \(y = \frac{2}{\sqrt{x+1}}\) can be written in the form \(x = \frac{4}{y^2} – 1\), we’ll start by manipulating the given equation:
\(y = \frac{2}{\sqrt{x+1}}\)
\(y\sqrt{x+1} = 2\)
\(y^2(x+1) = 4\)
\(x+1 = \frac{4}{y^2}\)
\(x = \frac{4}{y^2} – 1\)
(ii) \(\int \left(\frac{4}{y^2} – 1\right) dy = \left[-\frac{4}{y} – y\right]_1^2\)
\(\left[-\frac{4}{2} – 2 – \left(-\frac{4}{1} – 1\right)\right]\)
\(-2 – 2 + 4 + 1\)
=\(1\)
So, the area of the shaded region is indeed \(1\) square unit.
(iii) For the volume of revolution,
\(\pi \int x^2 dy = (\pi) \int \left(\frac{16}{y^4} – \frac{8}{y^2} + y\right) dy\)
\((\pi) \left[-\frac{16}{3y^3} + \frac{8}{y} + y\right]\)
\((\pi)\left[\left(-\frac{16}{3(2)^3} + \frac{8}{2} + 2\right) – \left(-\frac{16}{3(1)^3} + \frac{8}{1} + 1\right)\right]\)
\((\pi)\left[-\frac{16}{24} + 4 + 2 – \left(-\frac{16}{3} + 8 + 1\right)\right]\)
\(\frac{5\pi}{3}\)
So, the exact volume of revolution obtained is indeed \(\frac{5\pi}{3}\) cubic units.
Question
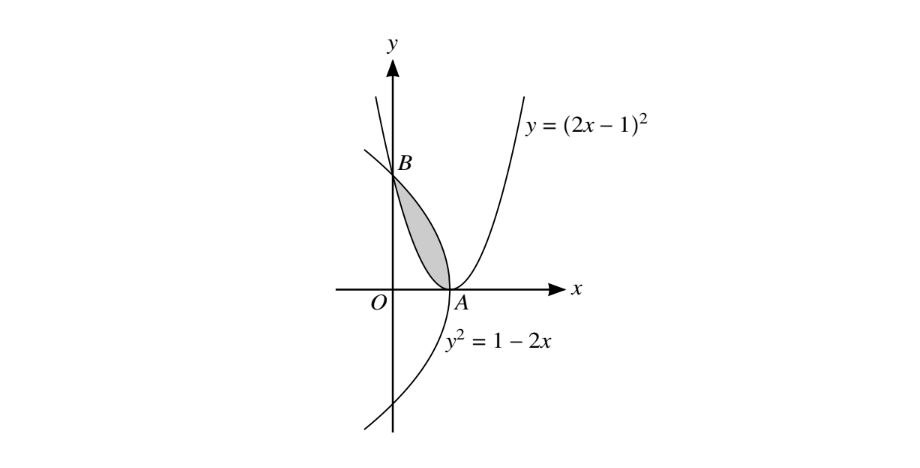
The diagram shows parts of the curves \(y=\left ( 2x-1 \right )^{2}\) and \(y^{2}=1-2x\), intersecting at points A AND b.
(i) State the coordinates of A
(ii)Find,showing all necessary working, the area of the shaded region.
▶️Answer/Explanation
(i) To state the coordinates of point A, we need to find the intersection of the two given curves \( y = (2x – 1)^2 \) and \( y^2 = 1 – 2x \).
Set y^{2}=(1-2x)^{2} to fund the x-coordinates of the intersection points:
\((2x – 1)^2 = 1 – 2x \)
\( 4x^2 – 4x + 1 = 1 – 2x \)
\( 4x^2 – 4x + 2x = 0 \)
\( 4x^2 – 2x = 0 \)
\( x(4x – 2) = 0 \)
\( x = 0 \) or \( x = \frac{1}{2} \)
Now lets find corresponding y-coordinates for each x-value.
For x=0
\(y^{2}=1-2(0)\)
\(y^{2}=1\)
\(y=\pm 1\)
However, by examining the graph, it is clear that the intersection at x = 0 is at the origin where y is also 0, so for point A which is the lower intersection point, A(0,0).
For\( x=\frac{1}{2}\), we find y using the equation \(y=(2x-1)^{2}\)
\(y=(2(\frac{1}{2})-1)^{2}\)
\(y=(1-1)^{2}\)
y=0
So the coordinates of point B, the upper intersection point, are:
\(B\left ( \frac{1}{2},0 \right )\)
(ii) To find the area of the shaded region, we will integrate the difference between the two curves from the left intersection point to the right intersection point.
We already know one of the intersection points is at \( x = 0 \). We need to find the other intersection point, which we can call point B. Since we found that \( x = \frac{A(0)1}{2} \) is also a solution to the equation above, we’ll use that as the \( x \)-coordinate of point B.
Now, let’s find the \( y \)-coordinate for point B using \( x = \frac{1}{2} \) in the equation \( y = (2x – 1)^2 \):
\( y = \left(2\left(\frac{1}{2}\right) – 1\right)^2 = (1 – 1)^2 = 0 \)
So, point B is \( \left(\frac{1}{2}, 0\right) \).
To find the area of the shaded region, we integrate from \( x = 0 \) to \( x = \frac{1}{2} \). The top function is \( y = (2x – 1)^2 \) and the bottom function is the \( x \)-axis, which is \( y = 0 \). Thus, the area \( A \) is given by:
\( A = \int_{0}^{\frac{1}{2}} \left((2x – 1)^2 – 0\right) dx \)
\( A = \int_{0}^{\frac{1}{2}} (4x^2 – 4x + 1) dx \)
\( A = \left[ \frac{4}{3}x^3 – 2x^2 + x \right]_{0}^{\frac{1}{2}} \]\)
Evaluate this at \( x = \frac{1}{2} \) and \( x = 0 \), and subtract the latter from the former:
\( A = \left( \frac{4}{3}\left(\frac{1}{2}\right)^3 – 2\left(\frac{1}{2}\right)^2 + \frac{1}{2} \right) – \left( \frac{4}{3}(0)^3 – 2(0)^2 + 0 \right) \)
\( A = \left( \frac{4}{3} \cdot \frac{1}{8} – 2 \cdot \frac{1}{4} + \frac{1}{2} \right) \)
\( A = \left( \frac{1}{6} – \frac{1}{2} + \frac{1}{2} \right) \)
\( A = \frac{1}{6} \)
So, the area of the shaded region is \( \frac{1}{6} \) square units.
Question
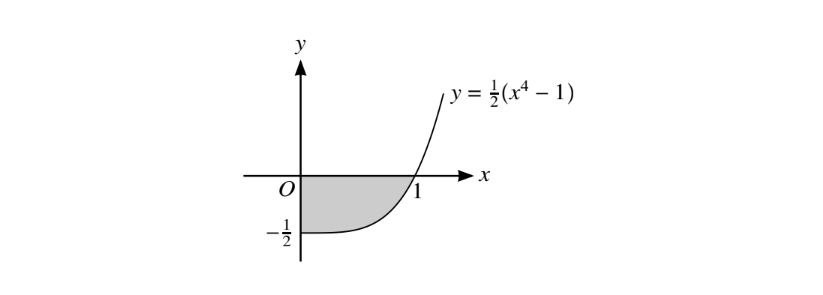
The diagram shows part of the curve \(y=\frac{1}{2}\left ( x^{4}-1 \right )\),defined for\( x\geq 0\)
(i)Find, showing all necessary working ,the area of shaded region.
(ii)Find, showing all necessary working, the volume obtained when the shaded region is rotated through \(360^{\circ}\) about the axis.
(iii)Find, showing all necessary working, the volume obtained when the shaded region is rotated through \(360^{\circ}\) about the y-axis.
Answer/Explanation
(i)Area=\(\int \frac{1}{2}\left ( x^{4} -1\right )dx=\frac{1}{2}\left [ \frac{x^{5}}{5} -x\right ]\)
\(\frac{1}{2}\left [ \frac{1}{5}-1 \right ]-0=-\left (\frac{2}{5} \right )\)
(ii)\(Vol=\pi \int y^{2}dx=\frac{1}{4}\int \left ( x^{8}-2x^{4}+1 \right )dx\)
\(\frac{1}{4}\left ( \pi \right )\left [ \frac{x^{9}}{9}-\frac{2x^{5}}{5}+x \right ]\)
\(\frac{1}{4}\left ( \pi \right )\left [ \frac{1}{9}-\frac{2}{5}+1 \right ]-0\)
\(\frac{8\pi }{45}\) or 0.559
(iii)\(Vol=\pi \int x^{2}dy=\left ( \pi \right )\int \left ( 2y+1` \right )^{\frac{1}{2}}dy\)
\(\pi \left [ \frac{\left ( 2y+1 \right )^{\frac{3}{2}}}{\frac{3}{2}} \right ]\left [ \div 2 \right ]\)
\(\left ( \pi \right )\left [ \frac{1}{3} -0\right ]\)
\(\frac{\pi }{3}\) or 1.05
Question
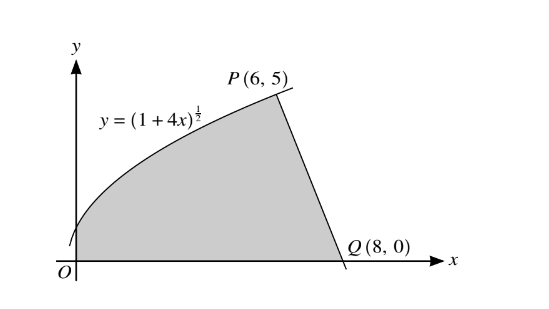
The diagram shows part of the curve \(\left ( 1+4x \right )^{\frac{1}{2}} \) and a point P (6, 5) lying on the curve. The line PQ intersects the x-axis at Q (8, 0).
(i) Show that PQ is a normal to the curve.
(ii) Find, showing all necessary working, the exact volume of revolution obtained when the shaded region is rotated through \(360^{\circ}\) about the x-axis. In part (ii) you may find it useful to apply the fact that the volume, V, of a cone of base radius r and vertical height h, is given by \(V=\frac{1}{3}\pi r^{2}h\).
Answer/Explanation
(i)\(\frac{\mathrm{d} y}{\mathrm{d} x}=\left [ \frac{1}{2}(1+4x)^{-\frac{1}{2}} \right ]\times 4\)
At x=6 ,\(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2}{5}
Gradient of PQ\(=-\frac{5}{2}\) hence PQ is a normal or \(m_{1}m_{2}=-1\)
(ii)Volume for curve=\(\pi \int (1+4x)\) and attempt to integrate \(y^{2}\)
\(=\pi \left [ x+2x^{2} \right ]\)
\(=\pi \left [ 6+72-0 \right ]\)
\(=78(\pi )\)
Vol for line \(=\frac{1}{3}\times \pi \times 5^{2}\times 2\)
\(=\frac{50}{3}\pi \)
Total volume \(=78\pi +\frac{50\pi }{3}=94\tfrac{2}{3}\pi \)
Question
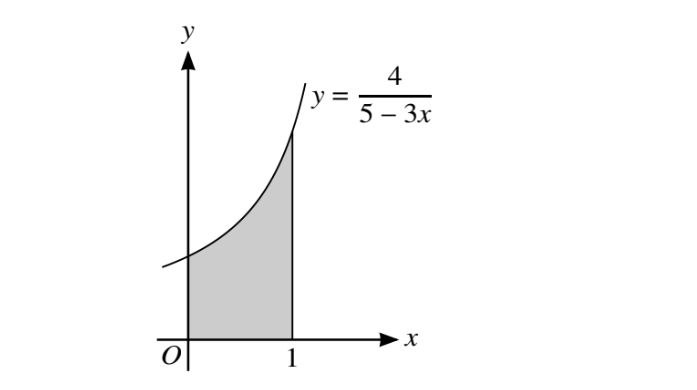
The diagram shows the part of the curve \(y=\frac{4}{5-3x}\)
(i)Find the equation of the normal to the curve at the curve at the point where x=1 in th e form y=mx+c,where m and c are constants.
The shaded region is bounded by the curve,the coordinate axes and the line x=1
(ii)Find, showing all the necessary w2orking,the volume obtained when this shaded region is rotated through \(360^{\circ}\) about the axis
Answer/Explanation
.(i) \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{4}{\left ( 5-3x \right )^{2}}\times \left ( -3 \right )\)
Gradient of tangent=3,Gradient of normal\(=\frac{1}{3}\)
→eqn:\(y-2=-\frac{1}{3}\left ( x-1 \right )\)
→\(y=-\frac{1}{3}x+\frac{7}{3}\)
(ii)Vol\(=\pi \int_{0}^{1}\frac{16}{\left ( 5-3x \right )^{2}}dx\)
\(\pi \left [ \frac{-16}{\left ( 5-3x \right )}\div -3 \right ]\)
\(\left ( \pi \left ( \frac{16}{6}-\frac{16}{15} \right ) \right )=\frac{8\pi }{5}\) (if limits switched must show – to +)
Question
Solve the equation \(3 sin^2\Theta = 4 cos \Theta -1\) for 0° < 0 ≤ 360°.
Answer/Explanation
\(3\sin ^{2}\Theta =4\cos \Theta -1\)
Uses \(s^{2}+c^{2}=1\)
\(\rightarrow 3c^{2}+4c-4\left ( =0 \right )\)
\(\left ( \rightarrow c=\frac{2}{3} or -2\right )\)
\(\rightarrow \Theta =48.2^{\circ}\) or \(311.8^{\circ}\)
0.841,5.44 rads,A1 only
\(\left ( 0.268\pi ,1.73\pi \right )\)
Question
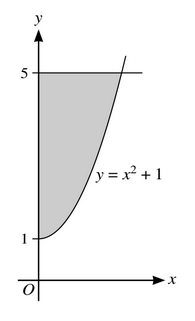
The diagram shows part of the curve with equation \(y=x^2+1\). The shaded region enclosed by the curve, the y-axis and the line y = 5 is rotated through \(360^0\) about the y-axis
Find the volume obtained.
Answer/Explanation
Ans:
\((\pi)\int (y-1)dy\)
\((\pi)[\frac{y^2}{2}-y]\)
\((\pi)[(\frac{25}{2}-5)-(\frac{1}{2}-1)]\)
\(8\pi\) or AWRT 25.1
Question.
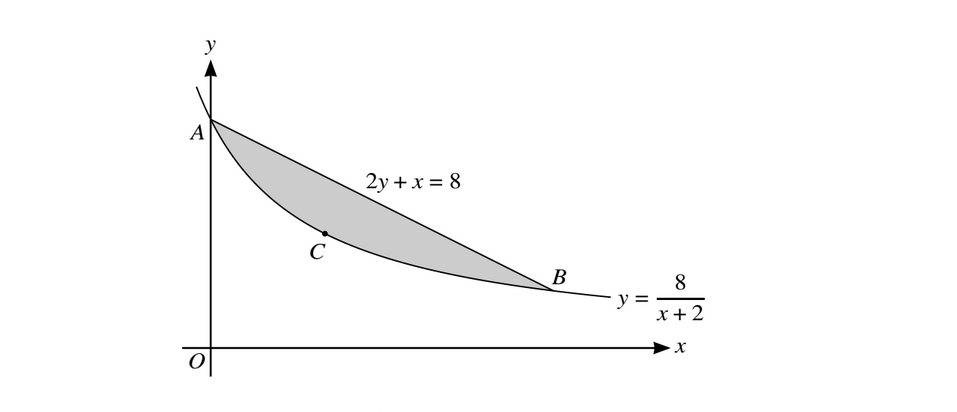
The diagram shows part of the curve \(y =\frac{8}{x+2}\) and the line \(2y + x = 8\), intersecting at points A and B. The point C lies on the curve and the tangent to the curve at C is parallel to AB.
(a) Find, by calculation, the coordinates of A, B and C.
(b) Find the volume generated when the shaded region, bounded by the curve and the line, is rotated through \(360^{\circ}\) about the x-axis.
Answer/Explanation
(a) Simultaneous equations \(\frac{8}{x+2}=4=\frac{1}{2}x\)
x = 0 or x = 6→ A (0, 4) and B (6, 1)
At \(C=\frac{-8}{(x+2)^{2}}=-\frac{1}{2}\rightarrow C(2,2)\)
(B1 for the differentiation. M1 for equating and solving)
(b) Volume under line \(\pi \int (-\frac{1}{2}x+4)^{2}dx=\left [ \frac{x^{3}}{12}-2x^{2}+16x \right ]=(42\pi )\)
(M1 for volume formula. A2,1 for integration)
Volume under curve \(=\pi \int \left ( \frac{8}{x+2} \right )^{2}dx=\pi \left [ \frac{-64}{x+2} \right ]=(24\pi )\)
Subtracts and uses 0 to 6→ 18π