Question
(a) Find the quotient when \(4x^3+17x^2+9x\) is divided by \(x^2+5x+6\), and show that the remainder is 18.
(b) Hence sole the equation \(4x^3+17x^2+9x-18=0\).
Answer/Explanation
Ans:
(a) Carry out division as far as 4x + k
Obtain quotient 4x – 3
Confirm remainder is 18
(b) State or imply equation is \((4x-3)(x^2+5x+6)=0\)
Attempt solution of cubic equation to find three real roots
Obtain \(-3,-2,\frac{3}{4}\)
Question
The polynomial p (x) is defined by
\(p(x)=x^{3}+ax^{2}+bx+16,\)
where a and b are constants. It is given that (x + 2) is a factor of p (x) and that the remainder is 72
when p(x) is divided by (x − 2).
Find the values of a and b
Answer/Explanation
Ans
Substitute x=−2 and equate to zero
Substitute x = 2 and equate to 72
Obtain 4 2 80 a b − += and 4 2 48 0 a b +−= or equivalents
Solve a pair of relevant linear simultaneous equations
Obtain a b = = 5, 14
Question
The polynomial p(x) is defined by
p(x) = ax3 − 11x2 − 19x − a,
where a is a constant. It is given that (x − 3) is a factor of p(x).
(a) Find the value of a. [2]
(b) When a has this value, factorise p(x) completely [3]
(c) Hence find the exact values of y that satisfy the equation p(ey + e−y)= 0. [4]
Answer/Explanation
Ans
7(a) Substitute x = 3 , equate to zero and attempt solution
Obtain a= 6
7 (b) Divide by x− 3 at least as far as the x term
Obtain 2 6 72 x x + + A1
Conclude (x- 3)(3x+ 2)(2x- 1)
7(c) Equate ey + e−y to positive value resulting from part (b)
Multiply by ey and use quadratic formula
Obtain \(e^{y}=\frac{3\pm \sqrt{5}}{2}\)
Obtain \(ln\frac{3\pm \sqrt{5}}{2}\)
Question
The polynomials f (x) and g(x) are defined by
f(x) = 4x3 + ax2 + 8x + 15 and g(x) = x2 + bx + 18,
where a and b are constants.
(a)Given that (x + 3) is a factor of f(x), find the value of a.
(b)Given that the remainder is 40 when g(x) is divided by (x – 2), find the value of b.
(c) When a and b have these values, factorise f(x) – g(x) completely.
Answer/Explanation
(a)Substitute x = −3, equate to zero and attempt solution for a
Obtain a =13
(b)Substitute x=2 , equate to 40 and attempt solution for b
Obtain b = 9
(c)Identify x + 3 as factor of f(x) – g(x)
Attempt, by division or equivalent, to find quadratic factor
Obtain (x + 3) (2x – 1) (2x +1)
Question
The polynomial p(x )s defined by \(p(x)=5x^{3}+ax^{2}+bx-16\),
where a and b are constants. It is given that(x − 2) is a factor of p(x) and that the remainder is 27 when p(x )is divided by (x + 1).
(i) Find the values of a and b.
(ii) Hence factorise p(x)completely.
Answer/Explanation
<p(1)Substitute x=2 and equate to zero
Substitute x=-1 and equate to 27
Obtain 4a+2b=-24 and a-b=48 or equivalents
Solve q relevant pair of simultaneous linear equations
Obtain a=12 ,b=-36
(ii)
Divide by x-2 at least as far as the term x term to obtain \(5x^{2}+\)(their a+10)x….
Obtain \(5x^{2}+22x+8\)
Obtain (x-2)(5x+2)(x+4)
Question
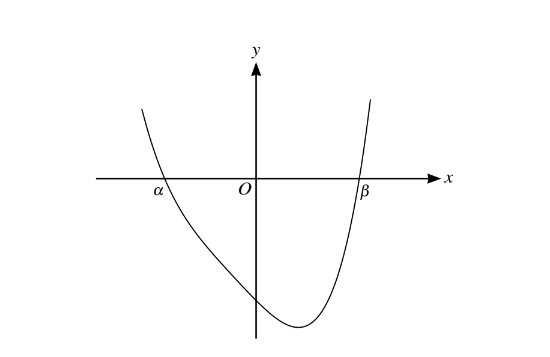
The diagram shows the curve with equation
\(y=x^{4}+2x^{3}+2x^{2}-12x-32\)
The curve crosses the x-axis at points with coordinates (\alpha ,0)(\beta ,0).
(i) Use the factor theorem to show that (x + 2 )is a factor of \(y=x^{4}+2x^{3}+2x^{2}-12x-32\)
(ii) Show that \(\beta\) satisfies an equation of the form x=\(\sqrt[3]{(p+qx)}\)and state the values of p and q.
(iii) Use an iterative formula based on the equation in part (ii) to find the value of\( \beta\)correct to4 significant figures. Give the result of each iteration to 6 significant figures.
Answer/Explanation
4(i) Substitute –2 and simplify
Obtain 16 -16 8 +24 -32 −and hence zero and conclude
4(ii) Attempt division by
x+2 to reach at least partial quotient\( x^{3}+kx\)or use of identity or inspection
Obtain\( x^{3}+2x-16\) Equate to zero and obtain x=\(\sqrt[3]{16-2x}\)
4(iii) Use iteration process correctly at least once
Obtain final answer 2.256
Show sufficient iterations to 6 sf to justify answer or show a sign change in the interval (2.2555, 2.2565)
Question
The polynomial p(x )is defined by\( p(x)=ax^{3}+ax^{2}-15x-18,\)
where a is a constant. It is given that(x − 2 )is a factor of p (x).
(i) Find the value of a. [2]
(ii) Using this value of a, factorise p(x )completely . [3]
(iii) Hence solve the equation \(p(e\sqrt{y})=0\) = 0, giving the answer correct to 2 significant figures.
Answer/Explanation
(i) Use quotient rule or equivalent
Obtain correct \(\frac{\frac{5}{x}(2x+1)-10Inx}{(2x+1)^{2}}\) or \(equivalent, or \frac{5}{x}(2x+1)^{-1}-10 Inx (2x+1)^{-2}\) or equivalent
Substitute x =1 to obtain \(\frac{15}{9}or \frac{5}{3}\) or equivalent, www
4(ii) Equate numerator to zero and attempt relevant arrangement
Confirm \(x=\frac{x+0.5}{Inx}\)
4(iii) Use iteration process correctly at least once
Obtain final answer 3.181
Show sufficient iterations to 6 sf to justify answer or show sign change in interval (3.1805, 3.1815)
Question
(i) Find the quotient when \(4x^{3}+8x^{2}11x+9\) is divided by( 2x + 1), and show that the remainder is 5.
(ii) Show that the equation \(4x^{3}+8x^{2}11x+4\) = 0 has exactly one real root
Answer/Explanation
.
4(i) Carry out division at least as far as \(2x^{2}+kx\)
Obtain quotient \(2x^{2}+3x+4\)
Confirm remainder is 5
4(ii) State or imply equation is \((2x+1)(2x^{2}+3x+4)=0\)
Calculate discriminant of 3-term quadratic expression or equivalent
Obtain –23 or equiv and conclude appropriately
Question
The polynomial p(x )is defined by\( p(x)=ax^{3}+bx^{2}-17x-a\)
where a and b are constants. It is given that(x + 2 )is a factor of p(x )and that the remainder is 28 when p
(x )is divided by (x − 2).
(i) Find the values of a and b.
(ii) Hence factorise p(x )completely.
(iii) State the number of roots of the equation \(p(2^{y})=0\),justifying your answer.
Answer/Explanation
(i) Substitute x = –2 and equate to zero
Substitute x = 2 and equate to 28
Obtain -9a+4b+34=0and 7a+4b-62=0 or equivalents
Solve a relevant pair of simultaneous equations for a or b
Obtain a = 6, b = 5
(ii) Divide by x + 2, or equivalent, at least as far as \(k^{1}x^{2}+k_{2}x\)
Obtain\( 6x^{2}-7x-3\)
Obtain (x+2)(3x+1)(3x-3)
(iii) Refer to, or clearly imply, fact that\( 2^{y}\) is positive State one
Question
The polynomial (x )is defined by
\(p(x)=8x^{3}+30x^{2}+13x-25\).
(i) Find the quotient when p(x) is divided by (x + 2), and show that the remainder is 5.
(ii) Hence factorise p(x − 5) completely.
(iii) Write down the roots of the equation p(|x| − 5) = 0.
Answer/Explanation
(i) Carry out division, or equivalent, at least as far as \(8x^{2}+kx\)
Obtain correct quotient \(8x^{2}+14x-15\)
Confirm remainder is 5
(ii) State or imply expression is(x+2)(….their quadratic quotient…)
Attempt factorisation of their quadratic quotient
Obtain (x+2)(2x+5)(4x-3)
(iii) State\( \pm \frac{3}{4}\) and no others, following their 3 linear factors
Question
(i) Find the quotient and remainder when
x4 + x3 + 3x2 + 12x + 6
is divided by (x2 − x + 4). [4]
(ii) It is given that, when
x4 + x3 + 3x2 + px + q
is divided by (x2 − x + 4), the remainder is zero. Find the values of the constants p and q. [2]
(iii) When p and q have these values, show that there is exactly one real value of x satisfying the equation
x4 + x3 + 3x2 + px + q = 0
and state what that value is. [3]
Answer/Explanation
Ans:
6 (i) Carry out division at least as far as quotient x2 + kx
Obtain partial quotient x2 + 2x
Obtain quotient x2 + 2x + 1 with no errors seen
Obtain remainder 5x + 2
(ii) Either Carry out calculation involving 12x + 6 and their remainder ax + b
Obtain p = 7, q = 4
Or Multiply x2 – x + 4 by their three-term quadratic quotient M1
Obtain p = 7, q = 4
(iii) Show that discriminant of 4x2 – x + 4 is negative
Form equation (x2 – x + 4)(x2 + 2x + 1) = 0 and attempt solution M1
Show that x2 + 2x + 1 = 0 gives one root x = −1
Question
The polynomial \(ax^{3}-5x^{2}+bx+9\) where a and b are constants, is denoted by p(x). It is given that (2x + 3) is a factor of p(x), and that when p(x) is divided by (x + 1) the remainder is 8.
(i) Find the values of a and b.
(ii) When a and b have these values, factorise p(x) completely.
Answer/Explanation
i) Substitute \(x=-\frac{3}{2}\) equate to zero
Substitute x = −1 and equate to 8
Obtain a correct equation in any form A1
Solve a relevant pair of equations for a or for b
Obtain a = 2 and b = −6
(ii)Attempt either division by 2x + 3 and reach a partial quotient of \(x^{2}+kx\), use of an identity or observation
Obtain quotient \(x^{2}-4x+3\)
Obtain linear factors x – 1 and x – 3
[Condone omission of repetition that 2x + 3 is a factor.]
[If linear factors x – 1, x − 3 obtained by remainder theorem or inspection, award B2 + B1]
Question
(i) The polynomial \(x^{3}+ax^{2}+bx+8\), where a and b are constants, is denoted by p(x). It is given that when p(x) is divided by x − 3 the remainder is 14, and that when p(x) is divided by x + 2 the remainder is 24. Find the values of a and b.
(ii) When a and b have these values, find the quotient when p(x) is divided by \(x^{2}+2x-8\) and hence solve the equation p(x)= 0.
Answer/Explanation
(i) Substitute x = 3 and equate to 14 ( ) 9a + 3b + 35 =14
Substitute x = −2 and equate to 24 ( ) 4a − 2b = 24
Obtain a correct equation in any form
Solve a relevant pair of equations for a or for b
Obtain a = 1 and b = −10
(ii)Attempt division by \(x^{2}+2x-8\) and reach a partial quotient of x – k
Obtain quotient x – 1 with no errors seen (can be done by observation) A1
Correct solution method for quadratic e.g. factorisation
All solutions x = 1, x = 2 and x = –4 given and no others CWO
Question
The polynomial \(ax^{3}-5x^{2}+bx+9\) where a and b are constants, is denoted by p(x). It is given that (2x + 3) is a factor of p(x), and that when p(x) is divided by (x + 1) the remainder is 8.
(i) Find the values of a and b.
(ii) When a and b have these values, factorise p(x) completely.
Answer/Explanation
i) Substitute \(x=-\frac{3}{2}\) equate to zero
Substitute x = −1 and equate to 8
Obtain a correct equation in any form A1
Solve a relevant pair of equations for a or for b
Obtain a = 2 and b = −6
(ii)Attempt either division by 2x + 3 and reach a partial quotient of \(x^{2}+kx\), use of an identity or observation
Obtain quotient \(x^{2}-4x+3\)
Obtain linear factors x – 1 and x – 3
[Condone omission of repetition that 2x + 3 is a factor.]
[If linear factors x – 1, x − 3 obtained by remainder theorem or inspection, award B2 + B1]
Question
The polynomial p(x) is defined by \(p(x)=ax^{3}-3x^{2}-5x+a+4\) ,where a is a constant.
(i) Given that (x − 2) is a factor of p(x), find the value of a.
(ii) When a has this value,
(a) Factorise p(x) completely.
(b) find the remainder when p(x) is divided by (x + 1).
Answer/Explanation
(i) Substitute 2 and equate to zero or divide and equate remainder to zero
Obtain a = 2
(ii) (a) Attempt to find quadratic factor by division, inspection or identity
Obtain \(2x^{2}+x-3\)
Conclude (x – 2)(2x + 3)(x – 1)
(b) Attempt substitution of –1 or attempt complete division by x + 1
Obtain 6
Question
The polynomial \(2x^{3}-4x^{2}+ax+b\), where a and b are constants, is denoted by p(x). It is given that when p(x) is divided by (x + 1) the remainder is 4, and that when p(x) is divided by (x − 3) the remainder is 12.
(i) Find the values of a and b.
(ii) When a and b have these values, find the quotient and remainder when p(x) is divided by \((x^{2}-2)\).
Answer/Explanation
(i) Substitute x = −1, equate to zero and obtain a correct equation in any form
Substitute x = 3 and equate to 12
Obtain a correct equation in any form
Solve a relevant pair of equations for a or for b
Obtain a = −4 and b = 6 A1
(ii) Attempt division by \(x^{2}-k\) and reach a partial quotient of 2x − k
Obtain quotient 2x − 4
Obtain remainder −2