Question
Given that
ln (2x + 1) − ln (x − 3) = 2,
find x in terms of e. [4]
Answer/Explanation
Ans
Use correct logarithm property to simplify left-hand side
Use correct process to obtain equation without logarithms
Obtain \(\frac{2x+1}{x-3}=e^{2}\)
Obtain \(x=\frac{3e^{2}+1}{e^{2-2}}\)
Question
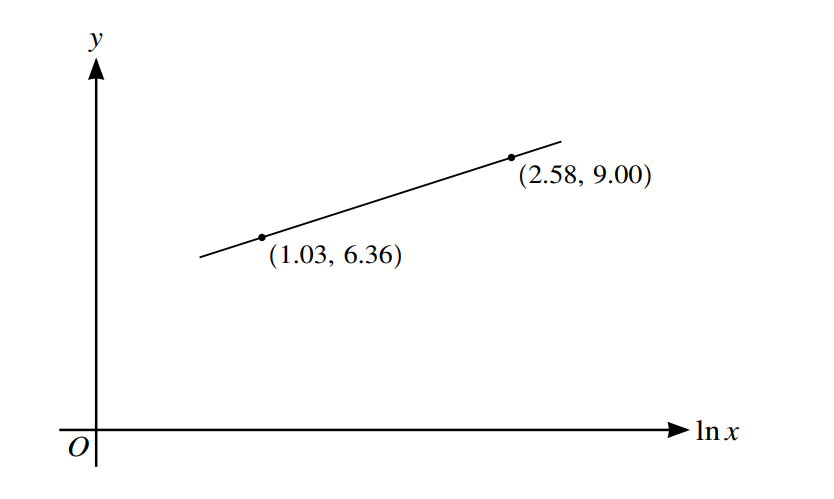
The variables x and y satisfy the equation ay = kx, where a and k are constants. The graph of y against ln x is a straight line passing through the points (1.03, 6.36) and (2.58, 9.00), as shown in the diagram.
Find the values of a and k, giving each value correct to 2 significant figures.
Answer/Explanation
Ans:
State or imply equation is y ln a = ln k + ln x
Equate gradient of line to \(\frac{1}{ln a}\)
Obtain \(\frac{1}{ln a}\) = \(\frac{2.64}{1.55}\) or equivalent and hence a =1.8
Substitute appropriate values to find ln k
Obtain ln 2.7… k = and hence k =15
Question
A curve has equation y = 7 + 4 ln (2x + 5)
Find the equation of the tangent to the curve at the point (-2, 7), giving your answer in the form y = mx + c.
Answer/Explanation
Ans:
Differentiate to obtain form \(\frac{k}{2x+5}\)
Obtain correct \(\frac{8}{2x+5}\)
Substitute x = − 2 to obtain gradient 8
Attempt equation of tangent through ((-2, 7) with numerical gradient
Obtain y= 8x + 23
Question
The polynomial p(x )is defined by \(p(x)=ax^{3}+ax^{2}-15x-18\), where a is a constant. It is given that(x − 2 )is a factor of p(x).
(i) Find the value of a.
(ii) Using this value of a, factorise p(x )completely.
(iii) Hence solve the equation \(p(e\sqrt{y})=0,\) giving the answer correct to 2 significant figures.
Answer/Explanation
[2]
4(i) Substitute x = 2 , equate to zero and attempt solution
Obtain a = 4
4(ii) Divide by x − 2 at least as far as the x term
Obtain\( 4x^{2}+12x+9\)
Conclude\( (x-2 (2x+3)^{2}\)
4(iii) Attempt correct process to solve \(e^{\sqrt{y}} \)= k where k >0
Obtain 0.48 and no others
Question
(i) Solve the inequality 2x − 7 < 2x − 9.
(ii) Hence find the largest integer n satisfying the inequality 2 ln n − 7 < 2 ln n − 9.
Answer/Explanation
1(i) State or imply non-modular inequality \((2x-7)^{2}<(2x-9)^{2}\)or corresponding equation or linear equation (with signs of 2x different)Obtain critical value 4 State x<4 only
1(ii) Attempt to find n from ln n = their critical value from part (i)
Obtain or imply n< \(e^{4}\) and hence 54
Question
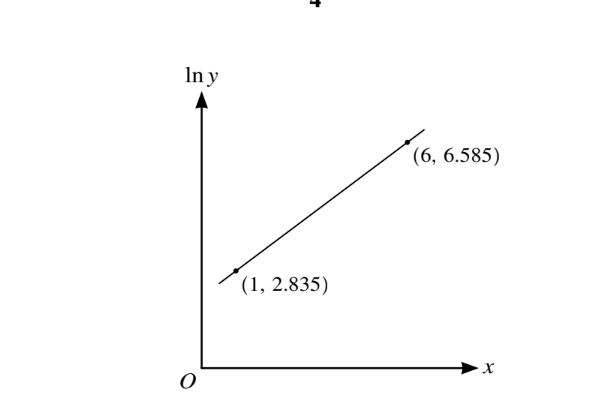
The variables x and y satisfy the equation \(y=Ae^{px+p}\) where A and p are constants. The graph of
ln y against x is a straight line passing through the points (1, 2.835 )and
(6, 6.585), as shown in the
diagram. Find the values of A and p.
Answer/Explanation
State or imply equation is ln ln y= A+ px+ p
Equate gradient of line to p
Obtain p = 0.75
Substitute appropriate values to find ln A
Obtain ln 1.335… A = and hence A= 3.8
Question
Solve the equation 2 ln
(2x )− ln(x + 3 )= ln(3x + 5).
Answer/Explanation
Use 2In(2x)=In\( (2x)^{2}\) Use addition or subtraction property of logarithms
Obtain \(4x^{2}=(x+3)(3x+5) \) or equivalent without logarithms
Solve 3-term quadratic equation
Conclude with x = 15 only
Question
It is given that k is a positive constant. Solve the equation 2 ln x = ln(3k + x) + ln(2k − x), expressing x in terms of k. [5]
Answer/Explanation
Ans:
Use 2ln x = ln x2
Use law for addition or subtraction of logarithms
Obtain x2 = (3 + x) (2-x) or equivalent with no logarithms
Solve 3-term quadratic equation
Obtain \(x\frac{3}{2}\) and no other solutions
Question
Use logarithms to solve the equation
5x+3 = 7x-1,
giving the answer correct to 3 significant figures. [4]
Answer/Explanation
Ans:
Introduce logarithms and use power law twice
Obtain (x + 3)log 5 = (x −1)log 7 or equivalent
Solve linear equation for x
Obtain 20.1
Question
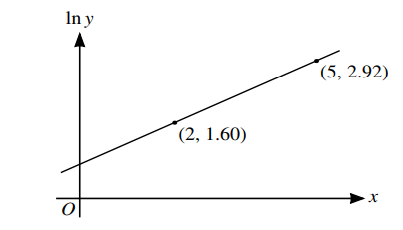
The variables x and y satisfy the equation
y = Aep(x−1),
where A and p are constants. The graph of ln y against x is a straight line passing through the points (2, 1.60) and (5, 2.92), as shown in the diagram. Find the values of A and p correct to 2 significant figures. [5]
Answer/Explanation
Ans:
2 State or imply that ln y = ln A + p(x-1)
Equate gradient to p or obtain two equations for ln A and p
Obtain p = 0.44
Substitute values correctly, to find value of ln A
Obtain A = 3.2
Alternative:
Obtain an equation either e1.6 = Aep or e2.92 = Ae4p
Obtain both equations correctly
Solve to obtain p = 0.44
Substitute value correctly to find A
Obtain A = 3.2
Question
Solve the equation \(\ln (3-2x))-2\ln x=\ln 5\).
Answer/Explanation
Use \(2\ln x=\ln (x^{2})\)
Use law for addition or subtraction of logarithms
Obtain correct quadratic equation in x A1
Make reasonable solution attempt at a 3-term quadratic
(dependent on previous M marks)
State \(x=\frac{3}{5}\) and no other solutions
Question
Use logarithms to solve the equation \(5^{x}=3^{2x-1}\), giving your answer correct to 3 significant figures.
Answer/Explanation
Use law for the logarithm of a product, a quotient or a power
Obtain \(x\log 5=(2x-1)\log 3\) or equivalent
Solve for x
Obtain answer x = 1.87
Question
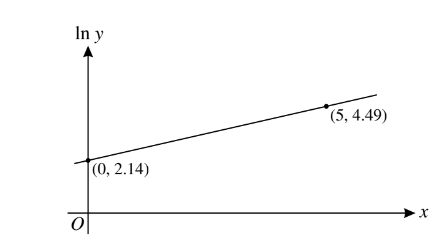
The variables x and y satisfy the equation \((y=A(b^{x})\) ,where A and b are constants. The graph of ln y against x is a straight line passing through the points (0, 2.14) and (5, 4.49), as shown in the diagram.
Find the values of A and b, correct to 1 decimal place.
Answer/Explanation
State or imply that \(\ln y=\ln A+x\ln b\)
Equate intercept on y-axis to \(\ln A\)
Obtain \(\ln A=2.14\) and hence A=8.5
Attempt gradient of line or equivalent (or use of correct substitution)
Obtain 0.47= or equivalent and hence b=1.6
Question
(a) Find \(\int \frac{1+Cos^{4}2x}{cos^{2}2x}\)
(b) Without using a calculator, find the exact value of dx, giving your answer in the form ln , where a and b are integers
Answer/Explanation
.
Question
It is given that k is a positive constant. Solve the equation 2 ln x = ln(3k + x) + ln(2k − x), expressing x in terms of k. [5]
Answer/Explanation
Ans:
Use 2ln x = ln x2
Use law for addition or subtraction of logarithms
Obtain x2 = (3 + x) (2-x) or equivalent with no logarithms
Solve 3-term quadratic equation
Obtain \(x\frac{3}{2}\) and no other solutions
Question
Use logarithms to solve the equation
5x+3 = 7x-1,
giving the answer correct to 3 significant figures. [4]
Answer/Explanation
Ans:
Introduce logarithms and use power law twice
Obtain (x + 3)log 5 = (x −1)log 7 or equivalent
Solve linear equation for x
Obtain 20.1
Question

The variables x and y satisfy the equation
y = Aep(x−1),
where A and p are constants. The graph of ln y against x is a straight line passing through the points (2, 1.60) and (5, 2.92), as shown in the diagram. Find the values of A and p correct to 2 significant figures. [5]
Answer/Explanation
Ans:
2 State or imply that ln y = ln A + p(x-1)
Equate gradient to p or obtain two equations for ln A and p
Obtain p = 0.44
Substitute values correctly, to find value of ln A
Obtain A = 3.2
Alternative:
Obtain an equation either e1.6 = Aep or e2.92 = Ae4p
Obtain both equations correctly
Solve to obtain p = 0.44
Substitute value correctly to find A
Obtain A = 3.2
Question
Solve the equation \(\ln (3-2x))-2\ln x=\ln 5\).
Answer/Explanation
Use \(2\ln x=\ln (x^{2})\)
Use law for addition or subtraction of logarithms
Obtain correct quadratic equation in x A1
Make reasonable solution attempt at a 3-term quadratic
(dependent on previous M marks)
State \(x=\frac{3}{5}\) and no other solutions
Question
Use logarithms to solve the equation \(5^{x}=3^{2x-1}\), giving your answer correct to 3 significant figures.
Answer/Explanation
Use law for the logarithm of a product, a quotient or a power
Obtain \(x\log 5=(2x-1)\log 3\) or equivalent
Solve for x
Obtain answer x = 1.87
Question

The variables x and y satisfy the equation \((y=A(b^{x})\) ,where A and b are constants. The graph of ln y against x is a straight line passing through the points (0, 2.14) and (5, 4.49), as shown in the diagram.
Find the values of A and b, correct to 1 decimal place.
Answer/Explanation
State or imply that \(\ln y=\ln A+x\ln b\)
Equate intercept on y-axis to \(\ln A\)
Obtain \(\ln A=2.14\) and hence A=8.5
Attempt gradient of line or equivalent (or use of correct substitution)
Obtain 0.47= or equivalent and hence b=1.6
