Question
A curve is defined by the parametric equations
x = 3t − 2 sin t, y = 5t + 4 cos t,
where \(0\leqslant t\leqslant 2\pi \). At each of the points P and Q on the curve, the gradient of the curve is \(\frac{5}{2}\).
(a) Show that the values of t at P and Q satisfy the equation 10 cos t − 8 sin t = 5. [3]
(b) Express 10 cost − 8 sin t in the form \(R\cos (t+\alpha ), where \ R> 0> and \ 0< \alpha < \frac{1}{2}\pi \). Give the exact
value of R and the value of \(\alpha\) correct to 3 significant figures. [3]
(c) Hence find the values of t at the points P and Q. [4]
Answer/Explanation
Ans
(a) Carry out division at least as far as 3x2+ kx
Obtain quotient 3x2 – 4 – 4
Confirm remainder is 9 AG
(b) Integrate to obtain at least k1 x3 and k2 ln(3x + 2) terms
Obtain x3 – 2x2 – 4x + 3 ln(3x + 2)
(FT from quotient in part (a))
Apply limits correctly
Apply appropriate logarithm properties correctly
Obtain 125 ln64
(c) State or imply \(9x^{3}-6x^{2}-20x-8=(3x+2)(3x^{2}-4x-4) \)
(FT from quotient in part (a))
Attempt to solve cubic eqn to find positive value of x (or of 3ey )
Use logarithms to solve equation of form 3ey = k where k > 0 M1
Obtain \(\frac{1}{3}ln2\) or exact equivalent
Question
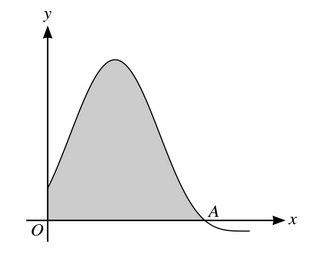
The diagram shows part of the curve with equation
\(y=4sin^2x+8sinx+3\).
where x is measured in radians. The curve crosses the x-axis at the point A and the shaded region is bounded by the curve and the lines x=0 and y=0.
(a) Find the exact x-coordinate of A.
(b) Find the exact gradient of the curve at A.
(c) Find the exact area of the shaded region.
Answer/Explanation
Ans:
(a) Solve equation y = 0 to find the value of x
Obtain \(\frac{7}{6}\pi\)
(b) Attempt first derivative using chain rule
Obtain \(\frac{dy}{dx}=8sinxcosx+8cos x\)
Substitute value from part (a) to find gradient \(-2\sqrt{3}\)
(c) Express integrand in the form \(k_1+k_2 cos 2x + k_3 sin x\)
Obtain correct 5 – 2cos 2x + 8sin x
Integrate to obtain 5x – sin2x – 8cos x
Apply limits 0 and their value from part (a) correctly
Obtain \(\frac{35}{6}\pi+\frac{7}{2}\sqrt{3}+8\) or exact equivalent
Question
A curve has equation
\(3x^2-y^2-4 In(2y+3)=26\).
Find the equation of the tangent to the curve at the point (3, -1).
Answer/Explanation
Ans:
Differentiate \(-y^2\) to obtain \(-2y\frac{dy}{dx}\)
Differentiate -4In(2y+3) to obtain \(\frac{-8}{2y+3}\frac{dy}{dx}\)
Attempt differentiation of all terms
Substitute x = 3, y =-1 to find numerical value of \(\frac{dy}{dx}\)
Obtain \(\frac{dy}{dx}=3\)
Obtain equation y = 3x – 10
Question
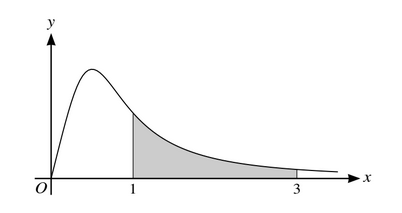
The diagram shows part of the curve with equation \(y=\frac{5x}{4x^3+1}\). The shaded region is bounded by the curve and the lines x=1, x=3 and y=0.
(a) Find \(\frac{dy}{dx}\) and hence find the the x-coordinate of the maximum point.
(b) Use the trapezium rule with two intervals to find an approximation to the area of the shaded region. Give your answer correct to 2 significant figures.
(c) State, with a reason, whether your answer to part (b) is an over-estimate or under-estimate of the exact area of the shaded region.
Answer/Explanation
Ans:
- Differentiate using quotient rule (or product rule)
Obtain \(\frac{5(4x^3+1)-60x^3}{(4x^3+1)^2}\)
Equate first derivative to zero and attempt solution
Obtain \(x=\frac{1}{2}\) - Use y values \(\frac{5}{5}, \frac{10}{33}, \frac{15}{109}\) or decimal equavalents
Use correct formula, or equivalent, with h=1
Obtain \(\frac{1}{2}(1+\frac{20}{30}+\frac{15}{109})\) or equivalent and hence 0.87 - State over-estimate with reference to top of each trapezium above curve
Question
The parametric equations of a curve are
\(x=e^{2t}cos4t\), y=3sin2t.
Find the gradient of the curve at the point for which t=0.
Answer/Explanation
Ans:
Attempt use of product rule to find \(\frac{dx}{dt}\)
Obtain \(2e^{2t}cos4t-4e^{2t}sin 4t\)
Obtain \(\frac{dy}{dt}=6cos2t\)
Divide to find \(\frac{dy}{dx}\) with t = 0 substituted
Obtain 3
Question
A curve has equation \(y=f(x) \ where \ f(x)=\frac{4x^{3}+8x-4}{2x-1}\)
(a) Find an expression for\(\frac{dy}{dx}\) and hence find the coordinates of each of the stationary points of the
curve \(y=f(x)\) [5]
(b) Divide \(4x^{3}+8x-4 \ by \ (2x-1), \ and \ hence \ find \ \int f(x)dx\) [5]
Answer/Explanation
Ans
8(a) Differentiate using the quotient rule (or product rule)
Obtain \(\frac{(2x-1)(12x^{3}+8)-2(4x^{3}+8x-4)}{(2x-1)^{2}}\)
Equate first derivative to zero and attempt solution
Obtain (0, 4)
Obtain \(\left ( \frac{3}{4},\frac{59}{8} \right )\)
8 (b) Carry out division to obtain quotient of form 2x2 + kx + m
Obtain correct quotient \(2x^{2}+x+\frac{9}{2}\)
Obtain remainder \(\frac{1}{2}\)
Integrate to obtain at least \(k_{1}x^{3}\ and \ k_{2} \ ln(2x-1) \ terms\)
Obtain \(\frac{2}{3}x^{3}+\frac{1}{2}x^{2}+\frac{9}{2}x+\frac{1}{4}ln(2x-1)\) as final answer
Question
A curve is defined by the parametric equations
x = 3t − 2 sin t, y = 5t + 4 cos t,
where 0 ≤ t ≤ 2π. At each of the points P and Q on the curve, the gradient of the curve is \(\frac{5}{2}\)
(a) Show that the values of t at P and Q satisfy the equation 10 cost − 8 sin t = 5. [3]
(b) Express 10 cost − 8 sin t in the form \(R \cos(t+\alpha ), \ where \ R> 0\ and \ 0< \alpha \frac{1}{2}\pi\). Give the exact
value of R and the value of \(\alpha \) correct to 3 significant figures. [3]
(c) Hence find the values of t at the points P and Q. [4]
Answer/Explanation
Ans
7 (a) Obtain \(\frac{dx}{dt}=3-2\cos t \ and \ \frac{dy}{dt}=5-4\sin t \)
Equate expression for \(\frac{dy}{dx}\ to \ \frac{5}{2}\)
Obtain \(10\cos t-8\sin t=5\)
7 (b) State \(R=\sqrt{164}\) or exact equivalent
Use appropriate trigonometry to find \(\alpha \)
Obtain 0.675 with no errors seen
7 (c) Carry out correct method to find one value of t
Obtain 0.495
Carry out correct method to find second value of t
Obtain 4.44
Question
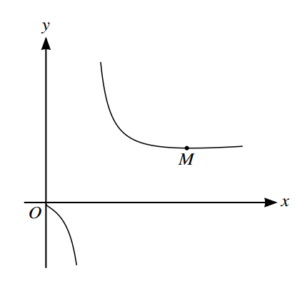
The diagram shows the curve with equation \(y=\frac{3x+2}{ln x} \). The curve has a minimum point M.
(a) Find an expression for \(\frac{dy}{dx}\) and show that the x-coordinate of M satisfies the equation \(x=\frac{3x+2}{3 lnx}\)
(b) Use the equation in part (a) to show by calculation that the x-coordinate of M lies between
3 and 4. [2]
(c) Use an iterative formula, based on the equation in part (a), to find the x-coordinate of M correct
to 5 significant figures. Give the result of each iteration to 7 significant figures. [3]
Answer/Explanation
Ans
5 (a) Use quotient rule (or equivalent) to find first derivative
Obtain \(\frac{dy}{dx}=\frac{3ln x-\frac{1}{x}(3x+2)}{(lnx)^{2}}\)
Equate first derivative to zero and confirm \(x=\frac{3x+2}{3lnx}\)
5 (b) Consider \(x-\frac{3x+2}{3lnx}\) or equivalent for values 3 and 4
Obtain −0.33… and 0.63… or equivalents and justify conclusion
5 (c) Use iteration process correctly at least once
Obtain final answer 3.3223
Show sufficient iterations to 7 s.f. to justify answer or show sign
change in the interval [3.32225, 3.32235]
Question
A curve has parametric equations
x = ln (2t + 6) − ln t, y = t ln t.
(a) Find the value of t at the point P on the curve for which x = ln 4. [3]
(b) Find the exact gradient of the curve at P. [5]
Answer/Explanation
Ans
4 (a) Equate x to ln 4 and use relevant logarithm property
Obtain equation with no logarithm present, \(\frac{2t+6}{t}=4\)
Obtain t = 3
4 (b) Obtain \(\frac{dx}{dt}=\frac{2}{2t+6}-\frac{1}{t}\)
Use product rule to find \(\frac{dy}{dt}\)
Obtain \(ln t+t\times \times \frac{1}{t}\)
Divide to obtain \(\frac{dy}{dx}\ using \ their\ \frac{dy}{dt}\ and \ \frac{dx}{dt}\ correctly\)
Obtain 6(ln3 1)
Question
. 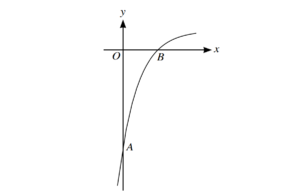
The diagram shows the curve with parametric equations
\(x = ln (2t + 3), y = \frac{2t-3}{2t+3}\)
The curve crosses the y-axis at the point A and the x-axis at the point B
Answer/Explanation
(a)Show that \(\frac{dy}{dx} = \frac{6}{2t + 3}\).
(b)Find the gradient of the curve at A.
(c) Find the gradient of the curve at B.(a)Obtain \(\frac{dy}{dt} = \frac{6}{2t + 3}\).
Use quotient rule, or equivalent, to find \(\frac{dy}{dt}\)
Obtain \(\frac{dy}{dt}\) = \(\frac{2(2t+3)-2(2t-3)}{(2t+3)^{2}}\)
Divide to confirm \(\frac{dy}{dx}\) = \(\frac{6}{2t+3}\)
(b)Attempt to find value of t corresponding to x=0
Obtain t = −1 and hence gradient is 6
(c)Attempt to find value of t corresponding to y=0
Obtain t = \(\frac{3}{2}\) and hence gradient is 1
Question
The curve with equation y = xe2x + 5e−x has a minimum point M.
(a)Show that the x-coordinate of M satisfies the equation x = \(\frac{1}{3}\) ln 5 − \(\frac{1}{3}\) ln (1 + 2x).
(b)Use an iterative formula, based on the equation in part (a), to find the x-coordinate of M correct to 3 significant figures. Use an initial value of 0.35 and give the result of each iteration to 5 significant figures.
Answer/Explanation
(a)Attempt use of product rule to differentiate xe2x
Obtain e2x + 2xe2x – 5e-x
Equate first derivative to zero and multiply by ex to obtain an equation involving e3x
Obtain e3x(1 + 2x) = 5 or equivalent
Confirm given result x = \(\frac{1}{3}\) ln5 – \(\frac{1}{3}\) ln (1 + 2x) with sufficient detail.
(b)Use iteration process correctly at least once
Obtain final answer 0.357
Show sufficient iterations to 5sf to justify answer or show sign change in interval [0.3565, 0.3575]
Question
A curve has equation e2xy – ey = 100.
(a)Show that \(\frac{dy}{dx}=\frac{2e^{2x}y}{e^{y-e^{2x}}}.\)
(b)Show that the curve has no stationary points.
It is required to find the x-coordinate of P, the point on the curve at which the tangent is parallel to the y-axis.
(c)Show that the x-coordinate of P satisfies the equation.
x = ln 10 \(-\frac{1}{2}In (2x-1)\)State or imply ey – e2x = 0 and hence y = 2x
(d)Use an iterative formula, based on the equation in part (c), to find the x-coordinate of P correct to 3 significant figures. Use an initial value of 2 and give the result of each iteration to 5 significant figures.
Answer/Explanation
(a)Use product rule to differentiate e2x y
Obtain \(2e^{2x}y+e^{2x}\frac{dy}{dx}\)
Obtain \(2e^{2x}y+e^{2x}\frac{dy}{dx}- e^{y}\frac{dy}{dx} = 0\) and rearrange to confirm given result.
(b)Consider e2xy = 0 and either state e2x ≠ 0 or substitute y = 0 in equation of curve
Complete argument with e2x ≠ 0 or e2x> 0 and substitution to show y cannot be zero.
(c)Substitute for y in equation of curve and attempt rearrangement as far as e2x = …..
Use relevant logarithm properties
Confirm equation \(x = In 10 – \frac{1}{2}In (2x-1)\)
(d)Use iteration process correctly at least once
Obtain final answer 1.82
Show sufficient iterations to 5 sf to justify answer or show sign change in interval [1.815, 1.825]
Question
(a)Given that y = \(tan^{2}x,\) show that \(\frac{dy}{dx} = 2 tan x + 2tan^{3}x.\)
(b)Find the exact value of \(\int_{\frac{1}{4}\pi }^{\frac{1}{3}\pi } \left ( tan x + tan^{2}x + tan^{3}x \right )dx\) .
Answer/Explanation
(a)Differentiate to obtain 2 tan x sec2 x
Use sec2 x = 1 + tan2 x to confirm 2 tan x + 2 tan3x
(b)Attempt to use part (a) result to integrate tan x + tan 3 x
Obtain \(\frac{1}{2}tan^{2}x\)
Use relevant identity to integrate tan2x
Obtain sec2 x−1 and hence tan x−x
Use limits correctly for integrand of form k1 tan2 x + k2 tan x + k3x
Obtain \(\sqrt{3} – \frac{1}{12}\pi \)
Question
(a)Show that sin 2θ cot θ − cos 2θ ≡ 1.
(bHence find the exact value of \(sin\frac{1}{6}\pi cot\frac{1}{12}\pi \).
(c) Find the smallest positive value of 1 (in radians) satisfying the equation
sin 2θ cotθ − 3 cos 2θ = 1.
Answer/Explanation
(a)Use at least two of sin 2θ = 2sin θ cos θ, cos 2θ = cos2θ – sin2θ, cotθ = \(\frac{cos\theta }{sin\theta }\)
Express LHS in terms of sin θ and cos θ only and attempt valid simplification
Obtain cos2 θ + sin2 θ or equivalent and hence 1
(b)Substitute θ = \(\frac{1}{12}\pi \) and show or imply \(sin\frac{1}{6}\pi cot\frac{1}{12}\pi = 1 + cos\frac{1}{6}\pi \)
Obtain 1+ \(\frac{1}{2}\sqrt{3}\) or exact equivalent
(c)Use the identity from part (a) to obtain − 2cos 2θ = 0 or equivalent
Obtain \(\theta = \frac{1}{4}\pi \)
Question
The variables x and y satisfy the equation y = 3 2a a x , where a is a constant. The graph of ln y against x is a straight line with gradient 0.239.
(a) Find the value of a correct to 3 significant figures.
(b)Hence find the value of x when y = 36. Give your answer correct to 3 significant figures.
Answer/Explanation
Ans:
(a)State or imply equation is ln y = ln 3 2a + x In a
Equate gradient of line involving a to 0.239
Obtain ln 0.239 a = and hence a =1.27
(b)Substitute y = 36 in ln y =… equation and solve for x
Obtain 3.32
Question
The equation of a curve is \(x^{2}-4xy-2y^{2}=1\)
(i)Find an expression for \(\frac{dy}{dx}\) and show that the gradient of the curve at the point(−1, 2) is-\(\frac{5}{2}\)
(ii) Show that the curve has no stationary points.
(iii) Find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y-axis
Answer/Explanation
.
7(i) Obtain\( -4y-4x\frac{dy}{dx}\)
from use of the product rule Differentiate \( -2y^{2} \)to obtain\( -4y\frac{dy}{dx}\)
Obtain 2 , 0 x = with no extra terms
Rearrange to obtain expression for\( \frac{dy}{dx}\) and substitute x = −1, y = 2
Obtain\( \frac{dy}{dx}=\frac{2x-4y}{4x+4y}\) OE and hence -\(\frac{5}{2}\)
7(ii) Equate numerator of derivative to zero to produce equation in x and y Substitute into equation of curve to produce equation in x or y
Obtain \(-6y^{2}=1 or -\frac{3}{2}x^{2}=1 \)
7(iii) Use denominator of derivative equated to zero with equation of curve to produce equation in x
Obtain \(3x^{2}=1 and hence x=\pm \frac{1}{\sqrt{3}}\)
Question
A curve has equation y =\(\frac{3+2Inx}{1+Inx}\).Find the exact gradient of the curve at the point for which y = 4.
Answer/Explanation
Use quotient rule (or product rule) to find first derivative Obtain\( -\frac{1}{x(1+Inx)^{2}}\) or (unsimplified) equivalent Use y=4 to obtain In\( x=-\frac{1}{2}\) or exact equivalent for x
Substitute for x in their first derivative
Obtain\( -4e^{\frac{1}{2}}\) or exact equivalent
Question
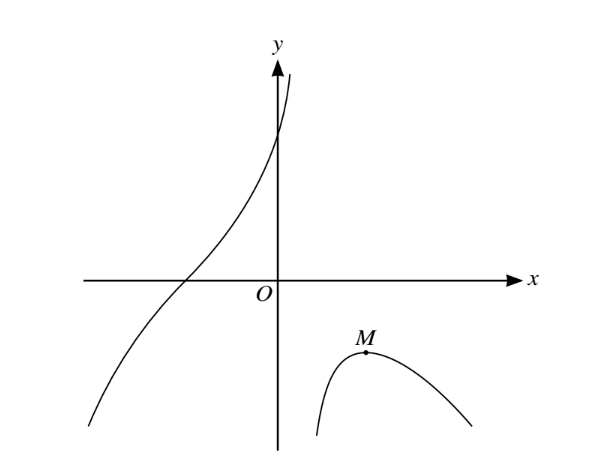
The diagram shows the curve with equation y=\(\frac{8+x^{3}}{2-5x}\).The maximum point is denoted by M.
(i) Find an expression for \(\frac{dy}{dx}\) and determine the gradient of the curve at the point where the curve crosses the x-axis.
(ii) Show that the x-coordinate of the point M satisfies the equation x =\(\sqrt{(0.6x+4x^{-1})}.\)
(iii) Use an iterative formula, based on the equation in part (ii), to find the x-coordinate of M correct to 3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
<p(i) Use quotient rule (or product rule) to differentiate .
Obtain \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{3x^{2}\left ( 2-5x \right )-\left ( -5 \right )\left ( 8+x^{3} \right )}{\left ( 2-5x \right )^{2}}\)
State or imply curve crosses x-axiz when x=-2.
Substitute -2 to obtain 1
(ii)Equate numerator of first derivative to zero and rearrange as far as \(kx^{3}\)=….or equivalent
Confirm given result \(x=\sqrt{0.6x+4x^{-1}}\)
(iii) Use iterative process correctly atleast once
Obtain final answer 1.81
Show sufficient iterations to 5sf to justify answer or show a sign change in the interval \(\left [ 1.805,1.815 \right ]\)
Question
Find the equation of the normal to the curve\(x^{2}In y+2x+5y\)=11
at the point(3, 1).
Answer/Explanation
Obtain \(2x\ln y+x^{2}\times \frac{1}{y}\times \frac{\mathrm{d} y}{\mathrm{d} x}\)
Obtain …..\(+2+5\frac{\mathrm{d} y}{\mathrm{d} x}=0\)
Substitute x=3 and y=1 to find value of their \(\frac{\mathrm{d} y}{\mathrm{d} x}\)
Obtain \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{2}{14}\)
Attempt equation of line through(3,1) with gradient of normal.
Obtain y=7x-20 or equivalent Unsimplified
Question
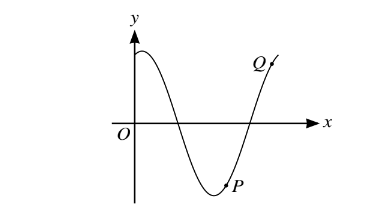
The diagram shows the curve with equation y = sin 2x + 3 cos 2x for 0 ≤ x ≤ 0. At the points P and Q on the curve, the gradient of the curve is 3.
(i) Find an expression for \(\frac{dy}{dx}\)
(ii) By first expressing \(\frac{dy}{dx}\) in the form R cos (2x + \alpha), where \(R>0 and 0<\alpha <\frac{1}{2}\pi\) R , find the x-coordinates of P and Q, giving your answers correct to 4 significant figures.
Answer/Explanation
7(i) State expression of form \(k_{1}cos2x+k_{2}sin2x\)
7(ii) State\( R=\sqrt{40} or 6.324…\)
Use appropriate trigonometry to find α
Obtain 1.249…
Equate their \(Rcos(2x+\alpha ) to 3 and find cos^{-1}(3\div R)\)
Carry out correct process to find one value of α
Obtain 1.979
Carry out correct process to find second value of α within the range
Obtain 3.055
Question
A curve has parametric equations.
x = t + ln (t + 1), \(y=3te^{2t}\)
(i) Find the equation of the tangent to the curve at the origin.
(ii) Find the coordinates of the stationary point, giving each coordinate correct to 2 decimal places.
Answer/Explanation
5(i) Use product rule to differentiate y obtaining \(k_{1}e^{2t}+k_{2}te^{2t}\)
Obtain correct \(3e^{2t}+6te^{2t}\)
State derivative of x is \(1+\frac{1}{t+1}\)
Use\( \frac{dy}{dx}=\frac{dy}{dt}/\frac{dx}{dt}\)
with t =0 to find gradient
Obtain\( y=\frac{3}{2}x\) or equivalent
5(ii) Equate\( \frac{dy}{dx} or \frac{dy}{dt}\) to zero and solve for t
Obtain\( t=-\frac{1}{2}\)
Obtain x =−1.19
Obtain y = −0.55
Question
The equation of a curve is \(x^{2} − 4xy − 2y^{2} = 1\).
(i) Find an expression for \(\frac{\mathrm{d}y }{\mathrm{d} x}\) and show that the gradient of the curve at the point \((−1, 2)\) is \( – \frac{5}{2}\).
(ii) Show that the curve has no stationary points.
(iii) Find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y-axis.
Answer/Explanation
(i) State \(R= \sqrt{29}\) or \(5.385…\)
Use appropriate trigonometry to find \(\alpha \)
Obtain \(0.3805\) with no errors seen
(ii)State that equation is \(5cos\Theta -2sin\Theta =4\)
Evaluate \(cos ^{-1} (k/R) – \alpha\) to find one value of θ
Obtain \( 0.353 \)
Carry out correct method to find second value
Obtain 5.17 and no extra solutions in the range.
(iii) State integrand as \(\frac{1}{29}sec^{2}(\frac{x}{2}+0.385)\)
Integrate to obtain from \(ktan(\frac{x}{2}+their\alpha )\)
Obtain \(\frac{2}{29}tan(\frac{x}{2}+0.385)+c\)
Question
The parametric equations of a curve are
x = 2t − sin 2t, y = 5t + cos 2t, for\( 0 ≤ t \frac{1}{2}\pi \) .
At the point P on the curve, the gradient of the curve is 2.
(i) Show that the value of the parameter at P satisfies the equation 2 sin 2t − 4 cos 2t = 1.
(ii) By first expressing 2 sin 2t − 4 cos 2t in the form\( R sin2t − \Theta\), where\( R > 0 and 0 < ! <\Theta\)
Answer/Explanation
(i) Obtain expression for \(\frac{dy}{dx}\) with numerator quadratic, denominator linear
Obtain\(\frac{3t^{2}-6t}{2t+4}\)
Identify t = 3 at P
Obtain \( \frac{9}{10}\)or equivalent
(ii) Equate first derivative to zero and obtain non-zero value of t
Obtain t = 2
Substitute to obtain (12,- 4)
(iii) Equate expression for gradient to m and rearrange to confirm\( 3t^{2}-(2m+6)-4m\)=0
Attempt solution of quadratic inequality or equation resulting from
discriminant
Obtain critical values -\(\sqrt{72}-9,m\geqslant \sqrt{72-9}\)
Conclude
\(m\leqslant \sqrt{72-9},m\geqslant \sqrt{72}-9\)
Question
The equation of a curve is \(y=\frac{e^{2x}}{4x+1}\) and the point P on the curve has y-coordinate 10.
(i) Show that the x coordinate of P satisfies the equation\( x=\frac{1}{2}In(40x+10).\)
(ii) Use the iterative formula \(x_{n+1}=\frac{1}{2}In(40x_{n}+10)with x_{1}= 2.3\) to find the x-coordinate of P correct
to 4 significant figures. Give the result of each iteration to 6 significant figures. [3]
(iii) Find the gradient of the curve at P, giving the answer correct to 3 significant figures.
Answer/Explanation
5(i) Attempt rearrangement of\( \frac{e^{2x}}{4x+1}=10 to x=….. \)involving ln
Confirm\( x=\frac{1}{2} In(40x+10)\)
5(ii) Use iteration process correctly at least once Obtain final answer 2.316 A1
Show sufficient iterations to 6 sf to justify answer or show a sign change in the interval [2.3155, 2.3165]
5(iii) Use quotient rule (or product rule) to find derivative Obtain \(\frac{2e^{2x}(4x+1)-4e^{2x}}{(4x+1)^{2}} \)or equivalent Substitute answer from part (ii) (or more accurate value) into attempt at first derivative Obtain 16.1
Question
Find the gradient of the curve \(x^{2}siny+cos3y=4\)
at the point\( (2,\frac{1}{2}\pi ).\)
Answer/Explanation
Use product rule for derivative of\( x^{2}sin y\)
Obtain\( 2xsiny +x^{2}cosy\frac{dy}{dx}\)
Obtain\( -3sin3y\frac{dy}{dx}\) as derivative of cos 3y
Obtain \(2xsiny+x^{2}cosy\frac{dy}{dx}-3sin3y\frac{dy}{dx}\)=0
Substitute\( x=2 y=\frac{1}{2}\pi \)to find value of \(\frac{dy}{dx}\)
Obtain\( -\frac{4}{3}\)
Question
The equation of a curve is y =\( \frac{3x^{2}}{x^{2}+4}\) At the point on the curve with positive x-coordinate p, the gradient of the curve is -\(\frac{1}{2}\)
(i) Show that p =\( \sqrt{\left ( \frac{48p-16}{p^{2}+8} \right )}\)
(ii) Show by calculation that 2 < p < 3.
(iii) Use an iterative formula based on the equation in part (i) to find the value of p correct to 4 significant figures. Give the result of each iteration to 6 significant figures
Answer/Explanation
.
(i) Use quotient rule or equivalent
Obtain or equivalent
Equate first derivative to and remove algebraic denominators dep on
Obtain or equivalent
Confirm given result
(ii) Consider sign of at 2 and 3 or equivalent
Complete argument correctly with appropriate calculations
(iii) Carry out iteration process correctly at least once Obtain final answer 2.728 Show sufficient iterations to justify accuracy to 4 sf or show sign change
in interval (2.7275, 2.7285)
Question
The equation of a curve is y =\( \frac{3x^{2}}{x^{2}+4}\) At the point on the curve with positive x-coordinate p, the gradient of the curve is -\(\frac{1}{2}\)
(i) Show that p =\( \sqrt{\left ( \frac{48p-16}{p^{2}+8} \right )}\)
(ii) Show by calculation that 2 < p < 3.
(iii) Use an iterative formula based on the equation in part (i) to find the value of p correct to 4 significant figures. Give the result of each iteration to 6 significant figures
Answer/Explanation
.
(i) Use quotient rule or equivalent
Obtain or equivalent
Equate first derivative to and remove algebraic denominators dep on
Obtain or equivalent
Confirm given result
(ii) Consider sign of at 2 and 3 or equivalent
Complete argument correctly with appropriate calculations
(iii) Carry out iteration process correctly at least once Obtain final answer 2.728 Show sufficient iterations to justify accuracy to 4 sf or show sign change
in interval (2.7275, 2.7285)
Question
A curve is defined by the parametric equations
\(x=2tan\Theta\) , \(y=3sin2\Theta\)
for \(0 ≤ \Theta <\frac{1}{2}\pi \)
(i) Show that\( \frac{dy}{dx}=6cos^{4}\Theta -3cos^{2}\Theta \)
(ii) Find the coordinates of the stationary point.
(iii) Find the gradient of the curve at the point \((2\sqrt{3},\frac{3}{2}\sqrt{3})\)
Answer/Explanation
(i) Obtain\( \frac{dx}{d\Theta }=2sec^{2}\Theta and \frac{dy}{d\Theta }=6cos2\Theta \)
Use\( cos2\Theta =2cos^{2}\Theta -1\) or equivalent
Form expression for \(\frac{dy}{dx} \) in terms of \(cos\Theta\)
Confirm\( 6cos^{4}\Theta -3cos^{2}\Theta\)with no errors seen
(ii) Equate first derivative to zero and obtain at least \(cos\Theta =\pm \frac{1}{\sqrt{2}} \)
Obtain\( \Theta =\frac{1}{4}\pi\) or equivalent
Obtain (2, 3)
(iii) State or imply \( \Theta =\frac{1}{3}\pi\) or equivalent
Obtain\( -\frac{3}{8}\) or equivalent only
Question
Find the gradient of the curve\(y=3e^{4x}-61 In(2x+3)\) at the point for which x = 0.
Answer/Explanation
Obtain first derivative of form \(k_{1}e^{4x}+\frac{k_{2}}{2x+3}\)
Obtain correct \(12e^{4x}+\frac{12}{2x+3}\)
Obtain 8
Question
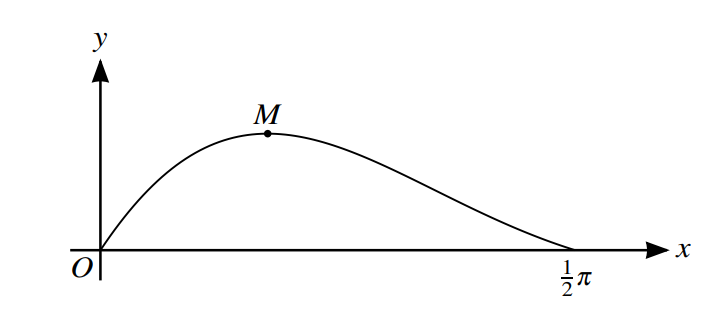
The diagram shows the part of the curve y = 3e−x sin 2x for \(0\leqslant x\leqslant \frac{1}{2}\pi \) , and the stationary point M.
(i) Find the equation of the tangent to the curve at the origin.[4]
(ii) Find the coordinates of M, giving each coordinate correct to 3 decimal places.[4]
Answer/Explanation
Ans:
6 (i) Use product rule to obtain expression of form \(k_{1}e^{-x}sin2x+k_{2}e^{-x}cos2x\)
Obtain correct \(-3e^{-x}sin2x+6e^{-x}cos2x\)
Substitute x = 0 in first derivative to obtain equation of form y = mx
Obtain y = 6x or equivalent with no errors in solution
(ii) Equate first derivative to zero and obtain tan 2x = k
Carry out correct process to find value of x
Obtain x = 0.554
Obtain y =1.543
Question
The equation of a curve is 2x3 + y3 = 24.
(i) Express \(\frac{dy}{dx}\) in terms of x and y, and show that the gradient of the curve is never positive.[4]
(ii) Find the coordinates of the two points on the curve at which the gradient is −2.[5]
Answer/Explanation
Ans:
7 (i) State \(3y^{2}\frac{dy}{dx}\) as derivative of y3
Equate derivative of left-hand side to zero and solve for \(\frac{dy}{dx}\)
Obtain \(\frac{dy}{dx}=-\frac{6x^{2}}{3y^{2}}\) or equivalent
Observe x2 and y2 never negative and conclude appropriately
(ii) Equate first derivative to −2 and rearrange to y2 = x2 or equivalent
Substitute in original equation to obtain at least one equation in x3 or y3
Obtain 3x3 = 24 or x3 = 24 or 3y3 = 24 or – y3 = 24
Obtain (2, 2)
Obtain \(\left ( \sqrt[3]{24},- \sqrt[3]{24}\right )\left ( \sqrt[3]{24},- \sqrt[3]{24}\right )\) − or (2.88, 2.88) − and no others
Question
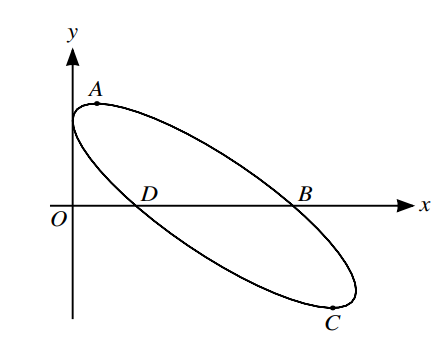
The parametric equations of a curve are
x = 6 sin2t, y = 2 sin 2t + 3 cos 2t,
for 0 ≤ t < π. The curve crosses the x-axis at points B and D and the stationary points are A and C, as shown in the diagram.
(i) Show that \(\frac{dy}{dx}=\frac{2}{3}\) cot 2t − 1. [5]
(ii) Find the values of t at A and C, giving each answer correct to 3 decimal places. [3]
(iii) Find the value of the gradient of the curve at B. [3]
Answer/Explanation
Ans:
7 (i) Obtain 12 sin t cos t or equivalent for \(\frac{dy}{dt}\)
Obtain 4 cos 2t − 6sin 2t or equivalent for \(\frac{dy}{dt}\)
Obtain expression for \(\frac{dy}{dx}\) in terms of t
Use 2sin t cos t = sin 2t
Confirm given answer \(\frac{dy}{dx}=\frac{2}{3}\) cot 2t − 1 with no errors seen
(ii) State or imply tan 2t \(=\frac{2}{3}\)
Obtain t = 0.294
Obtain t = 1.865
(iii) Attempt solution of 2sin 2t + 3cos 2t = 0 at least as far as tan 2t = …
Obtain tan 2t \(=-\frac{3}{2}\) or equivalent
Substitute to obtain \(-\frac{13}{9}\)
Question
A curve has equation
\(y=\frac{3x+1}{x-5}.\)
Find the coordinates of the points on the curve at which the gradient is −4. [5]
Answer/Explanation
Ans:
2 Use quotient rule or, after adjustment, product rule
Obtain \(\frac{3x-15-3x-1}{\left ( x-5 \right )^{2}}\) or equivalent
Equate first derivative to –4 and solve for x
Obtain x-coordinates 3 and 7 or one correct pair of coordinates
Obtain y-coordinates –5 and 11 respectively or other correct pair of coordinates
Question
The parametric equations of a curve are \(x=\cos 2\Theta -\cos \Theta ,y=4\sin ^{2}\Theta \)
,for \(0\leq \Theta \leq \pi \).
(i) Show that \( \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{8\cos \Theta }{1-4\cos \Theta }\).
(ii) Find the coordinates of the point on the curve at which the gradient is −4.
Answer/Explanation
(i) State \(\frac{\mathrm{d} x}{\mathrm{d} \Theta }=-2\sin 2\Theta +\sin \Theta \) or \(\frac{\mathrm{d} y}{\mathrm{d} \Theta }=8\sin 2\Theta \cos \Theta \)
Use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} \Theta }\div \frac{\mathrm{d} x}{\mathrm{d} \Theta }\).
Use sin 2θ = 2sinθ cosθ
Obtain given answer correctly
(ii) Equate derivative to −4 and solve for cos θ M1
Obtain cos θ = 1⁄2
Obtain x = −1
Obtain y = 3
Question
The parametric equations of a curve are
\(x=e^{2t},y=4te^{^{t}}\).
(i) Show that \( \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2(t+1)}{e^{t}}\)
(ii) Find the equation of the normal to the curve at the point where t = 0.
Answer/Explanation
(i) Use product rule to differentiate y M1
Obtain correct derivative in any form A1
Use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} t}\div \frac{\mathrm{d} x}{\mathrm{d} t}\)
Obtain given answer correctly.
(ii) Substitute t = 0 in \(\frac{\mathrm{d} y}{\mathrm{d} x}\) and both parametric equations
Obtain \(\frac{\mathrm{d} y}{\mathrm{d} x}=2\) and coordinates (1, 0) .
Form equation of the normal at their point, using negative reciprocal of their \(\frac{\mathrm{d} y}{\mathrm{d} x}\)
State correct equation of normal \(y=-\frac{1}{2}x+\frac{1}{2}\) or equivalent
Question
(i) By differentiating \(\frac{1}{\cos \Theta }\), show that if \(y=\sec \Theta \) then \(\frac{\mathrm{d} y}{\mathrm{d} \Theta }=\tan \Theta \sec \Theta \).
(ii)Hence show that \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} \Theta ^{2}}=a\sec ^{3}\Theta +b\sec \Theta \) giving the values of a and b.
(iii)Find the exact value of \(\int _{0}^{\frac{1}{4}\pi }(1+\tan ^{2}\Theta -3\sec \Theta \tan \Theta )d\Theta \).
Answer/Explanation
(i)Differentiate using chain or quotient rule
Obtain derivative in any correct form.
Obtain given answer correctly
(ii)Differentiate using product rule
State derivative of \(\tan \Theta =\sec ^{2}\Theta \)
Use trig identity \(1+\tan ^{2}\Theta =\sec ^{2}\Theta \) correctly
Obtain \(2\sec ^{3}\Theta -\sec \Theta \)
(iii)Use \(\tan ^{2}\Theta =\sec ^{2}\Theta -1\) to integrate \(\tan ^{2}\Theta \)
Obtain \(3\sec \Theta \) from integration of \(3\sec \Theta \tan \Theta \)
Obtain \(\tan \Theta -3\sec \Theta \)
Attempt to substitute limits ,using exact values
Obtain answer \(4-3\sqrt{2}\)
Question
The parametric equation of a curve are \(x=\ln (1-2t)\),\(y=\frac{2}{t}\) ,for \(t< 0\).
(i)Show that \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1-2t}{r^{2}}\).
(ii) Find the exact coordinates of the only point on the curve at which the gradient is 3.
Answer/Explanation
(i) State \(\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{-2}{1-2t}\) or \(\frac{\mathrm{d} y}{\mathrm{d} t}=-2t^{-2}\)
Use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} t}\div \frac{\mathrm{d} x}{\mathrm{d} t}\)
Obtain given answer correctly
(ii) Equate derivative to 3 and solve for t
State or imply that t = –1
Obtain coordinates (ln 3, –2)
Question
A curve has parametric equations \(x=\frac{1}{(2t+1)^{2}},y=\sqrt{(t+2)}\).
The point P on the curve has parameter p and it is given that the gradient of the curve at P is −1.
(i) Show that \(p=(p+2)^{\frac{1}{6}}-\frac{1}{2}\).
(ii) Use an iterative process based on the equation in part (i) to find the value of p correct to 3 decimalplaces. Use a starting value of 0.7 and show the result of each iteration to 5 decimal places
Answer/Explanation
(i) Obtain derivative of form\( k(2t+1)^{-3}\).
Obtain \(-4(2t+1)^{-3}\) or equivalent as derivative of x .
Obtain \(\frac{1}{2}(t+2)^{-\frac{1}{2}}\) or equivalent as derivative of y
Equate attempt at \(\frac{\mathrm{d} y}{\mathrm{d} x}\) to -1
Obtain \((2p+1)^{3}=8(p+2)^{\frac{1}{2}}\) or equivalent
Confirm given answer \( p=(p+2)^{\frac{1}{6}}-\frac{1}{2}\)
(ii) Use iteration process correctly at least once
Obtain final answer 0.678
Show sufficient iterations to 5 decimal places to justify answer or show a sign change in the interval (0.6775, 0.6785)
[0.7 → 0.68003 → 0.67857 → 0.67847 → 0.6784
Question
The diagram shows the curve\(y=4e^{\frac{1}{2}x}-6x+3\) and its minimum point M.
(i) Show that the x-coordinate of M can be written in the form ln a, where the value of a is to be stated.
(ii) Find the exact value of the area of the region enclosed by the curve and the lines x = 0, x = 2 and y = 0.
Answer/Explanation
(i) Differentiate to obtain expression of form \(ke^{\frac{1}{2}x}+m\)
Obtain correct \(2e^{\frac{1}{2}x}-6\)
Equate attempt at first derivative to zero and attempt solution
Obtain \( \frac{1}{2}x=\ln 3\) or equivalent
Conclude \(x=\ln 9\) or a=9
(ii) Integrate to obtain expression of form \(ae^{\frac{1}{2}x}+bx^{2}+cx\)
Obtain correct \(8e^{\frac{1}{2}x}-3x^{2}+3x\)
Substitute correct limits and attempt simplification
Obtain 8e – 14