Question
Use the trapezium rule with 3 intervals to estimate the value of \(\int_{0}^{3}|2^{x}-4|dx\)
Answer/Explanation
State or imply ordinates 3,2,0,4
Use correct formula,or equivalent,with h=1 and four ordinates
Obtain answer 5.5.
Question
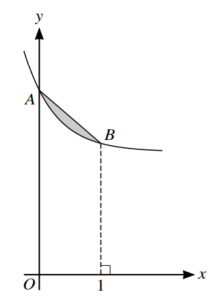
The diagram shows the curve y = 2 + e−2x
The curve crosses the y-axis at the point A, and the point B
on the curve has x-coordinate 1. The shaded region is bounded by the curve and the line segment AB.
Find the exact area of the shaded region. [5]
Answer/Explanation
Ans
3 State \(\frac{dx}{dt}-e^{t} + 2e^{-t}, \frac{dy}{dt}=6e^{2t}\)
\(\frac{dy}{dx}=\frac{dy}{dt}|\frac{dx}{dt}\) either in terms of t or after substitution of t = 0
Obtain gradient of tangent is 2 A1
Attempt equation of tangent with numerical gradient and coordinates
Obtain y = 2x + 6 or equivalent
Question
It is given that \(\int_{a}^{3a}\frac{2}{2x-5}dx=In\frac{7}{2}\).
Find the value of the positive constant a.
Answer/Explanation
Ans:
Integrate to obtain k In(2x-5)
Apply limits to obtain In(6a-5)-In(2a-5)=In\(\frac{7}{2}\)
Apply subtraction law for logarithms
Obtain equation\(\frac{6a-5}{2a-5}=\frac{7}{2}\)
Solve equation for a
Obtain \(a=\frac{25}{2}\)
Question
(a) Express \(5\sqrt{3}cos x + 5sin x\) in the form \(R cos(x- \alpha )\), where R>0 and \(0<\alpha<\frac{1}{2}\pi\).
(b) As x varies, find the least possible value of
\(4+5\sqrt{3}cos x+5sinx\),
and determine the corresponding value of x where \(-\pi<x<\pi\).
(c) Find \(\int \frac{1}{(5\sqrt{3}cos3\theta+5sin3\theta)^2}d\theta\)
Answer/Explanation
Ans:
- State R=10
Use appropriate trigonometry to find \(\alpha\)
Obtain \(\alpha=\frac{1}{6}\pi\) - State -6
Attempt to find x from their \(cos(x-\alpha)=-1\)
Obtain \(x-\frac{1}{6}\pi=-\pi\) and hence \(-\frac{5}{6}\pi\) - State integrand of form \(k_1sec^2(3\theta-\frac{1}{6}\pi)\)
Integrate to obtain form \(k_2tan(3\theta-\frac{1}{6}\pi)\)
Obtain \(\frac{1}{300}tan(3\theta-\frac{1}{6}\pi)+c\)
Question
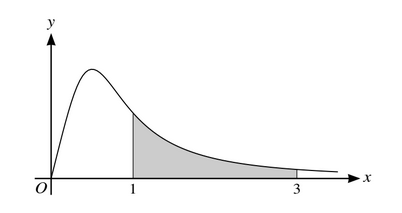
The diagram shows part of the curve with equation \(y=\frac{5x}{4x^3+1}\). The shaded region is bounded by the curve and the lines x=1, x=3 and y=0.
(a) Find \(\frac{dy}{dx}\) and hence find the the x-coordinate of the maximum point.
(b) Use the trapezium rule with two intervals to find an approximation to the area of the shaded region. Give your answer correct to 2 significant figures.
(c) State, with a reason, whether your answer to part (b) is an over-estimate or under-estimate of the exact area of the shaded region.
Answer/Explanation
Ans:
- Differentiate using quotient rule (or product rule)
Obtain \(\frac{5(4x^3+1)-60x^3}{(4x^3+1)^2}\)
Equate first derivative to zero and attempt solution
Obtain \(x=\frac{1}{2}\) - Use y values \(\frac{5}{5}, \frac{10}{33}, \frac{15}{109}\) or decimal equavalents
Use correct formula, or equivalent, with h=1
Obtain \(\frac{1}{2}(1+\frac{20}{30}+\frac{15}{109})\) or equivalent and hence 0.87 - State over-estimate with reference to top of each trapezium above curve
Question
A curve has equation \(y=f(x) \ where \ f(x)=\frac{4x^{3}+8x-4}{2x-1}\)
(a) Find an expression for\(\frac{dy}{dx}\) and hence find the coordinates of each of the stationary points of the
curve \(y=f(x)\) [5]
(b) Divide \(4x^{3}+8x-4 \ by \ (2x-1), \ and \ hence \ find \ \int f(x)dx\) [5]
Answer/Explanation
Ans
8(a) Differentiate using the quotient rule (or product rule)
Obtain \(\frac{(2x-1)(12x^{3}+8)-2(4x^{3}+8x-4)}{(2x-1)^{2}}\)
Equate first derivative to zero and attempt solution
Obtain (0, 4)
Obtain \(\left ( \frac{3}{4},\frac{59}{8} \right )\)
8 (b) Carry out division to obtain quotient of form 2x2 + kx + m
Obtain correct quotient \(2x^{2}+x+\frac{9}{2}\)
Obtain remainder \(\frac{1}{2}\)
Integrate to obtain at least \(k_{1}x^{3}\ and \ k_{2} \ ln(2x-1) \ terms\)
Obtain \(\frac{2}{3}x^{3}+\frac{1}{2}x^{2}+\frac{9}{2}x+\frac{1}{4}ln(2x-1)\) as final answer
Question
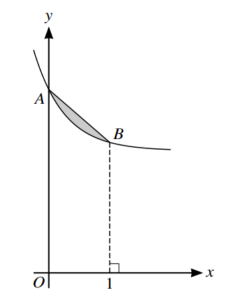
The diagram shows the curve y = 2 + e−2x. The curve crosses the y-axis at the point A, and the point B
on the curve has x-coordinate 1. The shaded region is bounded by the curve and the line segment AB.
Find the exact area of the shaded region. [5]
Answer/Explanation
Ans
3 Integrate to obtain form ax + be-2x
Obtain correct \(2x-\frac{1}{2}e^{-2x}\)
Apply limits to obtain \(\frac{5}{2}-\frac{1}{2}e^{-2}\)
Attempt to find area of relevant trapezium
Obtain \(\frac{5}{2}+\frac{1}{2}e^{-2}\) and subtract to obtain e−2 or exact equivalent
Question
(a) Use the trapezium rule with three intervals to find an approximation to \(\int_{1}^{4}\frac{6}{1+\sqrt{x}}dx\). Give your
answer correct to 5 significant figures. [3]
(b) Find the exact value of \(\int_{1}^{4}2e^{\frac{1}{2}x-2}dx\) [3]
(c) 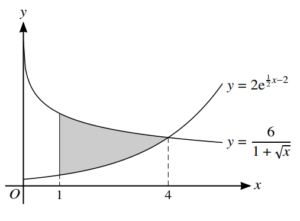
The diagram shows the curves \(y=\frac{6}{1+\sqrt{x}}\ and\ y=2e^{\frac{1}{2}x-2}\) which meet at a point with x-coordinate 4.
The shaded region is bounded by the two curves and the line x = 1.
Use your answers to parts (a) and (b) to find an approximation to the area of the shaded region.
Give your answer correct to 3 significant figures. [2]
(d) State, with a reason, whether your answer to part (c) is an over-estimate or under-estimate of the
exact area of the shaded region. [1]
Answer/Explanation
Ans
6 (a) Use y-values \(3, \frac{6}{1+\sqrt{2}},\frac{6}{1+\sqrt{3}}, 2\)
or \(3, 6\sqrt{2}-6, 3\sqrt{3}-3, 2\)
or 3, 2.4853…, 2.19615…, 2
Use correct formula, OE, with h=1
Obtain 7.1814
6 (b) Integrate to obtain form \(ke^{\frac{1}{2}x-2}\)
Obtain correct \(4e^{\frac{1}{2}x-2}\)
Obtain \(4-4e^{-\frac{3}{2}}\)
6 (c) Evaluate answer to part (a) minus answer to part (b)
Obtain 4.07
6 (d) State over-estimate with reference to top of each trapezium being
above the [first] curve, or clear equivalent, e.g. concave up so overestimate or convex down so over-estimate.
Question
(a)By first expanding cos (2θ + θ), show that cos 3θ = 4 cos3θ – 3 cos θ.
(b)Find the exact value of 2 cos3 \(\left ( \frac{5}{18}\pi \right ) – \frac{3}{2} cos \left ( \frac{5}{18} \pi \right )\) .
(c)Find \(\int (12cos^{3}x – 4 cos^{3} 3x)dx\) .
Answer/Explanation
(a)State cos 2θ cos θ – sin 2 θ sin θ
Attempt correct relevant identities to express in terms of cos θ only
Confirm 4 cos3 θ -3 cos θ with sufficient detail
(b)Use identity with θ = \(\frac{5}{18}\pi \)
Obtain \(\frac{1}{2} cos \frac{5}{6}\pi and hence – \frac{1}{4}\sqrt{3}\)
(c)Express integrand in form k1 (cos 3x + 3 cos x) + k2 (cos 9x + 3 cos 3x)
Obtain correct integrand 9 cos x – cos9 x
Integrate to obtain form k3 sin x + k4 sin 9x
Obtain correct 9 sin x – \(\frac{1}{9}\) sin 9x
Question
Find the exact value of \(\int_{-1}^{2} \left ( 4e^{2x} – 2e^{-x}\right )dx.\)
Answer/Explanation
Ans:
Integrate to obtain 2e2x
Integrate to obtain 2e−x
Apply limits correctly to integral of the form k1 e2x + k2e-x
Obtain 2e4 – 2e
Question
The polynomial p (x) is defined by
p(x) = 4x3 + 16x2 + 9x -15.
(a)Find the quotient when p(x) is divided by (2x+3), and show that the remainder is −6.
(b) Find \(\int \frac{p(x)}{2x+3}dx\) .
(c)Factorise p (x) +6 completely and hence solve the equation
p (cosec 2θ) + 6 = 0
for 00 < θ < 1350.
Answer/Explanation
Ans:
(a)Carry out division at least as far as 2x2 + kx
Obtain quotient 2x2 + 5x – 3
Confirm remainder is -6.
(b)Integrate to obtain at least k1 x 3 and k2 ln (2x 3) + terms
Obtain \(\frac{2}{3}x^{3} + \frac{5}{2}x^{2} – 3x – 3 In (2x+3)\)
(c)State or imply p(x) + 6 = (2x + 3) (2x2 + 5x -3)
Conclude (2x + 3) (2x – 1) (x + 3)
State or imply sin 2θ = \(-\frac{2}{3}\) or sin 2θ = \(-\frac{1}{3}\) or both
Carry out correct process to find θ in at least one case
Obtain 99.7 and 110.9
Question
(a)Given that y = \(tan^{2}x,\) show that \(\frac{dy}{dx} = 2 tan x + 2tan^{3}x.\)
(b)Find the exact value of \(\int_{\frac{1}{4}\pi }^{\frac{1}{3}\pi } \left ( tan x + tan^{2}x + tan^{3}x \right )dx\) .
Answer/Explanation
(a)Differentiate to obtain 2 tan x sec2 x
Use sec2 x = 1 + tan2 x to confirm 2 tan x + 2 tan3x
(b)Attempt to use part (a) result to integrate tan x + tan 3 x
Obtain \(\frac{1}{2}tan^{2}x\)
Use relevant identity to integrate tan2x
Obtain sec2 x−1 and hence tan x−x
Use limits correctly for integrand of form k1 tan2 x + k2 tan x + k3x
Obtain \(\sqrt{3} – \frac{1}{12}\pi \)
Question
(a)Show that sin 2θ cot θ − cos 2θ ≡ 1.
(bHence find the exact value of \(sin\frac{1}{6}\pi cot\frac{1}{12}\pi \).
(c) Find the smallest positive value of 1 (in radians) satisfying the equation
sin 2θ cotθ − 3 cos 2θ = 1.
Answer/Explanation
(a)Use at least two of sin 2θ = 2sin θ cos θ, cos 2θ = cos2θ – sin2θ, cotθ = \(\frac{cos\theta }{sin\theta }\)
Express LHS in terms of sin θ and cos θ only and attempt valid simplification
Obtain cos2 θ + sin2 θ or equivalent and hence 1
(b)Substitute θ = \(\frac{1}{12}\pi \) and show or imply \(sin\frac{1}{6}\pi cot\frac{1}{12}\pi = 1 + cos\frac{1}{6}\pi \)
Obtain 1+ \(\frac{1}{2}\sqrt{3}\) or exact equivalent
(c)Use the identity from part (a) to obtain − 2cos 2θ = 0 or equivalent
Obtain \(\theta = \frac{1}{4}\pi \)
Question
It is given that\( \int_{0}^{a}(3x^{2}+4cos2x-sinx)dx=2\)where a is a constant.
(i) Show that a=\(\sqrt[3]{(3-2sin2a-cosa)}\)
(ii) Using the equation in part (i), show by calculation that 0.5 < a < 0.75.
(iii) Use an iterative formula, based on the equation in part (i), to find the value of a correct to
3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
5(i) Integrate to obtain form \(x^{3}+k_{1}sin2x+k_{2}cosx\)
Obtain correct \(x^{3}+2sin2x+cosx\)
Apply limits correctly and equate to 2 Confirm given result
5(ii) Consider sign of \( a-\sqrt[3]{3-2sin2a-cosa}\) or equivalent for 0.5 and 0.75 Obtain –0.26 and 0.10 or equivalents and justify conclusion
5(iii) Use iterative process correctly at least once Obtain final answer 0.651 Show sufficient iterations to 5sf to justify answer or show a sign change in the interval [0.6505, 0.6515]
Question
Find the exact value of \(\int_{1}^{2}(2x^{2x-1})^{2}\) dx. Show all necessary working.
Answer/Explanation
Expand integrand to obtain \(4e^{4x}-4e^{2x}+1\) Integrate to obtain at least two terms of form \(k_{1}e^{4x}+k_{2}e^{2x}+k_{3}x\) Obtain correct \(e^{4x}-2e^{2x}+x \)
Apply both limits correctly to their integral obtain \(e^{8}-3e^{4}+2e^{2}+1\)
Question
(a) Find \(\int tan^{2}3xdx\)
(b) Find the exact value of \(\int_{0}^{1}\frac{e^{3x}+4}{e^{x}}\)dx Show all necessary working.
Answer/Explanation
<p(a) Use identity \(\tan ^{2}3x=\sec ^{2}3x-1\)
Integrate to obtain from \(k_{1}\tan 3x+k_{2}x\).
Obtain correct \(\frac{1}{3}\cos 3x-x+c\)
(b)
Express integrand as \(e^{2x}+4e^{-x}\).
Integrate to obtain from \( k_{3}e^{2x}+k_{4}e^{-x}\)
Obtain correct \(\frac{1}{2}e^{2x}-4e^{-x}\)
Use limits top obtain \(\frac{1}{2}e^{2}-4e^{-1}+\frac{7}{2}\) or similarly simplified equivalent
Question
The diagram shows the curve with equation\( y =\sqrt{(1+3cos^{2}(\frac{1}{2}))}\)for 0 ≤ x ≤ 0. The region R is bounded by the curve, the axes and the line x =\( \pi\) .
(i) Use the trapezium rule with two intervals to find an approximation to the area of R, giving your answer correct to 3 significant figures.
(ii) The region R is rotated completely about the x-axis. Without using a calculator, find the exact volume of the solid produced.
Answer/Explanation
6(i) Use y values 2 \(\sqrt{2.5}\) , 1 or equivalents
Use correct formula, or equivalent, with\( h=\frac{1}{2}\pi \) and three y values
Obtain\( \frac{1}{2}\times \frac{1}{2}\pi (2+\sqrt[2]{2.5}+1)\) or equivalent and hence 4.84
6(ii) State or imply volume is \(\int \pi (1+3cos^{2}\frac{1}{2}x)dx\)
Use appropriate identity to express integrand in form \(k_{1}+k_{2}cosx\)
Obtain \(\int \pi (\frac{5}{2}+\frac{3}{2}cosx)dx or \int (\frac{5}{2}x+\frac{3}{2}cosx)dx\)
Integrate to obtain\( \pi (\frac{5}{2}x+\frac{3}{2}sinx) or \frac{5}{2}x+\frac{3}{2}x\)
Obtain\( \frac{5}{2}\pi ^{2}\) with no errors seen
Question
Show that\(\int_{1}^{7}\frac{6}{2x+1}dx\)= In 125
Integrate to obtain form k ln(2x+1)
Answer/Explanation
Obtain correct 3 ln(2x+1)
Use subtraction law of logarithms correctly
Use power law of logarithms correctly
Confirm ln 125
Question
It is given that \(\int_{0}^{a}(3x^{2}+4cos2x-sinx)dx=2,\)
where a is a constant.
(i) Show that a =\(\sqrt[3]{(3-2sin2a-cosa)}\).
(ii) Using the equation in part (i), show by calculation that 0.5 < a < 0.75.
(iii) Use an iterative formula, based on the equation in part (i), to find the value of a correct to
3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
(i)obtain \(\frac{\mathrm{d} x}{\mathrm{d} \Theta }= -4sin2\Theta +3cos\Theta \)
use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\frac{\mathrm{d} y}{\mathrm{d} y\Theta }}{\frac{\mathrm{d}x }{\mathrm{d} \Theta }}\) in terms of \(\Theta \) or which 1 already substituted.
obtain or imply \(\frac{dy}{dx}=\frac{-3sin\Theta }{-4sin2\Theta +3cos\Theta }\)
substitute 1 to get \(1.25\)
(ii) Equate denominator of first derivative to zero
use \(sin2\Theta=2sin\Theta cos\Theta\)
obtain \(sin\Theta=\frac{3}{8}\)
Question
It is given that \(\int_{0}^{a}(3x^{2}+4cos2x-sinx)dx=2,\)
where a is a constant.
(i) Show that a =\(\sqrt[3]{(3-2sin2a-cosa)}\).
(ii) Using the equation in part (i), show by calculation that 0.5 < a < 0.75.
(iii) Use an iterative formula, based on the equation in part (i), to find the value of a correct to
3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
(i)obtain \(\frac{\mathrm{d} x}{\mathrm{d} \Theta }= -4sin2\Theta +3cos\Theta \)
use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\frac{\mathrm{d} y}{\mathrm{d} y\Theta }}{\frac{\mathrm{d}x }{\mathrm{d} \Theta }}\) in terms of \(\Theta \) or which 1 already substituted.
obtain or imply \(\frac{dy}{dx}=\frac{-3sin\Theta }{-4sin2\Theta +3cos\Theta }\)
substitute 1 to get \(1.25\)
(ii) Equate denominator of first derivative to zero
use \(sin2\Theta=2sin\Theta cos\Theta\)
obtain \(sin\Theta=\frac{3}{8}\)
Question
It is given that \(\int_{0}^{a}(3x^{2}+4cos2x-sinx)dx=2,\)
where a is a constant.
(i) Show that a =\(\sqrt[3]{(3-2sin2a-cosa)}\).
(ii) Using the equation in part (i), show by calculation that 0.5 < a < 0.75.
(iii) Use an iterative formula, based on the equation in part (i), to find the value of a correct to
3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
(i)obtain \(\frac{\mathrm{d} x}{\mathrm{d} \Theta }= -4sin2\Theta +3cos\Theta \)
use \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\frac{\mathrm{d} y}{\mathrm{d} y\Theta }}{\frac{\mathrm{d}x }{\mathrm{d} \Theta }}\) in terms of \(\Theta \) or which 1 already substituted.
obtain or imply \(\frac{dy}{dx}=\frac{-3sin\Theta }{-4sin2\Theta +3cos\Theta }\)
substitute 1 to get \(1.25\)
(ii) Equate denominator of first derivative to zero
use \(sin2\Theta=2sin\Theta cos\Theta\)
obtain \(sin\Theta=\frac{3}{8}\)
Question
A curve has equation y = \(y=\frac{3+2 Inx}{1+Inx}.\) Find the exact gradient of the curve at the point for which \(y = 4\).
Answer/Explanation
Rewrite integrand as \(4e^{2x}+4e^{-x}\) Integrate to obtain form \(k_{1}e^{2x}+k_{2}e^{-x}\) where\( k_{1}\neq 4,k_{2}\neq 4\)
Obtain correct \(2e^{2x}-4e^{-x}\)
Apply limits correctly, retaining exactness
Obtain \(2e^{4}-4e^{-2}+2\) or exact similarly simplified equivalent
Question
Find the exact value of \(\int_{1}^{2}(2e^{2x}-1)^{2}dx.\)Show all necessary working.
Answer/Explanation
Either
State or imply equation y= A ln B ln x
Equate gradient of line to ln B
Obtain ln 1.6486… B= and hence B= 5.2
Substitute appropriate values to find ln A
Obtain ln 1.2809… A= and hence A = 3.6
Or
State or imply equation ln A+In B In x
Use given coordinates to obtain a correct equation
Use given coordinates to obtain a second correct equation and attempt to
solve both equations simultaneously to obtain at least one of the unknowns ln
A or lnB
Obtain ln 1.6486… B= and hence B = 5.2
Obtain ln 1.2809… A = and hence A = 3.6
Or
Use given coordinates to obtain a correct equation
Use given coordinates to obtain a second correct equation
Solve to obtain B
B= 5.2
A = 3.6
Question
(a) Show that \(\int_{1}^{4}\left ( \frac{2}{x} +\frac{2}{2x+1}\right ) \) dx = ln 48.
(b) Find\( \int sin2x(cotx+2cosecx)dx\)
Answer/Explanation
6(a) Integrate to obtain form \(k_{1}In x+k_{2}In (2x+1)\)
Obtain correct 2ln x+In(2x+1)
Use logarithm addition/subtraction property correctly
Use logarithm power property correctly Confirm ln 48 with no errors seen
6(b) Use identity sin2x = 2sin xcos x
State or imply
Attempt to express integrand in terms of cos 2x and cosx
Obtain correct integrand 1+ cos 2x +4cosx
Integrate to obtain at least terms\( k_{3}sin2x and k_{4}sinx\)
Obtain correct \(x+\frac{1}{2}sin2x+4sinx+c\)
Question
(a) Find \(\int \frac{1+Cos^{4}2x}{cos^{2}2x}\)
(b) Without using a calculator, find the exact value of dx, giving your answer in the form ln , where a and b are integers
Answer/Explanation
.
Question
(i) Show that sin 2x cot x Ξ 2 cos2x. [2]
(ii) Using the identity in part (i),
(a) find the least possible value of
3 sin 2x cot x + 5 cos 2x + 8
as x varies, [4]
(b) find the exact value of \(\int_{\frac{1}{8}\pi }^{\frac{1}{6}\pi}\) cosec 4x tan 2x dx. [5]
Answer/Explanation
Ans:
8 (i) State cos 2sin x cos x . \(\frac{cos x}{sin x}\)
Simplify to confirm 2cos2x
(ii) (a) Use cos2x= 2cos2 x-1
Express in terms of cos x
Obtain 16cos2 x + 3 or equivalent
State 3, following their expression of form a cos2 x + b
(b) Obtain integrand as \(\frac{1}{2}sec^{2}2x\)
Integrate to obtain form k tan 2x
Obtain correct \(\frac{1}{2}tan2x\)
Apply limits correctly dep
Obtain \(\frac{1}{4}\sqrt{3}-\frac{1}{4}\) or exact equivalent
Question
Given that \(\int_{0}^{a}6e^{2x+1}dx=65\) , find the value of a correct to 3 decimal places.[5]
Answer/Explanation
Ans:
5 Obtain integral of form ke2x+1
Obtain correct 3e2x+1
Apply both limits correctly and rearrange at least to e2a+1 = …
Use logarithms correctly to find a
Obtain 1.097
Question
(a) Find \(\int \left ( tan^{2}x +sin2x\right )dx.\) [3]
(b) Find the exact value of \(\int_{0}^{1}3e^{1-2x}dx.\) [4]
Answer/Explanation
Ans:
5 (a) Use tan2 x = sec2 x – 1
Obtain integral of form p tan x + qx + r cos 2x
Obtain x − x − \(\frac{1}{2}\) cos 2x + c
(b) Obtain integral of form ke1-2x
Obtain \(-\frac{1}{2}e^{1-2x}\)
Apply both limits the correct way round
Obtain \(-\frac{1}{2}e^{-1}+\frac{1}{2}e\) or exact equivalent
Question
(i) Given that \(\int_{0}^{a}\left ( 3e^{\frac{1}{2}x}+1 \right )dx=10\), show that the positive constant a satisfies the equation [5]
\(a = 2ln\left ( \frac{16-a}{6} \right )\)
(ii) Use the iterative formula \(a_{n+1} = 2ln\left ( \frac{16-a_{n}}{6} \right )\) with a1 = 2 to find the value of a correct to 3 decimal places. Give the result of each iteration to 5 decimal places. [3]
Answer/Explanation
Ans:
5 (i) Obtain integral of form \(ke^{\frac{1}{2}x}+ mx\)
Obtain correct \(6e^{\frac{1}{2}x}+ x\)
Apply limits and obtain correct \(6e^{\frac{1}{2}a}+a-6\)
Equate to 10 and introduce natural logarithm correctly DM1
Obtain given answer \(a=2ln\left ( \frac{16-a}{6} \right )\) correctly
(ii) Use the iterative formula correctly at least once
Obtain final answer 1.732
Show sufficient iterations to justify accuracy to 3 d.p. or show sign change in interval (1.7315, 1.7325)
Question
(a) Find
(i)\(\int \frac{e^{2x}+6}{e^{2x}}\),
(ii) \(\int 3\cos ^{2}xdx\),
(b) Use the trapezium rule with 2 intervals to estimate the value of,
\(\int _{1}^{2}\frac{6}{\ln (x+2)}dx\),
giving your answer correct to 2 decimal places.
Answer/Explanation
(a) (i) Attempt to divide by \(e^{2x}\) and attempt to integrate 2 terms
Integrate a term of form \(ke^{-2x}\) correctly.
Fully correct integral \(x-3e^{-2x}\).
(ii) State correct expression \(\frac{1}{2}\cos 2x+\frac{1}{2}\) or equivalent
Integrate an expression of the form a + b cos 2x, where ab ≠ 0, correctly
State correct integral \(\frac{3\sin 2x}{4}+\frac{3x}{2}\).
(b) State or imply correct ordinates 5.46143…, 4.78941…, 4.32808…
Use correct formula, or equivalent, correctly with h = 0.5 and three ordinates
Obtain answer 4.84 with no errors seen
Question
(i) Show that \(12\sin ^{2}x\cos ^{2}x=\frac{3}{2}(1-\cos 4x)\)
(ii) Hence show that
\(\int _{\frac{1}{4}\pi }^{\frac{1}{3}\pi }12\sin ^{2}x\cos ^{2}xdx=\frac{\pi }{8}+\frac{3\sqrt{3}}{16}\).
Answer/Explanation
(i) Either
Use \(\sin 2x=2\sin x\cos x\) to convert integrand to \(k\sin ^{2}2x\)
Use \(\cos 4x=1-2\sin ^{2}2x\)
State correct expression \(\frac{1}{2}-\frac{1}{2}\cos 4x\) or equivalent.
Or
Use \(\cos ^{2}x=\frac{1-\cos 2x}{2}\) and/or \(x=\frac{1-\cos 2x}{2}\) to obtain an equation in cos 2x only
Use \(\cos ^{2}2x=\frac{1+\cos 4x}{2}\).
State correct expression \(\frac{1}{2}-\frac{1}{2}\cos 4x\) or equivalent.
(ii) State correct integral \(\frac{3}{2}x-\frac{3}{8}\sin 4x\)
Attempt to substitute limits, using exact values
Obtain given answer correctly
Question
(i) By differentiating \(\frac{1}{\cos \Theta }\), show that if \(y=\sec \Theta \) then \(\frac{\mathrm{d} y}{\mathrm{d} \Theta }=\tan \Theta \sec \Theta \).
(ii)Hence show that \(\frac{\mathrm{d} ^{2}y}{\mathrm{d} \Theta ^{2}}=a\sec ^{3}\Theta +b\sec \Theta \) giving the values of a and b.
(iii)Find the exact value of \(\int _{0}^{\frac{1}{4}\pi }(1+\tan ^{2}\Theta -3\sec \Theta \tan \Theta )d\Theta \).
Answer/Explanation
(i)Differentiate using chain or quotient rule
Obtain derivative in any correct form.
Obtain given answer correctly
(ii)Differentiate using product rule
State derivative of \(\tan \Theta =\sec ^{2}\Theta \)
Use trig identity \(1+\tan ^{2}\Theta =\sec ^{2}\Theta \) correctly
Obtain \(2\sec ^{3}\Theta -\sec \Theta \)
(iii)Use \(\tan ^{2}\Theta =\sec ^{2}\Theta -1\) to integrate \(\tan ^{2}\Theta \)
Obtain \(3\sec \Theta \) from integration of \(3\sec \Theta \tan \Theta \)
Obtain \(\tan \Theta -3\sec \Theta \)
Attempt to substitute limits ,using exact values
Obtain answer \(4-3\sqrt{2}\)
Question
(a) Use the trapezium rule with two intervals to estimate the value of
\(\int _{0}^{1}\frac{1}{6+2e^{x}}dx\)
giving your answer correct to 2 decimal places.
(b) Find \(\int \frac{(e^{x}-2)^{2}}{e^{2x}}dx.\)
Answer/Explanation
(a) State or imply correct ordinates 0.125, 0.08743…, 0.21511… B1
Use correct formula, or equivalent, correctly with h = 0.5 and three ordinates M1
Obtain answer 0.11 with no errors seen
(b) Attempt to expand brackets and divide by \(e^{2x}\)
Integrate a term of form \(ke^{-x}\) or \(ke^{-2x}\) correctly
Obtain 2 correct terms
Fully correct integral \(x+4e^{-x}-2e^{-2x}+c\)
Question
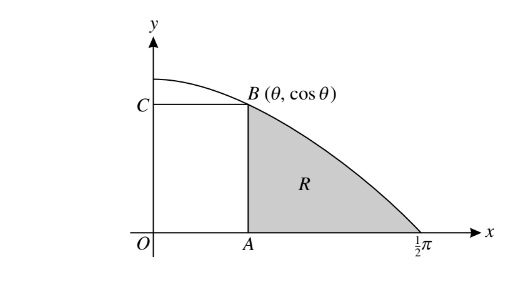
The diagram shows the curve y = cos x, for 0 ≤ x ≤π. A rectangle OABC is drawn, where B is the point on the curve with x-coordinate θ, and A and C are on the axes, as shown. The shaded region R is bounded by the curve and by the lines x = θ and y = 0.
(i) Find the area of R in terms of θ.
(ii) The area of the rectangle OABC is equal to the area of R. Show that \(\Theta =\frac{1-\sin \Theta }{\cos \Theta }\)
(iii) Use the iterative formula \(\Theta _{n+1}=\frac{1-\sin \Theta }{\cos \Theta }\), with initial value θ1= 0.5, to determine the value of θ correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i)Attempt to integrate and use limits θ and π
Obtain 1– sin θ
(ii) State that area of rectangle = θcos θ, equate area of rectangle to area of R
and rearrange to given equation
(iii) Use the iterative formula correctly at least once
Obtain final answer 0.56
Show sufficient iterations to justify its accuracy to 2 d.p. or show there is a
sign change in the interval (0.555, 0.565)
Question
(i) Show that \((2\sin x+\cos x)^{2}\) can be written in the form \(\frac{5}{2}+2\sin 2x-\frac{3}{2}\cos 2x\).
(ii) Hence find the exact value of \(\int ^{\frac{1}{2}\pi }_{0}(2\sin x+\cos x)^{2}dx.\)
Answer/Explanation
(i)Expand to obtain \(4\sin ^{2}x+4\sin x\cos x+\cos ^{2}x\).
Use \(2\sin x\cos x=\sin 2x\).
Attempt to express \(\sin ^{2}x\) or \(\cos ^{2}x\)(or both) in terms of \(\cos 2x\)
Obtain correct \(\frac{1}{2}k(1-\cos 2x)\) for their or equivalent \(k\sin ^{2}x\) or equivalent
\(\frac{5}{2}+2\sin 2x-\frac{3}{2}\cos 2x\).
(ii)Integrate to obtain form \(px+q\cos 2x+r\sin 2x\)
Obtain \(\frac{5}{2}x-\cos 2x-\frac{3}{4} \sin 2x.\)
Substitute limits in integral of form \(px+q\cos 2x+r\sin 2x\) and attempt simplification
Obtain \(\frac{5}{8}\pi +\frac{1}{4}\) or exact equivalent
