Question
A curve has equation \(y=x^3e^{0.2x}\) where \(x\geq0\). At the point P on the curve, the gradient of the curve is 15.
(a) Show that the x-coordinates of P satisfies the equation \(x=\sqrt{75e^{0.2x}}{15+x}\).
(b) Use the equation in part (a) to show by calculation that the x-coordinate of P lies between 1.7 and 1.8
(c) Use an iterative formula, based on the equation in part (a), to find the x-coordinate of P correct to 4 significant figures. Gives the result of each iteration to 6 significant figures.
Answer/Explanation
Ans:
(a) Differentiate using the product rule
(b) Obtain \(3x^2e^{0.2x}+0.2x^3e^{0.2x}\)
Equate first derivative to 15 and rearrange to x = …..
Confirm \(x=\sqrt{\frac{75e^{-0.2x}}{15+x}}\)
(b) Consider sign of \(x-\sqrt{\frac{75e^{-0.2x}}{15+x}}\) or equivalent for 1.7 and 1.8
Obtain -0.08…. and 0.03….. or equivalent for 1.7 and 1.8
Obtain -0.08… and 0.03… or equivalents and justify conclusion
(c) Use iterative process correctly at least once
Obtain final answer 1.771
Show sufficient iterations to 6 sf to justify answer or show a sign change in the interval [1.7705, 1.7715]
Question
(a) Given that 2 In(x+1) + In x = In(x+9), show that \(x=\sqrt{\frac{9}{x+2}}\).
(b) It is given that the equation \(x=\sqrt{\frac{9}{x+2}}\) has single root
Show by calculation that this root lies between 1.5 and 2.0
(c) Use an iterative formula, based on the equation in part (b), to find the root correct to 3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
Ans:
- Use the power law correctly
Use correct process to obtain equation with no logarithms
Confirm \(x=\sqrt{\frac{9}{x+2}}\) - Consider sign of \(x-\sqrt{\frac{9}{x+2}}\)
Obtain -0.1…. and 0.5 or equivalents and justify conclusion - Use iteration process correctly at least once
Obtain final answer 1.58
Show sufficient iterations to 5 sf to justify answer or show a sign change in interval [1.575, 1.585]
Question
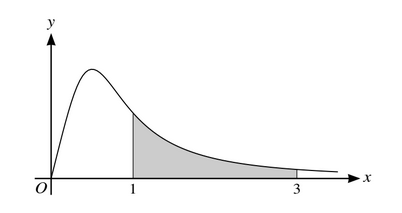
The diagram shows part of the curve with equation \(y=\frac{5x}{4x^3+1}\). The shaded region is bounded by the curve and the lines x=1, x=3 and y=0.
(a) Find \(\frac{dy}{dx}\) and hence find the the x-coordinate of the maximum point.
(b) Use the trapezium rule with two intervals to find an approximation to the area of the shaded region. Give your answer correct to 2 significant figures.
(c) State, with a reason, whether your answer to part (b) is an over-estimate or under-estimate of the exact area of the shaded region.
Answer/Explanation
Ans:
- Differentiate using quotient rule (or product rule)
Obtain \(\frac{5(4x^3+1)-60x^3}{(4x^3+1)^2}\)
Equate first derivative to zero and attempt solution
Obtain \(x=\frac{1}{2}\) - Use y values \(\frac{5}{5}, \frac{10}{33}, \frac{15}{109}\) or decimal equavalents
Use correct formula, or equivalent, with h=1
Obtain \(\frac{1}{2}(1+\frac{20}{30}+\frac{15}{109})\) or equivalent and hence 0.87 - State over-estimate with reference to top of each trapezium above curve
Question
The sequence of values given by the iterative formula \(x_{n+1}=\frac{6+8x_{n}}{8+x^{2}_{n}}\) with initial value x1 = 2 converges
to \(\alpha \)
(a) Use the iterative formula to find the value of ! correct to 4 significant figures. Give the result of
each iteration to 6 significant figures. [3]
(b) State an equation satisfied by \(\alpha \) and hence determine the exact value of \(\alpha \) [2]
Answer/Explanation
Ans
(a) Use iteration correctly at least once
Obtain final answer 1.817 A1 Answer required to exactly 4 significant figures
Show sufficient iterations to 6 significant figures to justify answer
or show sign change in interval [1.8165, 1.8175]
(b) State equation \(x=\frac{6+8X}{8+x^{2}}\ or \ equivalent \ using \ \alpha \)
Obtain \(\sqrt[3]{6}\) or exact equivalent
Question
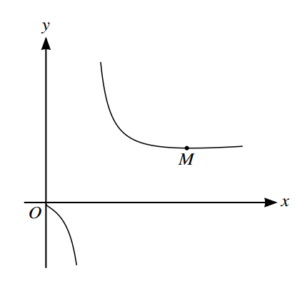
The diagram shows the curve with equation \(y=\frac{3x+2}{ln x} \). The curve has a minimum point M.
(a) Find an expression for \(\frac{dy}{dx}\) and show that the x-coordinate of M satisfies the equation \(x=\frac{3x+2}{3 lnx}\)
(b) Use the equation in part (a) to show by calculation that the x-coordinate of M lies between
3 and 4. [2]
(c) Use an iterative formula, based on the equation in part (a), to find the x-coordinate of M correct
to 5 significant figures. Give the result of each iteration to 7 significant figures. [3]
Answer/Explanation
Ans
5 (a) Use quotient rule (or equivalent) to find first derivative
Obtain \(\frac{dy}{dx}=\frac{3ln x-\frac{1}{x}(3x+2)}{(lnx)^{2}}\)
Equate first derivative to zero and confirm \(x=\frac{3x+2}{3lnx}\)
5 (b) Consider \(x-\frac{3x+2}{3lnx}\) or equivalent for values 3 and 4
Obtain −0.33… and 0.63… or equivalents and justify conclusion
5 (c) Use iteration process correctly at least once
Obtain final answer 3.3223
Show sufficient iterations to 7 s.f. to justify answer or show sign
change in the interval [3.32225, 3.32235]
Question
The curve with equation y = xe2x + 5e−x has a minimum point M.
(a)Show that the x-coordinate of M satisfies the equation x = \(\frac{1}{3}\) ln 5 − \(\frac{1}{3}\) ln (1 + 2x).
(b)Use an iterative formula, based on the equation in part (a), to find the x-coordinate of M correct to 3 significant figures. Use an initial value of 0.35 and give the result of each iteration to 5 significant figures.
Answer/Explanation
(a)Attempt use of product rule to differentiate xe2x
Obtain e2x + 2xe2x – 5e-x
Equate first derivative to zero and multiply by ex to obtain an equation involving e3x
Obtain e3x(1 + 2x) = 5 or equivalent
Confirm given result x = \(\frac{1}{3}\) ln5 – \(\frac{1}{3}\) ln (1 + 2x) with sufficient detail.
(b)Use iteration process correctly at least once
Obtain final answer 0.357
Show sufficient iterations to 5sf to justify answer or show sign change in interval [0.3565, 0.3575]
Question
A curve has equation e2xy – ey = 100.
(a)Show that \(\frac{dy}{dx}=\frac{2e^{2x}y}{e^{y-e^{2x}}}.\)
(b)Show that the curve has no stationary points.
It is required to find the x-coordinate of P, the point on the curve at which the tangent is parallel to the y-axis.
(c)Show that the x-coordinate of P satisfies the equation.
x = ln 10 \(-\frac{1}{2}In (2x-1)\)State or imply ey – e2x = 0 and hence y = 2x
(d)Use an iterative formula, based on the equation in part (c), to find the x-coordinate of P correct to 3 significant figures. Use an initial value of 2 and give the result of each iteration to 5 significant figures.
Answer/Explanation
(a)Use product rule to differentiate e2x y
Obtain \(2e^{2x}y+e^{2x}\frac{dy}{dx}\)
Obtain \(2e^{2x}y+e^{2x}\frac{dy}{dx}- e^{y}\frac{dy}{dx} = 0\) and rearrange to confirm given result.
(b)Consider e2xy = 0 and either state e2x ≠ 0 or substitute y = 0 in equation of curve
Complete argument with e2x ≠ 0 or e2x> 0 and substitution to show y cannot be zero.
(c)Substitute for y in equation of curve and attempt rearrangement as far as e2x = …..
Use relevant logarithm properties
Confirm equation \(x = In 10 – \frac{1}{2}In (2x-1)\)
(d)Use iteration process correctly at least once
Obtain final answer 1.82
Show sufficient iterations to 5 sf to justify answer or show sign change in interval [1.815, 1.825]
Question
It is given that\( \int_{0}^{a}(3x^{2}+4cos2x-sinx)dx=2\)where a is a constant.
(i) Show that a=\(\sqrt[3]{(3-2sin2a-cosa)}\)
(ii) Using the equation in part (i), show by calculation that 0.5 < a < 0.75.
(iii) Use an iterative formula, based on the equation in part (i), to find the value of a correct to
3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
5(i) Integrate to obtain form \(x^{3}+k_{1}sin2x+k_{2}cosx\)
Obtain correct \(x^{3}+2sin2x+cosx\)
Apply limits correctly and equate to 2 Confirm given result
5(ii) Consider sign of \( a-\sqrt[3]{3-2sin2a-cosa}\) or equivalent for 0.5 and 0.75 Obtain –0.26 and 0.10 or equivalents and justify conclusion
5(iii) Use iterative process correctly at least once Obtain final answer 0.651 Show sufficient iterations to 5sf to justify answer or show a sign change in the interval [0.6505, 0.6515]
Question
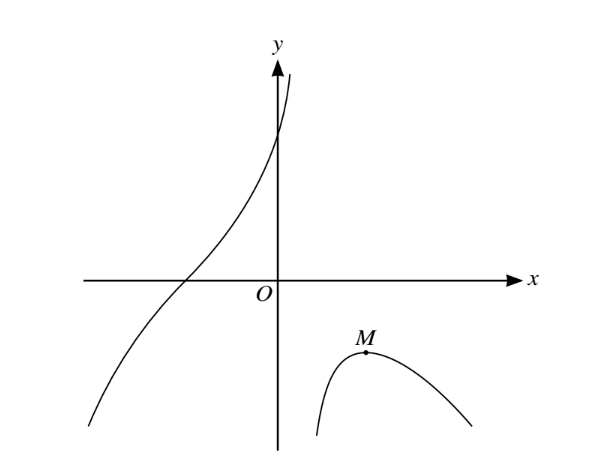
The diagram shows the curve with equation y=\(\frac{8+x^{3}}{2-5x}\).The maximum point is denoted by M.
(i) Find an expression for \(\frac{dy}{dx}\) and determine the gradient of the curve at the point where the curve crosses the x-axis.
(ii) Show that the x-coordinate of the point M satisfies the equation x =\(\sqrt{(0.6x+4x^{-1})}.\)
(iii) Use an iterative formula, based on the equation in part (ii), to find the x-coordinate of M correct to 3 significant figures. Give the result of each iteration to 5 significant figures.
Answer/Explanation
<p(i) Use quotient rule (or product rule) to differentiate .
Obtain \(\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{3x^{2}\left ( 2-5x \right )-\left ( -5 \right )\left ( 8+x^{3} \right )}{\left ( 2-5x \right )^{2}}\)
State or imply curve crosses x-axiz when x=-2.
Substitute -2 to obtain 1
(ii)Equate numerator of first derivative to zero and rearrange as far as \(kx^{3}\)=….or equivalent
Confirm given result \(x=\sqrt{0.6x+4x^{-1}}\)
(iii) Use iterative process correctly atleast once
Obtain final answer 1.81
Show sufficient iterations to 5sf to justify answer or show a sign change in the interval \(\left [ 1.805,1.815 \right ]\)
Question
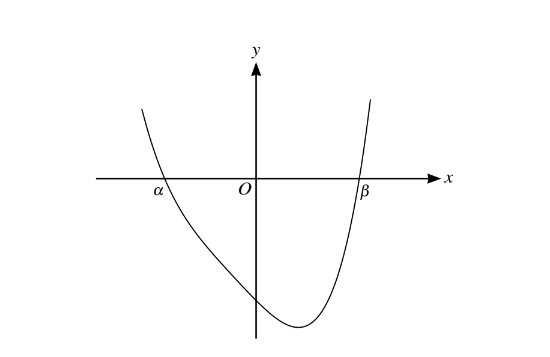
The diagram shows the curve with equation
\(y=x^{4}+2x^{3}+2x^{2}-12x-32\)
The curve crosses the x-axis at points with coordinates (\alpha ,0)(\beta ,0).
(i) Use the factor theorem to show that (x + 2 )is a factor of \(y=x^{4}+2x^{3}+2x^{2}-12x-32\)
(ii) Show that \(\beta\) satisfies an equation of the form x=\(\sqrt[3]{(p+qx)}\)and state the values of p and q.
(iii) Use an iterative formula based on the equation in part (ii) to find the value of\( \beta\)correct to4 significant figures. Give the result of each iteration to 6 significant figures.
Answer/Explanation
4(i) Substitute –2 and simplify
Obtain 16 -16 8 +24 -32 −and hence zero and conclude
4(ii) Attempt division by
x+2 to reach at least partial quotient\( x^{3}+kx\)or use of identity or inspection
Obtain\( x^{3}+2x-16\) Equate to zero and obtain x=\(\sqrt[3]{16-2x}\)
4(iii) Use iteration process correctly at least once
Obtain final answer 2.256
Show sufficient iterations to 6 sf to justify answer or show a sign change in the interval (2.2555, 2.2565)
Question
The equation of a curve is \(y=\frac{e^{2x}}{4x+1}\) and the point P on the curve has y-coordinate 10.
(i) Show that the x coordinate of P satisfies the equation\( x=\frac{1}{2}In(40x+10).\)
(ii) Use the iterative formula \(x_{n+1}=\frac{1}{2}In(40x_{n}+10)with x_{1}= 2.3\) to find the x-coordinate of P correct
to 4 significant figures. Give the result of each iteration to 6 significant figures.
(iii) Find the gradient of the curve at P, giving the answer correct to 3 significant figures.
Answer/Explanation
5(i) Attempt rearrangement of\( \frac{e^{2x}}{4x+1}=10 to x=….. \)involving ln
Confirm\( x=\frac{1}{2} In(40x+10)\)
5(ii) Use iteration process correctly at least once Obtain final answer 2.316 A1
Show sufficient iterations to 6 sf to justify answer or show a sign change in the interval [2.3155, 2.3165]
5(iii) Use quotient rule (or product rule) to find derivative Obtain \(\frac{2e^{2x}(4x+1)-4e^{2x}}{(4x+1)^{2}} \)or equivalent Substitute answer from part (ii) (or more accurate value) into attempt at first derivative Obtain 16.1
Question
It is given that a is a positive constant such that
\( \int _{0}^{a}(1+2x+3e^{3x})dx=250.\)
(i) Show that\( a-\frac{1}{3}In (251-a-a^{2})\)
(ii) Use an iterative formula based on the equation in part (i) to find the value of a correct to 4 significant figures. Give the result of each iteration to 6 significant figures.
Answer/Explanation
Integrate to obtain form \(k_{1}x+k_{2}x^{2}+k_{3}e^{3x}\) for non-zero constants
Obtain\( x+x^{2}+e^{3x}\)
Apply both limits to obtain \(a+a^{2}+e^{3a}-1\)=250 or equivalent
Apply correct process to reach form without e involved
Confirm given\( a=\frac{1}{3}In (251-a-a^{2})\)
(ii) Use iterative process correctly at least once
Obtain final answer 1.835
Show sufficient iterations to 6 sf to justify answer or show
sign change in interval (1.8345, 1.8355)
Question
The equation of a curve is y =\( \frac{3x^{2}}{x^{2}+4}\) At the point on the curve with positive x-coordinate p, the gradient of the curve is -\(\frac{1}{2}\)
(i) Show that p =\( \sqrt{\left ( \frac{48p-16}{p^{2}+8} \right )}\)
(ii) Show by calculation that 2 < p < 3.
(iii) Use an iterative formula based on the equation in part (i) to find the value of p correct to 4 significant figures. Give the result of each iteration to 6 significant figures
Answer/Explanation
.
(i) Use quotient rule or equivalent
Obtain or equivalent
Equate first derivative to and remove algebraic denominators dep on
Obtain or equivalent
Confirm given result
(ii) Consider sign of at 2 and 3 or equivalent
Complete argument correctly with appropriate calculations
(iii) Carry out iteration process correctly at least once Obtain final answer 2.728 Show sufficient iterations to justify accuracy to 4 sf or show sign change
in interval (2.7275, 2.7285)
Question
The sequence of values given by the iterative formula
\(x_{n+1}=\sqrt{\frac{1}{2}x_{n}^{2}+4x_{n}^{-3}}\) ,
with initial value x1= 1.5, converges to α.
(i) Use this iterative formula to find α correct to 3 decimal places. Give the result of each iteration to 5 decimal places.[3]
(ii) State an equation that is satisfied by α and hence find the exact value of α.[2]
Answer/Explanation
Ans:
4 (i) Use the iterative formula correctly at least once
Obtain final answer 1.516
Show sufficient iterations to justify accuracy to 3 dp or show sign change in interval (1.5155,1.5165)
(ii) State equation \(x=\sqrt{\frac{1}{2}x^{2}+4x^{-3}}\) or equivalent
Obtain exact value \(\sqrt[5]{8}\) or \(8^{0.2}\)
Question
(i) By sketching a suitable pair of graphs, show that the equation
ln x = 4 − \(\frac{1}{2}x\)
has exactly one real root, α. [2]
(ii) Verify by calculation that 4.5 < α < 5.0. [2]
(iii) Use the iterative formula xn+1= 8 − 2 ln xn to find α correct to 2 decimal places. Give the result of each iteration to 4 decimal places. [3]
Answer/Explanation
Ans:
4 (i) Make a recognisable sketch of y = ln x
Draw straight line with negative gradient crossing positive y-axis and justify one real root
(ii) Consider sign of ln x = 4 − \(\frac{1}{2}x\) at 4.5 and 5.0 or equivalent
Complete the argument correctly with appropriate calculations
(iii) Use the iterative formula correctly at least once
Obtain final answer 4.84
Show sufficient iterations to justify accuracy to 2 d.p. or show sign change in interval (4.835, 4.845)
Question
(i) Prove that 2 cosec 2θ tan θ ≡ sec2 θ. [3]
(ii) Hence
(a) solve the equation 2 cosec 2θ tan θ = 5 for 0 < θ < π, [3]
(b) find the exact value of \(\int_{0}^{\frac{1}{6}\pi }\) 2 cosec 4x tan 2x dx. [4]
Answer/Explanation
Ans:
6 (i) State or imply \(cosec2\theta=\frac{1}{sin2\theta }\)
Express left-hand side in terms of sinθ and cosθ
Obtain given answer sec2 θ correctly
(ii) (a) State or imply \(cos\theta =\frac{1}{\sqrt{5}}\) or tan θ = 2 at least
Obtain 1.11 or awrt 1.11, allow 0.353π
Obtain 2.03 or awrt 2.03 , allow 0.648π and no other values between 0 and π
(b) State integrand as sec2 2x
Integrate to obtain expression of form k tan mx
Obtain correct \(\frac{1}{2}\) tan 2x
Obtain \(\frac{1}{2}\sqrt{3}\) or exact equivalent
Question
(i) Given that \(\int_{0}^{a}\left ( 3e^{\frac{1}{2}x}+1 \right )dx=10\), show that the positive constant a satisfies the equation [5]
\(a = 2ln\left ( \frac{16-a}{6} \right )\)
(ii) Use the iterative formula \(a_{n+1} = 2ln\left ( \frac{16-a_{n}}{6} \right )\) with a1 = 2 to find the value of a correct to 3 decimal places. Give the result of each iteration to 5 decimal places. [3]
Answer/Explanation
Ans:
5 (i) Obtain integral of form \(ke^{\frac{1}{2}x}+ mx\)
Obtain correct \(6e^{\frac{1}{2}x}+ x\)
Apply limits and obtain correct \(6e^{\frac{1}{2}a}+a-6\)
Equate to 10 and introduce natural logarithm correctly DM1
Obtain given answer \(a=2ln\left ( \frac{16-a}{6} \right )\) correctly
(ii) Use the iterative formula correctly at least once
Obtain final answer 1.732
Show sufficient iterations to justify accuracy to 3 d.p. or show sign change in interval (1.7315, 1.7325)
Question
The diagram shows the curve \(y=x^{4}+2x-9\). The curve cuts the positive x-axis at the point P.
(i) Verify by calculation that the x-coordinate of P lies between 1.5 and 1.6.
(ii) Show that the x-coordinate of P satisfies the equation
\(x=\sqrt[3]{(\frac{9}{x}-2)}\).
(iii) Use the iterative formula
\(x_{n+1}=\sqrt[3]{(\frac{9}{x_{n}}-2)}\).
to determine the x-coordinate of P correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i)Consider sign of \(x^{4}+2x-9 at x = 1.5\) at x=1.5 and x = 1.6
Complete the argument correctly with appropriate calculations
\((f(1.5))=-0.9375,f(1.6)=0.7536\)
(ii) Rearrange \(x^{4}+2x-9=0\) to given equation or vice versa
(iii) Use the iterative formula correctly at least once M1
Obtain final answer 1.56
Show sufficient iterations to justify its accuracy to 2 d.p.

Question
(i) By sketching a suitable pair of graphs, show that the equation
\(\cot x=4x-2\)
where x is in radians, has only one root for \(0\leq x\leq \frac{1}{2}\pi \).
(ii) Verify by calculation that this root lies between x = 0.7 and x = 0.9.
(iii) Show that this root also satisfies the equation
\(x=\frac{1+2\tan x}{4\tan x}\).
(iv) Use the iterative formula \(x_{n+1}=\frac{1+2\tan x_{n}}{4\tan x_{n}}\) to determine this root correct to 2 decimal places.
Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i) Make a recognisable sketch of a relevant graph, e.g. y = cot x or y = 4x – 2
Sketch a second relevant graph and justify the given statement
(ii) Consider sign of 4x – 2 – cot x at x = 0.7 and x = 0.9, or equivalent
Complete the argument correctly with appropriate calculations
(iii) Show that given equation is equivalent to \(x=\frac{1+2\tan x}{4\tan x}\) , or vice versa
(iv) Use the iterative formula correctly at least once M1
Obtain final answer 0.76
Show sufficient iterations to justify its accuracy to 2 d.p. or show there is a sign change
in the interval (0.755, 0.765)
Question
A curve has parametric equations \(x=\frac{1}{(2t+1)^{2}},y=\sqrt{(t+2)}\).
The point P on the curve has parameter p and it is given that the gradient of the curve at P is −1.
(i) Show that \(p=(p+2)^{\frac{1}{6}}-\frac{1}{2}\).
(ii) Use an iterative process based on the equation in part (i) to find the value of p correct to 3 decimalplaces. Use a starting value of 0.7 and show the result of each iteration to 5 decimal places
Answer/Explanation
(i) Obtain derivative of form\( k(2t+1)^{-3}\).
Obtain \(-4(2t+1)^{-3}\) or equivalent as derivative of x .
Obtain \(\frac{1}{2}(t+2)^{-\frac{1}{2}}\) or equivalent as derivative of y
Equate attempt at \(\frac{\mathrm{d} y}{\mathrm{d} x}\) to -1
Obtain \((2p+1)^{3}=8(p+2)^{\frac{1}{2}}\) or equivalent
Confirm given answer \( p=(p+2)^{\frac{1}{6}}-\frac{1}{2}\)
(ii) Use iteration process correctly at least once
Obtain final answer 0.678
Show sufficient iterations to 5 decimal places to justify answer or show a sign change in the interval (0.6775, 0.6785)
[0.7 → 0.68003 → 0.67857 → 0.67847 → 0.6784
Question
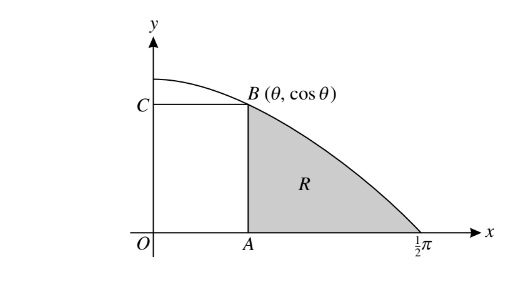
The diagram shows the curve y = cos x, for 0 ≤ x ≤π. A rectangle OABC is drawn, where B is the point on the curve with x-coordinate θ, and A and C are on the axes, as shown. The shaded region R is bounded by the curve and by the lines x = θ and y = 0.
(i) Find the area of R in terms of θ.
(ii) The area of the rectangle OABC is equal to the area of R. Show that \(\Theta =\frac{1-\sin \Theta }{\cos \Theta }\)
(iii) Use the iterative formula \(\Theta _{n+1}=\frac{1-\sin \Theta }{\cos \Theta }\), with initial value θ1= 0.5, to determine the value of θ correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i)Attempt to integrate and use limits θ and π
Obtain 1– sin θ
(ii) State that area of rectangle = θcos θ, equate area of rectangle to area of R
and rearrange to given equation
(iii) Use the iterative formula correctly at least once
Obtain final answer 0.56
Show sufficient iterations to justify its accuracy to 2 d.p. or show there is a
sign change in the interval (0.555, 0.565)