Question
(i) Show that the equation \(log_{10}(x-4)=2-log_{10}x\) can be written as a quadratic equation in x.
(ii) Hence solve the equation \(log_{10}(x-4)=2-log_{10} \) x giving your answer correct to 3 significant figures.
Answer/Explanation
1(i) Use law for the logarithm of a product or quotient
\(Use log_{10}100=2 or 10^{2}=100\)
obtain\( x^{2}-4x-100=0\) , or equivalent
1(ii) Solve a 3-term quadratic equation
Obtain answer 12.2 only
Question
Showing all necessary working, solve the equation ln(2x − 3 )= 2 ln x − ln (x − 1). Give your answer correct to 2 decimal places.
Answer/Explanation
Use law for the logarithm of a product ,quotient or power
Obtain a correct equation free of logarithms
Solve a 3-term quadratic obtaining at least one root
Obtain answer x=4.30 only
Question
It is given that 2 ln(4x − 5 )+ ln(x + 1 )3 ln 3.(i) Show that \(16x^{3}-24x^{2}-15x-2=0\)
(ii) By first using the factor theorem, factorise \(16x^{3}-24x^{2}-15x-2=0\) completely.
(iii) Hence solve the equation 2 ln (4x − 5 )+ ln(x + 1) = 3 ln 3.
Answer/Explanation
(i) Use law for the logarithm for a product or quotient or exponentiation AND for a power
Obtain\( (4x-5)^{2}(x+1)=27\)
Obtain given equation correctly \(16x^{3}-24x^{2}-15x-2=0\)
(ii) Obtain x = 2 is root or (x – 2) is a factor, or likewise with\( x=-\frac{1}{4}\)
Divide by (x – 2) to reach a quotient of the form\((16x^{3}+kx)\)
Obtain quotient \(16x^{3}+8x+1\)
(iii) State x = 2 only
Question
(i) Show that the equation
\(log_{10}\) (x-4)=2-\(log_{10}x\)can be written as a quadratic equation in x.
(ii) Hence solve the equation giving your answer correct to 3 significant figures.
Answer/Explanation
(i) Use law for the logarithm of a product or quotient Use \(log_{10}100=2or 10^{2}=100\)Obtain \(x^{2}-4x-100=0\),or equivalent
(ii) Solve a 3-term quadratic equation Obtain answer 12.2 only
Question
Two variable quantities x and y are believed to satisfy an equation of the form \(y=C(a^{x})\), where C and a are constants. An experiment produced four pairs of values of x and y. The table below gives the corresponding values of x and ln y.
By plotting ln y against x for these four pairs of values and drawing a suitable straight line, estimate the values of C and a. Give your answers correct to 2 significant figures.
Answer/Explanation
2 Plot the four points and draw straight line
State or imply that ln y=ln C+x lna
Carry out a completely correct method for finding lnC or ln a
Obtain answer C = 3.7
Obtain answer a = 1.5
Question
It is given that x = ln (1 − y) − ln y, where 0 < y < 1.
(i) Show that \(y=\frac{e^{-x}}{1+e^{-x}}\).
(ii) Remove logarithms correctly and obtain \(e^{x}=\frac{1-y}{y}\)
(ii) Hence show that \(\int_{0}^{1}ydx=ln(\frac{2e}{e+1})\)
Answer/Explanation
Obtain the given answer \(y=\frac{e^{-x}}{1+e^{x}}\) following full working
3(ii) State integral k ln \((1+e^{-x}) \)where k = ± 1
State correct integral- ln \((1+e^{-x})\)
Use limits correctly D
Obtain the given answer
\(ln\left ( \frac{2e}{e+1} \right )\) following full working
Question
Solve the equation \((1+2^{x})=2\), giving your answer correct to 3 decimal places.
Answer/Explanation
Remove logarithm and obtain \(1+2^{x}=e^{2}\)
Use correct method to solve an equation of the form \(2^{x}\) = a , where a > 0Obtain answer x = 2.676
Question
Solve the equation
log10 (2x + 1) = 2 log10 (x + 1) − 1
Give your answers correct to 3 decimal places. [6]
Answer/Explanation
State or imply 10 log 10 1 = Use law of the logarithm of a power, product or quotient
Obtain a correct equation in any form, free of logs
Reduce to x2 − 18x − 9 = 0, or equivalent
Solve a 3-term quadratic
Obtain final answers x = 18.487 and x = –0.487
Question
Find the set of values of x for which \(2(3^{1-2x})< 5^{x}\). Give your answer in a simplified exact form. [4]
Answer/Explanation
Ans
1 Use law of the logarithm of a product or power
Obtain a correct linear inequality in any form, e.g. ln 2+ (1–2x) ln 3 <x ln 5
Solve for x
Obtain \(x> \frac{ln 6}{ln 45}\)
Question
Solve the equation In 3 + In(2x + 5) = 2 In(2x + 5) = 2 In (x + 2). Give your answer in a simplified exact form.
Answer/Explanation
Ans:
Use law of logarithm of a power and sum and remove logarithms
Obtain a correct equation in any form, e.g. \(3(2x+5)=(x+2)^2\)
Use correct method to solve a 3-term quadratic, obtain at least one root
Obtain final answer final answer \(x=1+2\sqrt{3}\) or \(1+\sqrt{12}\) only
Question
Find the real root of the equation \(\frac{2e^{x}+e^{-x}}{2+e^{x}}=3\), giving your answer correct to 3 decimal places.
Your working should show clearly that the equation has only one real root. [5]
Answer/Explanation
Ans
2 Reduce to a 3-term quadratic u2 + 6u −1= 0 OE
Solve a 3-term quadratic for u
Obtain root \(\sqrt{10}-3\)
Obtain answer x = – 1.818 only
Reject \(-\sqrt{10}-3\) correctly
Alternative method for Question 2
Rearrange to obtain a correct iterative formula
Use the iterative process at least twice
Obtain answer x = – 1.818
Show sufficient iterations to at least 4 d.p. to justify x = – 1.818
Clear explanation of why there is only one real root
Question
Solve the equation \(In(x^3-3)=Inx-In3\). Give your answer correct to 3 significant figures.
Answer/Explanation
Ans:
Use law of the logarithm of a product or power
Obtain a correct equation free of logarithms, e.g. \(3(x^3-3)=x^3\)
Obtain x = 1.65
Question
Solve the equation \((1+2^{x})=2\), giving your answer correct to 3 decimal places.
Remove logarithm and obtain \(1+2^{x}=e^{2}\)
Use correct method to solve an equation of the form \(2^{x}\) = a , where a > 0
Answer/Explanation
Obtain answer x = 2.676
Question
Solve the equation = 8, giving your answer correct to 3 decimal places.
Answer/Explanation
Solve for\(3^{x} \)and obtain\( 3^{x}=\frac{18}{7}\)
Use correct method for solving an equation of the form
Obtain answer x = 0.860 3 d.p. only
Question
Solve the equation ln(x2 + 4) = 2 ln x + ln 4, giving your answer in an exact form. [3]
Answer/Explanation
Ans:
Use law of the logarithm of a power, quotient or product
Remove logarithms and obtain a correct equation in x, e.g. x2 + 4 = 4x2
Obtain final answer x = 2/ √3 , or exact equivalent
Question
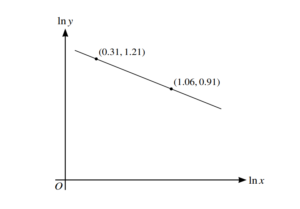
The variables x and y satisfy the equation xny2 = C, where n and C are constants. The graph of ln y against ln x is a straight line passing through the points (0.31, 1.21) and (1.06, 0.91), as shown in the diagram.
Find the value of n and find the value of C correct to 2 decimal places.
Answer/Explanation
Ans:
State or imply n In x + 2 In y = In C
Substitute values of ln y and ln x, or equate gradient of line to \(\pm \frac{1}{2}n\) but not ±n, and solve for n
Obtain n = 0.8[0] or 0.8[00] or \(\frac{4}{5}\)
Solve for C
Obtain C = 14.41
Question
Solve the equation
\(5^{x−1} \)=\( 5^{x }− 5\),
giving your answer correct to 3 significant figures.
Answer/Explanation
EITHER Use laws of indices correctly and solve for 5^{x} or for \( 5^{–x}\)
or for \(5^{x–1}\)
Obtain\( 5^{x}\)
or for\( 5^{–x}\)
or for\( 5 ^{x–1}\)
in any correct form, e.g. \(5^{x}\)\( \frac{5}{1-\frac{1}{5}}\)
Use correct method for solving \(5^{x}\) = a, or \(5^{–x} \) = a, or \(5^{x–1}\) = a, where a 0 Obtain answer x = 1.14
OR Use an appropriate iterative formula, \(x_{n+1}\)=\(\frac{In(5^{x-1+5})} {In5} \)correctly, at least once
Obtain answer 1.14
Obtain answer 1.14
Show sufficient iterations to at least 3 d.p. to justify 1.14 to 2 d.p., or show there is a sign change in the interval (1.135, 1.145) Show there is no other root [For the solution x = 1.14 with no relevant working give , and a further B1 if
1.14 is shown to be the only solution.]
Question
The polynomial p(x) is defined by\(p(x)=x^{3}-3ax+4a\),where a is a constant.
(i) Given that (x − 2) is a factor of p(x), find the value of a.
(ii) When a has this value,
(a) factorise p(x)completely,
(b) find all the roots of the equation\( p(x^{2})\)=0
Answer/Explanation
(i) Substitute x = 2 and equate to zero, or divide by x – 2 and equate constant remainder to zero, or equivalent
Obtain a = 4
(ii) (a) Find further (quadratic or linear) factor by division, inspection or factor theorem or equivalent
Obtain x^{2}+ 2x – 8 or x + 4
State (x – 2)^{2}
(x + 4) or equivalent
(b) State any two of the four (or six) roots
State all roots \((\pm \sqrt{2},\pm 2i) \)provided two are purely imaginary