Question
(i) Show that the equation \((\sqrt{2})cosecx+cotx =\sqrt{3}\)can be expressed in the form Rsin(x-\alpha )=\sqrt{2} where R > 0 and \(0Å < \alpha< 90Å.\) [4]
(ii) Hence solve the equation\( (\sqrt{2})\) cosec x + cot x = ï3, for 0Å < x < 180Å. [4]
Answer/Explanation
(i) Rearrange in the form State R =\( \sqrt{3}sinx-cox=\sqrt{2}\)
Use trig formulae to obtain α
Use trig formulae to obtain α
(ii) Evaluate\( sin^{-1}\left ( \frac{\sqrt{2}}{R} \right )\) Carry out a correct method to find a value of x in the given interval
Obtain answer x = 75°
Obtain a second answer e.g. x = 165° and no others
[Treat answers in radians as a misread. Ignore answers outside the given interval.]
Question
(i) By first expanding cos(2x + x), show that \(cos 3x \equiv 4cos^{3}x-3cosx\)
(ii) Hence solve the equation cos 3x + 3 cos x + 1 = 0, for 0 ≤ x ≤ \Pi.
(iii) Find the exact value of \(\int _{\frac{1}{6}\Pi }^{\frac{1}{3}\Pi }cos^{3}x dx\)
Answer/Explanation
(i) Use cos(A +B) formula to express cos3x in terms of trig functions of 2x and x Use double angle formulae and Pythagoras to obtain an expression in terms of cos x
only
Obtain a correct expression in terms of cos x in any form
Obtain \(cos3x= 4cos^{3}x-3cosx\)
(ii) Use identity and solve cubic \(4cos^{3}x=-1\) for x
Obtain answer 2.25 and no other in the interval
(iii) Obtain indefinite integral \(\frac{1}{12}sin3x+\frac{3}{4}sinx\)
Substitute limits in an indefinite integral of the form a xb x sin 3 sin + , where ab ≠ 0
Obtain answer \(\frac{1}{24}(\sqrt[9]{3-11})\) , or exact equivalent
Alternative method for question (iii)
\(\int cosx(1-sin^{2}x)dx=sinx-\frac{1}{3}sin^{3}x(+C)\)
Substitute limits in an indefinite integral of the form\( asinx+bsin^{3}x \)where ab ≠ 0
Obtain answer \( \frac{1}{24}(\sqrt[9]{3}-11)\) , or exact equivalent
Question
By first expressing the equation cot 1 −\( cot\Theta -cot(\Theta +45 )\)= 3 as a quadratic equation in tan 1, solve the equation for 0Å < 1 < 180Å.
Answer/Explanation
Use correct trig formula and obtain an equation in \( \tan \Theta \)
Obtain a correct horizontal equation in any form
Reduce to
Question
(i) Given that \(sin(\theta+45^{\circ})+2cos(\theta+60^{\circ})\) find the exact value of \(tan\theta \) in a form involving surds. You need not simplify your answer.
(ii) Hence solve the equation \(sin(\theta+45^{\circ})+2cos(\theta+60^{\circ})=3cos\theta \) for \(0^{\circ}<\theta <360^{\circ}\)
Answer/Explanation
(i)
Use trig formulae and obtain an equation in sin θ and cosθ M1 Obtain a correct equation in any form A1 Substitute exact trig ratios and obtain an expression for tanθ Obtain answer \(tanθ =\frac{\sqrt[2]{2}-1}{1-\sqrt{6}}\) , or equivalent
(ii)
State answer, e.g. θ = 128.4° B1 State second answer, e.g.θ = 308.4°
Question
(i) Simplify\( sin2\alpha sec\alpha \)
(ii) Given that\( 3 cos2\beta +7cos\beta =0\), find the exact value of\( cos\beta \).
Answer/Explanation
(i) State sin2α = 2sinα cosα and secα = 1/cosα
Obtain 2sinα
(ii) Use cos2β = \(2cos^{2}\beta -1\) or equivalent to produce correct equation in cosβ
Solve three-term quadratic equation for cosβ
Obtain \(cos β \frac{1}{3}only\)
Question
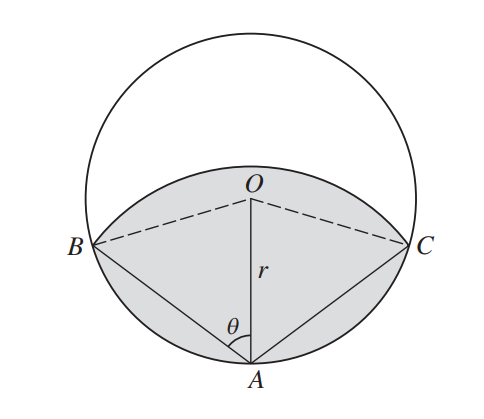
In the diagram, A is a point on the circumference of a circle with centre O and radius r. A circular arc with centre A meets the circumference at B and C. The angle OAB is θ radians. The shaded region is bounded by the circumference of the circle and the arc with centre A joining B and C. The area of the shaded region is equal to half the area of the circle.
(i) Show that \(cos2\theta =\frac{2sin2\theta -\pi }{4\theta}\). [5]
(ii) Use the iterative formula \(\theta _{n+1}=\frac{1}{2}cos^{-1}\left ( \frac{2sin2\theta_{n}-\pi}{4\theta_{n}} \right ),\)
with initial value θ1= 1, to determine θ correct to 2 decimal places, showing the result of each iteration to 4 decimal places. [3]
Answer/Explanation
Ans:
(i) State or imply AB = 2r cosθ or AB2 = 2r2 – 2r2 cos(π-2θ)
Use correct formula to express the area of sector ABC in terms of r and θ
Use correct area formulae to express the area of a segment in terms of r and θ
State a correct equation in r and θ in any form
Obtain the given answer
[SR: If the complete equation is approached by adding two sectors to the shaded area above BO and OC give the first M1 as on the scheme, and the second M1 for using correct area formulae for a triangle AOB or AOC, and a sector AOB or AOC.]
(ii) Use the iterative formula correctly at least once
Obtain final answer 0.95
Show sufficient iterations to 4 d.p. to justify 0.95 to 2 d.p., or show there is a sign change in the interval (0.945, 0.955)
Question
(i) Express 4 cos θ + 3 sin θ in the form R cos(θ − α), where R > 0 and 0 < α <\(\frac{1}{2}\pi \) . Give the value of α correct to 4 decimal places. [3]
(ii) Hence
(a) solve the equation 4 cos θ + 3 sin θ = 2 for 0 < θ < 2π, [4]
(b) find \(\int \frac{50}{\left ( 4cos\theta +3sin \theta\right )^{2}}d\theta .\)[3]
Answer/Explanation
Ans:
(i) State or imply R = 5
Use relevant trigonometry to find α
Obtain α = 0.6435
(ii) (a) Carry out appropriate method to find one value in given range
Obtain 1.80
Carry out appropriate method to find second value in given range
Obtain 5.77 and no other value
(b) Express integrand as k sec2 ( θ – their α) for any constant k
Integrate to obtain result k tan ( θ – their α)
Obtain correct answer 2 tan( θ – 0.6435)
Question
(i) Prove the identity \(tan(45^{\circ} + x) + tan(45^{\circ} − x)\equiv 2 sec 2x\).
(ii) Hence sketch the graph of \(y=tan(45^{\circ}+x)+tan(45^{\circ}-x) for 0^{\circ}\leqslant x\leqslant 90^{\circ}\).
Answer/Explanation
4(i) Use correct tan( A ±B) formula and express the LHS in terms of tan x
Using tan 45 ° = 1express LHS as a single fraction
Use Pythagoras or correct double angle formula
Obtain given answer
4(ii) Show correct sketch for one branch Both branches correct and nothing else seen in the interval
Show asymptote at x = 45°
Question
(i) By first expanding 2 sin(x − 30Å), express 2 sin(x − 30Å) − cos x in the form \(Rsin(x-\alpha )\), where R > 0 and 0Å <\( \alpha\) < 90Å. Give the exact value of \(\alpha\)R and the value of \(\alpha\) correct to 2 decimal places.
(ii) Hence solve the equation
2 sin(x − 30Å )− cos x =1
for 0Å < x < 180Å.
Answer/Explanation
8(i) Use sin(A-B ) formula and obtain an expression in terms of sin x and cos x
Collect terms and reach \(\sqrt{3}sinx-2cos\), or equivalent
Obtain R = \( \sqrt{7}\)
Use trig formula to find α
Obtain α = 49.11° with no errors seen
8(ii) \(sin^{-1}(1/\sqrt{7})\) to at least 1 d.p. (22.21° to 2 d.p.) FT
Use a correct method to find a value of x in the interval 0° < x < 180°
Obtain answer 71.3°
[ignore answers outside given range.]
Question
The parametric equations of a curve are \(x=lncos\theta, y=3\theta-tan\theta,\)
where \(0\leqslant \Theta < \frac{1}{2}\pi\) .
(i) Exprexx \(\frac{dy}{dx}\) in \(termx of tan\Theta \).
(ii) Find the exact y-coordinate of the point on the curve at which the gradient of the normal is equal to 1.
Answer/Explanation
State
\(\frac{dy}{d\Theta }=3-sec^{2}\Theta \)
Use\(\frac{dy}{dx}=\frac{dy}{d\Theta }\div \frac{dx}{d\Theta }\)
Obtain correct \(\frac{dy}{dx} in any form e.g.\frac{3-sec^{2}\Theta }{-tan\Theta }\)
Obtain\(\frac{dy}{dx} =\frac{tan^{2}\Theta -2}{-tan\Theta } \)or equivalent
4(ii) Equate gradient to −1 and obtain an equation in tanθ
Solve a 3 term quadratic \(\left ( tan^{2}\Theta +tan\Theta -2=0 \right )\)
Obtain \(\Theta =\frac{\pi }{4}and y=\frac{3\pi }{4}-1\) only
Question
(i) Express\( 8cos\Theta -15sin\Theta\) in the form \(Rcos(\Theta +\alpha )\), where R > 0 and 0Å < \(\Theta\)< 90Å, stating the
exact value of R and giving the value of ! correct to 2 decimal places.
(ii) Hence solve the equation
8 cos 2x − 15 sin 2x = 4,for 0Å < x < 180Å.
Answer/Explanation
(i) State R = 17
Use trig formula to find α
Obtain α = 61.93° with no errors seen
(ii) Evaluate \(cos^{-1}(4/17)\) to at least 1d.p. (76.39° to 2 d.p.)
Use a correct method to find a value of x in the interval 0° < x < 180°
Obtain answer, e.g. x = 7.2°
Obtain second answer, e.g. x = 110.8°and no others
[Ignore answers outside the given interval.]
[Treat answers in radians as a misread.]
Question
(a) Express \(\sqrt{6}\cos \theta +3\sin \theta\) in the form \(R\cos (\theta -\alpha ) , \ where \ R> 0 \ and \ 0^{o}< \alpha < 90^{o}\). State the exact
value of R and give \(\alpha\) correct to 2 decimal places. [3]
(b) Hence solve the equation \(\sqrt{6}\cos \frac{1}{3}x+3\sin \frac{1}{3}x=2.5, \ for \0^{o}< x< 360^{o}\) [4]
Answer/Explanation
Ans
( a) State \(R=\sqrt{15}\)
Use trig formulae to find \(\alpha \)
Obtain α = 50.77
(b) Evaluate \(\beta =\cos ^{-1}\frac{2.5}{\sqrt{15}}(49.797^{o}\ to \ 4 d.p.)\)
Use correct method to find a value of \(\frac{x}{3}\) in the interval
Obtain answer rounding to x = 301.6° to 301.8° A1
Obtain second answer rounding to x = 2.9(0)° to 2.9(2)° and no
others in the interval
Question
Express the equation tan (θ + 60o) = 2 + tan (60o − θ) as a quadratic equation in tan θ , and hence solve the equation for 0o ≤ θ ≤ 180o.
Answer/Explanation
Use tan (A ± B) formula and obtain an equation in tan θ
Using \(\tan 60^{o}=\sqrt{3}\), obtain a horizontal equation in tan θ in any correct form
Reduce the equation to 3 tan2 θ + 4 tan θ – 1 = 0, or equivalent
Solve a 3-term quadratic for tan θ
Obtain a correct answer, e.g. 12.1°
Obtain a second correct answer, e.g. 122.9°, and no others in the given interval
Question
(a) Show that \(\frac{cos 3x}{sin x} + \frac{sin 3x}{cos x} = 2 cot 2x\).
(b) Hence solve the equation \(\frac{cos 3x}{sin x}+\frac{sin 3x}{cos x}=4\), for 0<x<\(\pi\).
Answer/Explanation
Ans:
(a) Express LHS correctly as a single fraction
Use cos(A\(\pm\)B)\) formula to simplify the numerator
Use sin 2A formula to simplify the denominator
Obtain the given result.
(b) Obtain an equation in tan 2x and use correct method to solve for x
Obtain answer, e.g. 0.232
Obtain second answer, e.g. 1.80
Question
(a)Express 5 sin x − 3 cos x in the form R sin (x-α), where R> 0 and 0< α < \(\frac{1}{2}\pi \) . Give the exact value of R and give ! correct to 2 decimal places.
(b)Hence state the greatest and least possible values of (5 sin x − 3 cos x)2.
Answer/Explanation
Ans:
(a)State R = \(\sqrt{34}\)
Use trig formulae to find α
Obtain α = 0.54
(b)
State greatest value 34
State least value 0
Question
(a) Prove that \(\frac{1-\cos 2\theta }{1+\cos 2\theta }=\tan ^{2}\theta\) [2]
(b) Hence find the exact value of \(\int_{\frac{1}{6}\pi }^{\frac{1}{3}\pi } \frac{1-\cos 2\theta }{1+\cos 2\theta }\) [4]
Answer/Explanation
Ans
4 (a) Use correct double angle formula or t-substitution twice
Obtain \( \frac{1-\cos 2\theta }{1+\cos 2\theta }=tan^{2}\theta\) from correct working
4 (b) Express 2 tanθ in terms of 2 secθ
Integrate and obtain terms tanθ – θ
Substitute limits correctly in an integral of the form a tanθ + bθ , where ab≠0
Obtain answer \(\frac{2}{3}\sqrt{3}-\frac{1}{6}\pi \)
Question
(a) Given that cos(x − 30) = 2 sin (x + 30), show that \(\tan x=\frac{2-\sqrt{3}}{1-2\sqrt{3}}\) [4]
(b) Hence solve the equation
cos(x − 30o) = 2 sin(x + 30o),
for 0o < x < 360o [2]
Answer/Explanation
Ans
(a) Use correct trig expansions and obtain an equation in sin x and cos x
Use correct exact trig ratios for 30° in their expansion
Obtain an equation in tan x
Obtain \(\tan x=\frac{2-\sqrt{3}}{1-2\sqrt{3}}\) from correct working
(b) Obtain answer in the given interval, e.g.173.8 °
Obtain a second answer and no other in the given interval, e.g. 353.8 °
Question
(a) Express \(\sqrt{7} sin x + 2cos x\) in the form \(R sin(x+\alpha)\), where R>0 and \(0^o<\alpha<90^o\). State the exact value of R and give \(\alpha\) correct to 2 decimal places.
(b) Hence solve the equation \(\sqrt{7}sin 2\theta + 2 cos 2\theta =1\), for \(0^o<\theta<180^o\).
Answer/Explanation
Ans:
- State \(R=\sqrt{11}\)
Use trig formulae to find \(\alpha\)
Obtain \(\alpha =37.09^o\) - Evaluate \(sin^{-1}(\frac{1}{\sqrt{11}})\) to at least 2 dp \((17.5484^o)\)
Use correct method to find a value of \(\theta\) in the interval
Obtain answer, e.g. \(\62.7^o\)
Obtain second answer, e.g. \(170.2^o\), and no other in the interval
Question
By first expressing the equation \(tan(x+45^o)=2cotx+1\) as a quadratic equation in tan x, solve the equation for \(0^o<x<180^o\).
Answer/Explanation
Ans:
Use correct trig formulae to obtain an equation in tan x
Using \(tan45^o=1\), obtain a horizontal equation in tan x in any form
Reduce the equation to \(tan^2x+tan x-1=0\), or 3-term equivalent
Solve a 3-term quadratic in tan x, for x
Obtain answer, e.g. \(x=31.7^o\)
Obtain second answer, e.g. \(x=121.7^o\), and no other in the interval
Question
(i) Prove the identity tan \(tan2\Theta -tan\Theta sec2\Theta \)
(ii) Hence show that \(\int_{0}^{\frac{1}{6}\pi }tan\Theta sec2\Theta d\Theta =\frac{1}{2}In\frac{3}{2}\)
Answer/Explanation
(i) EITHER: Use tan 2A formula to express LHS in terms of tanθ Express as a single fraction in any correct form Use Pythagoras or cos 2A formula Obtain the given result correctly
OR: Express LHS in terms of sin 2θ, cos 2θ, sin θ and cosθ
Express as a single fraction in any correct form
Use Pythagoras or cos 2A formula or sin(A – B) formula Obtain the given result correctly
(ii) Integrate and obtain a term of the form aln(cos2 ) θ or bln(cos ) θ (or secant equivalents)
Obtain integral \(-\frac{1}{2}\) ln(cos 2 θ ) ln(cos θ ) , or equivalent
Substitute limits correctly (expect to see use of both limits)
Obtain the given answer following full and correct working
Question
Express the equation sec θ = 3 cos θ+ tan θ as a quadratic equation in sin 1. Hence solve this equation for \(-90^{\circ}< \Theta < 90^{\circ}\)
Answer/Explanation
.
EITHER: Correctly restate the equation in terms ofsinθ and cosθ
Correct method to obtain a horizontal equation insinθ
Reduce the equation to a correct quadratic in any form, e.g.\( 3sin^{2}\Theta -sin\Theta -2=0\)
Solve a three-term quadratic forsinθ Obtain final answer θ =−41.8° only
[Ignore answers outside the given interval.]
OR 1: Square both sides of the equation and use \(1+tan^{2}\Theta =sec^{2}\Theta \)
Correct method to obtain a horizontal equation insinθ
Reduce the equation to a correct quadratic in any form, e.g. \(9sin^{2}–6sin\Theta -8=0\)
Solve a three-term quadratic for sinθ
Obtain final answer θ = −41.8° only
OR 2: Multiply through by (secθ + tanθ)
Use \(sec^{2}\Theta -tan^{2}\Theta =1\)
Obtain 1 = 3 + 3sinθ
Solve for sinθ
Obtain final answer θ = −41.8° only
Question
By expressing the equation cosec θ = 3 sin θ+ cot θ in terms of cos 1 only, solve the equation for \(0^{\circ}<\Theta <180^{\circ}\).
Answer/Explanation
Correctly restate the equation in terms of sin θ and cos θ
Using Pythagoras obtain a horizontal equation in cos θ
Reduce the equation to a correct quadratic in cos θ, e.g . \(3cos^{2}\Theta -cos\Theta -2=0\)
Solve a 3-term quadratic for cos θ
Obtain answer θ = 131.8° only
[Ignore answers outside the given interval.]
Question
Express the equation tan(θ + 45°) − 2 tan(θ + 45°) = 4 as a quadratic equation in tan θ. Hence solve this equation for 0° ≤ 1 ≤ 180°.[6]
Answer/Explanation
Ans:
Use tan(A ± B) formula and obtain an equation in tan θ
Using tan 45° = 1, obtain a horizontal equation in tan θ in any correct form
Reduce the equation to 7 tan2 θ – 2 tan θ – 1, or equivalent
Solve a 3-term quadratic for tan θ
Obtain a correct answer, e.g. θ = 28.7°
Obtain a second answer, e.g. θ = 165.4° , and no others
[Ignore answers outside the given interval. Treat answers in radians as a misread (0.500, 2.89).]
Question
(i) By differentiating \(\frac{1}{cosx}\) , show that if y = sec x then\( \frac{dy}{dx}\) = sec x tan x.
(ii) Show that \(\frac{1}{(secx-tanx)}\) = sec x + tan x.
(iii) Deduce that \(\frac{1}{(secx-tanx)^{2}}\) = \(2 sec^{2}\)
x − 1 + 2 sec x tan x.
(iv) Hence show that \(\int_{0}^{\frac{1}{4}\pi }\frac{1}{(secx-tanx)^{2}}dx\)=\(\frac{1}{4}(8\sqrt{2}-\pi )\)
Answer/Explanation
(i) Use correct quotient or chain rule Obtain the given answer correctly having shown sufficient working
(ii) Use a valid method, e.g. multiply numerator and denominator by sec x + tan x, and a version of Pythagoras to justify the given identity
(iii) Substitute, expand
(sec x +\( tan x)^{2}\)
and use Pythagoras once
Obtain given identity
(iv) Obtain integral 2 tan x – x + 2 sec x
Use correct limits correctly in an expression of the form a tan x + bx + c sec x, or
equivalent, where abc 0
Obtain the given answer correctly

Question
Solve the equation
sin(θ + 45◦) = 2 cos(θ − 30◦),
giving all solutions in the interval 0◦ < θ < 180◦.
Answer/Explanation
Attempt use of sin (A + B) and cos (A – B) formulate to obtain an equation in cos θ and sin θ
Obtain a correct equation in any form
Use trig. formula to obtain an equation in tan θ (or cos θ, sin θ or cot θ)
Obtain tan θ \(\frac{\sqrt{6}-1}{1-\sqrt{2}}\) , or equivalent (or find cost θ, sin θ or cot θ)
Obtain answer θ = 105.9°, and no others in the given interval
[Ignore answers outside the given material]
Question
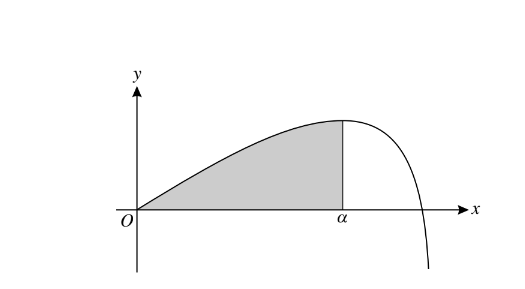
The diagram shows the curve y\(=8sin\frac{1}{2}x-tan\frac{1}{2}x\) for 0 ≤ x < π. The x coordinate of the maximum point is α and the shaded region is enclosed by the curve and the lines x = α and y = 0.
(i) Show that\( α \frac{2}{3}\pi \)
(ii) Find the exact value of the area of the shaded region.
Answer/Explanation
(i) Differentiate to obtain \(4cos\frac{1}{2}x-\frac{1}{2}sec^{2}\frac{1}{2}x\)
Equate to zero and find value of \(cos\frac{1}{2}x\)
Obtain \( cos\frac{1}{2}x=\frac{1}{2} \) and confirm \(\alpha =\frac{2}{3}\pi\)
(ii) Integrate to obtain \(-16cos\frac{1}{2}x\)
\(+2Incos\frac{1}{2}x \)or equivqlent
Using limits 0 and \(\frac{2}{3}\pi in acos\frac{1}{2}x+bIncos\frac{1}{2}x\)
Obtain\( 8+2In\frac{1}{2}\) or exact equivalent