Question
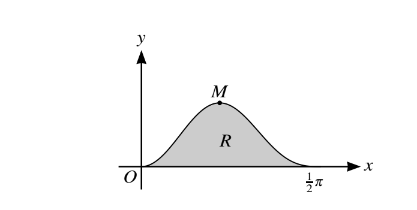
The diagram shows the curve\( y = 5sin^{2}xcox^{3}x \) for\( 0 ≤ x ≤\frac{1}{2}\pi \) , and its maximum point M. The shaded region R is bounded by the curve and the x-axis.
(i) Find the x-coordinate of M, giving your answer correct to 3 decimal places. [5]
(ii) Using the substitution u = sin x and showing all necessary working, find the exact area of R. [4]
Answer/Explanation
(i) Use product rule
Obtain correct derivative in any form Equate derivative to zero and obtain an equation in a single trig function
Obtain a correct equation, e.g.
Obtain answer x = 0.685
(ii) Use the given substitution and reach\( a\int (u^{2}-u^{4})du\) Obtain correct integral with a = 5 and limits 0 and 1
Use correct limits in an integral of the form \(a\left ( \frac{1}{3} u^{3}-\frac{1}{5}u^{5}\right )\)
Obtain answer \(\frac{2}{3}\)
Question
The parametric equations of a curve are
x = 2 sin 1 + sin 21, y = 2 cos 1 + cos 21, where 0 < 1 < 0.
(i) Obtain an expression for\(\frac{dy}{dx} \) in terms of \(\Theta \)
(ii) Hence find the exact coordinates of the point on the curve at which the tangent is parallel to the
y-axis.
Answer/Explanation
4(i) \(obtain \frac{dx}{d\Theta }=2cos\Theta +2cos2\Theta or \frac{dy}{d\Theta }=-2sin\Theta -2sin2\Theta\)
use\( dy/dx=dy/d\Theta \div dx/d\Theta\)
Obtain correct\( \frac{dy}{dx}e.g.-\frac{2sin\Theta +2sin2\Theta }{2cos\Theta +2cos2\Theta }\)
4(ii) Equate denominator to zero and use any correct double angle formula
Obtain correct 3-term quadratic in cosθ in any form Solve forθ
Obtain\( x = \sqrt[3]{3} and y=\frac{1}{2} y = 1\) 2 , or exact equivalents
Question
The parametric equations of a curve are
x = 2t + sin 2t, y = ln(1 − cos 2t). Show that\( \frac{dy}{dx}\)= cosec 2t
Answer/Explanation
.State \(\frac{dx}{dt}=2+2 cos2t\) Use the chain rule to find the derivative of y
Obtain \(\frac{dy}{dt}=\frac{2sin2t}{1-cos2t}\)
Use \(\frac{dy}{dx}=\frac{dy}{dt}\div \frac{dx}{dt}\)
Obtain \(\frac{dy}{dx}\) t x
= correctly
Question
Find the gradient of the curve \(x^{3}+3xy^{2}-y^{3}\)=1
at the point with coordinates(1, 3).
Answer/Explanation
State or imply \(3y^{2}+6xy\frac{\mathrm{d} y}{\mathrm{d} x}\) as derivative of \(3xy^{2}\)
State or imply \(3y^{2}\frac{\mathrm{d} y}{\mathrm{d} x}\) as derivative of \(y^{3}\)
Equate derivative of LHS to zero ,substitute(1,3) and find the gradient
Obtain final answer \(\frac{10}{3}\) or equivalent
Question
The variables x and y satisfy the relation sin y = tan x, where\( -\frac{1}{2}\Pi<y<\frac{1}{2}\Pi\) show that\( \frac{dy}{dx}=\frac{1}{cosx\sqrt{(cos2x)}}\)
Answer/Explanation
State \((cos)y\frac{dy}{dx}\) as derivative of siny State correct derivative in terms of and y and y,e.g\(sec^{2}x/cos y\) State correct derivative in terms of
\(x,e.g\frac{sec^{2}x}{\sqrt{1-tan^{2}x}}\) Use double angle formula Obtain the given answer correctly
Question
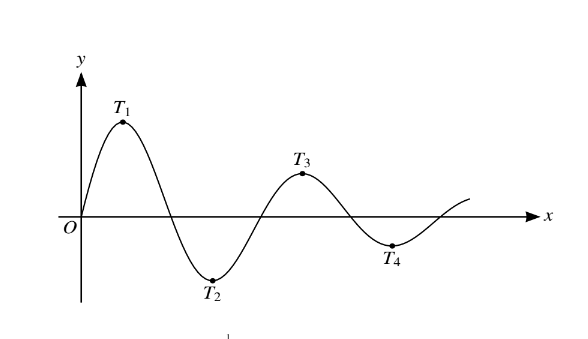
The diagram shows the curve y =\( 10e^{-\frac{1}{2}x} \)xsin 4x for x ≥ 0. The stationary points are labelled T1 , T2 ,
(i) Find the x-coordinates of T1 and T2 , giving each x-coordinate correct to 3 decimal places.
(ii) It is given that the x-coordinate of Tn is greater than 25. Find the least possible value of n.
Answer/Explanation

Question
The parametric equations of a curve are
x = ln(2t + 3), \(x=In(2t+3),y=\frac{3t+2}{2t+3}\)
Find the gradient of the curve at the point where it crosses the y-axis
Answer/Explanation
.
Obtain for derivative of x
Use quotient of product rule, or equivalent, for derivative of y
Obtain or unsimplified equivalent
Obtain t = –1
Use in algebraic or numerical form
Obtain gradient
Question
The equation of a curve is \(y=\frac{1+\times }{1+2x} for \times> -\frac{1}{2}\) . Show that the gradient of the curve is always negative. [3]
Answer/Explanation
Ans:
Use correct quotient or product rule
Obtain correct derivative in any form
Justify the given statement
Question
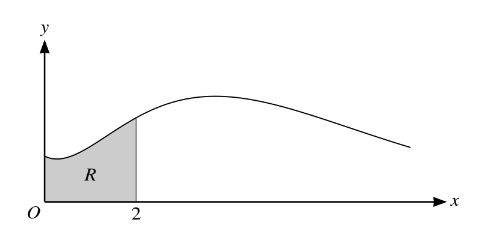
The diagram shows the curve y =\((1+x^{2})e^{-\frac{1}{2}} for x\geqslant 0.\) for x ≥ 0. The shaded region R is enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
(i) Find the exact values of the x-coordinates of the stationary points of the curve.
(ii) Show that the exact value of the area of R is \(18-\frac{42}{e}\)
Answer/Explanation
9(i) Use correct product or quotient rule
Obtain correct derivative in any form
Equate derivative to zero and obtain a 3 term quadratic equation in x
Obtain answer \(x=2\pm \sqrt{3} \)
9(ii) Integrate by parts and reach\(k(1+x^{2})e^{\frac{-1}{2}x}+l\int se^{\frac{-1}{2}x}dx\),
Obtain \(-2(1+x^{2})e^{\frac{-1}{2}x}+4\int se^{\frac{-1}{2}x}dx\) or equivalent
Complete the integration and obtain \((-18-8x-2x^{2})e^{\frac{-1}{2}x}\) , or equivalent
Use limits x = 0 and x = 2 correctly, having fully integrated twice by parts
Obtain the given answer
Question
The equation of a curve is \(2x^{4} + xy^{3} + y^{4}\) = 10.
(i) Show that\(\frac{dy}{dx}=-\frac{8x^{3}+y^{3}}{3xy^{2}+4y^{3}}\).
(ii) Hence show that there are two points on the curve at which the tangent is parallel to the x-axis and find the coordinates of these points.
Answer/Explanation
State or imply\(y^{3}+3xy^{2}\frac{dy}{dx}\) as derivative of \(xy^{3}\)
State or imply \(4y^{3}\frac{dy}{dx} y^{4}\) as derivative of \(y^{4}\)
Equate derivative of the LHS to zero and solve for\(\frac{dy}{dx}\)
Obtain the given answer
5(ii) Equate numerator to zero
Obtain y = −2x, or equivalent
Obtain an equation in x or y DM1
Obtain final answer x = −1, y = 2 and x = 1, y = −2
Question
The curve with equation \(y =e^{-ax}\) tan x, where a is a positive constant, has only one point in the interval \(0<x<\frac{1}{2}\pi \)at which the tangent is parallel to the x-axis. Find the value of a and state the exact value
of the x-coordinate of this point.
Answer/Explanation
Use product rule
Obtain correct derivative in any form
Equate derivative to zero, use Pythagoras and obtain a quadratic equation in tan x
Obtain\( tan^{2}x-a tanx+1=0\), or equivalent
Use the condition for a quadratic to have only one root
Obtain answer a = 2
Obtain answer x=\(\frac{1}{4}\pi \)
Question
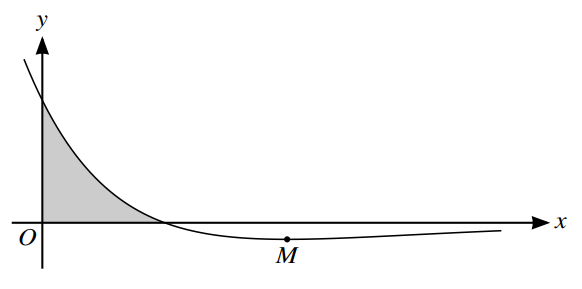
The diagram shows the curve \(7=(2-x)e^{-\frac{1}{2}x}\), and its minimum point M.
(a) Find the exact coordinates of M. [5]
(b) Find the area of the shaded region bounded by the curve and the axes. Give your answer in terms
of e. [5]
Answer/Explanation
(a) Use correct product or quotient rule
Obtain correct derivative in any form
Equate derivative to zero and solve for x D
Obtain x = 4 A1 ISW
Obtain y = –2e–2, or exact equivalent
(b) Commence integration and reach
\(a(2-x)e^{-\frac{1}{2}x}+b\int e^{-\frac{1}{2}x}dx\)
Obtain \(-2(2-x)e^{-\frac{1}{2}x}-2\int e^{-\frac{1}{2}x}dx\)
Complete integration and obtain \(2xe^{-\frac{1}{2}x}\)
Use correct limits, x = 0 and x = 2, correctly, having integrated
twice
Obtain answer 4e–1, or exact equivalent
Alternative method for question (b)
\(\frac{d\left ( 2xe^{-\frac{1}{2}x} \right )}{dx}=2e^{-\frac{1}{2}x}-xe^{-\frac{1}{2}x}\)
∴\(2xe^{-\frac{1}{2}x}\)
Use correct limits, x = 0 and x = 2, correctly, having integrated
twice
Obtain answer 4e–1, or exact equivalent
Question
The parametric equations of a curve are
x = 3 − cos 2 θ, y = 21 + sin 2 θ,
\(for \ 0< \theta < \frac{1}{2}\pi\)
Show that \(\frac{dy}{dx}=\cot \theta \) [5]
Answer/Explanation
State or imply \(\frac{dx}{d\theta }=2\sin 2\theta \ or \ \frac{dy}{d\theta }=2+2\cos 2\theta\)
Use \(\frac{dy}{dx}=\frac{dy}{d\theta }\div \frac{dx}{d\theta } \)
Obtain correct answer \(\frac{dy}{dx}=\frac{2+2\cos 2\theta }{2\sin 2\theta }\)
Use correct double angle formulae
Obtain the given answer correctly \(\frac{dy}{dx}=\cot \theta \)
Alternative method for question
Start by using both correct double angle formulae
e.g. x = 3 – (2cos2θ − 1), y = 2 θ + 2sin θ cos θ
\(\frac{dx}{d\theta } \ or \ \frac{dy}{d\theta }\)
\(\frac{dy}{dx}=\frac{(2+2(\cos ^{2}\theta -\sin 2\theta ))}{4\cos \theta \sin \theta }\)
Simplify to given answer correctly \(\frac{dy}{dx}=\cot \theta \)
3 Alternative method for question 3
\(Set=2\theta .\ State\frac{dx}{dt}=\sin t\ or\ \frac{dy}{dt}=1+\cos t\)
\(Use\ \frac{dy}{dx}=\frac{dy}{dt}\div \frac{dx}{dt}\)
Obtain correct answer \(\frac{dy}{dx}=\frac{1+\cos t}{\sin t}\)
Use correct double angle formulae
Obtain the given answer correctly \(\frac{dy}{dx}=\cot \theta\)
Question
Let \(f(x)=\frac{\cos x}{1+\sin x}\)
(a) Show that f′x < 0 for all x in the interval \(-\frac{1}{2}\pi < x< \frac{3}{2}\pi\)
(b) Find \(\int_{\frac{1}{6}\pi }^{\frac{1}{2}\pi }f(x)dx \). Give your answer in a simplified exact form.
Answer/Explanation
Ans
(a) Use quotient or product rule
Obtain derivative in any correct form e.g \(\frac{-\sin x(1+\sin x)-\cos x(\cos x)}{(1+\sin x)^{2}}\)
Use Pythagoras to simplify the derivative
Justify the given statement
(b) State integral of the form a ln (1 + sin x)
State correct integral ln (1 + sin x) A1
Use limits correctly
Obtain answer \(ln\frac{4}{3}\)
Question
The curve with equation y = e2x (sin x + 3 cos x) has a stationary point in the interval 0 ≤ x ≤ π.
(a) Find the x-coordinate of this point, giving your answer correct to 2 decimal places. [4]
(b) Determine whether the stationary point is a maximum or a minimum. [2]
Answer/Explanation
(a) Use product rule
Obtain derivative in any correct form e.g. \(2e^{2x}(\sin x+3\cos x)+e^{2x}(\cos x-3\sin x)\)
Equate derivative to zero and obtain an equation in one trigonometric ratio
Obtain x = 1.43 only
(b) Use a correct method to determine the nature of the stationary point
\(x=1.42,y’=0.06e^{2.84}> 0\)
e.g.
\(x=1.44,y’=0.07e^{2.88}< 0\)
Show that it is a maximum point
Question
The equation of a curve is \(x^3+3xy^2-y^3=5\).
(a) Show that \(\frac{dy}{dx}=\frac{x^2+y^2}{y^2-2xy}\).
(b) Find the coordinates of the points on the curve where the tangent is parallel to the y-axis.
Answer/Explanation
Ans:
(a) State or imply \(3y^2+6xy\frac{dy}{dx}\) as derivative of \(3xy^2\)
State or imply \(3y^2\frac{dy}{dx}\) as derivative of \(y^3\)
Equate attempted derivative of LHS to zero and solve for \(\frac{dy}{dx}\)
Obtain the given answer correctly
(b) Equate denominator to zero
Obtain y = 2x , or equivalent
Obtain an equation in x or y
Obtain the point (1,2)
State the point \((\sqrt[3]{5},0)\)
Question
The curve with equation y = xe1−2x has one stationary point.
(a)Find the coordinates of this point.
(b)Determine whether the stationary point is a maximum or a minimum.
Answer/Explanation
Ans:
(a)Use correct product rule
Obtain correct derivative in any form
Equate derivative to zero and solve for x
Obtain x = \(\frac{1}{2}\) and y = \(\frac{1}{2}\)
(b)
Use a correct method for determining the nature of a stationary point
Show that it is a maximum point
Question
The equation of a curve is \(y=x^{-\frac{2}{3}}\) ln x for x > 0. The curve has one stationary point.
(a) Find the exact coordinates of the stationary point. [5]
(b) Show that \(\int_{1}^{8}ydx=18ln2-9\) [5]
Answer/Explanation
Ans
(a) Use correct product rule or correct quotient rule
Obtain correct derivative in any form
Equate 2 term derivative to zero and solve for x
Obtain answer \(x=e^{\frac{3}{2}}\)
Obtain answer \(y=\frac{3}{2e}\
(b) Commence integration and reach \(ax^{\frac{1}{3}}ln\ x+b\int x^{\frac{1}{3}}\frac{1}{x}dx\)
Obtain \(3x^{\frac{1}{3}}ln \ x-3\int x^{\frac{1}{3}}\frac{1}{x}dx\)
Complete the integration and obtain \(3x^{\frac{1}{3}}ln \ x-9x^{\frac{1}{3}}\)
Use limits correctly in an expression of the form \(px^{\frac{1}{3}}ln\ x+qx^{\frac{1}{3}} (pq\neq 0)\)
Obtain 18ln 2 9 − from full and correct working
Question
The parametric equations of a curve are
\(x=ln(2+3t),\ y=\frac{t}{2+3t}\)
(a) Show that the gradient of the curve is always positive. [5]
(b) Find the equation of the tangent to the curve at the point where it intersects the y-axis. [3]
Answer/Explanation
Ans
(a) Use correct chain rule or correct quotient rule to differentiate x or y
Obtain \(\frac{dx}{dt}=\frac{3}{2+3t}\ or\ \frac{dy}{dt}=\frac{2}{(2+3t)^{2}}\)
Use \(\frac{dy}{dx}=\frac{dy}{dt}\div \frac{dx}{dt}\)
Obtain answer \(\frac{3}{3(2+3t)}\)
Explain why this is always positive
Alternative method for Question 6(a)
Form equation in x and y only
Obtain \(y=\frac{e^{x}-2}{3e^{2}}\left ( =\frac{1}{3}-\frac{2}{3}e^{-x} \right )\)
Differentiate
Obtain \(y’=\frac{2}{3}e^{-x}\)
Explain why this is always positive
(b) Obtain \(y=-\frac{1}{3}\ when\ x=0\)
Use a correct method to form the given tangent
Obtain answer 3y= 2x – 1
Question

The diagram shows the curve \(y=sin 2x cos^2\) for \(0≤x≤\frac{1}{2}\pi\), and its maximum point M.
(a) Using the substitution u = sin x, find the exact area of the region bounded by the curve and the x-axis.
(b) Find the exact x-coordinate of M.
Answer/Explanation
Ans:
- State or imply du =cos x dx
Using double angle formula for sin 2x and Pythagoras, express integral in terms of u and du.
Obtain integral \(\int 2(u-u^3)du\)
Use limits u = 0 and u = 1 in an integral of the form \(au^2+bu^4\), where ab≠0
Obtain answer \(\frac{a}{2}\) - Use product rule
Obtain correct derivative in any form
Equate derivative to zero and use a double angle formula
Obtain an equation in one trig variable
Obtain \(4x^2=1, 4cos^2x=3\) or \(3tan^2x=1\)
Obtain answer \(x=\frac{1}{6}\pi\)
Question
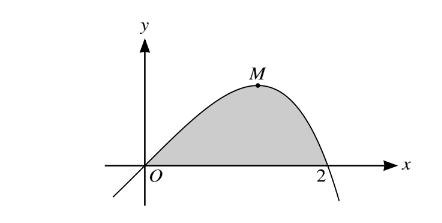
The diagram shows part of the curve\( y =(2x-x^{2})e^{\frac{1}{2}x}\) and its maximum point M.
(i) Find the exact x-coordinate of M.
(ii) Find the exact value of the area of the shaded region bounded by the curve and the positive x-axis
Answer/Explanation
.
(i) Use the correct product rule
Obtain correct derivative in any form, e.g.\( (2-2x)e^{\frac{1}{2}}+\frac{1}{2}(2x-x^{2})e^{\frac{1}{2}x}\)
Equate derivative to zero and solve for x
Obtain\( x \sqrt{5-1}\)
(ii) Integrate by parts and reach \(a(2x x^{2})e^{\frac{1}{2}x}+b\int (2-2x)e^{\frac{1}{2}x}dx\)
Obtain
\(2e^{\frac{1}{2}x}(2x-x^{2})-2\int (2-2x)e^{\frac{1}{2}x}\)
Complete the integration correctly, obtaining\( (12x-2x^{2}-24)e^{\frac{1}{2}}\)
Use limits x = 0, x = 2 correctly having integrated by parts twice
Obtain answer 24 – 8e, or exact simplified equivalent
Question
The equation of a curve is \(xy(x-6y)=9a^{3}\), where a is a non-zero constant. Show that there is only one point on the curve at which the tangent is parallel to the x-axis, and find the coordinates of this point.
Answer/Explanation
EITHER: EITHER: State(+x^{2}\frac{dy}{dx}\), or equivalent, as derivative of\( x^{2}y\)
State \( 6y^{2}+12xy\frac{dy}{dx}\),or equivalent, as derivative of\( 6xy^{2}\)
OR: Differentiating LHS using correct product rule, state term\( xy(1-6\frac{dy}{dx}) \)or equivalent
State term\( (y+x\frac{dy}{dx})(x-6y) \)or equivalent
Equate attempted derivative of LHS to zero and set \(\frac{dy}{dx}\)equal to zero
Obtain a horizontal equation, e.g.\( 6y^{2}-2xy=0 \)(from correct work only)
Explicitly reject y = 0 as a possibility \(py^{2}-qxy=0\)
Obtain an equation in x or y
Obtain answer (−3a, −a)
OR: Rearrange to -\(y=\frac{9a’}{x^{2}(x-6y)}\)
and use correct quotient rule to obtain -\(frac{9a’}{x^{2}(x-6y)} \)
State term \( (y+x\frac{dy}{dx})(x-6y) \)or equivalent
Justify division by x(x – 6y)
Set \( \frac{dy}{dx} \)equal to zero
Obtain a horizontal equation, e.g.\(6y^{2}-2xy =0\) (from correct work only)
Obtain an equation in x or y
Obtain answer (−3a, −a)
Question
The equation of a curve ia \(x^{3}-3x^{2}y+y^{3}=3\)
(i) Show that \(\frac{dy}{dx}=\frac{x^{2}-2xy}{x^{2}-y^{2}}\)
(ii) Find the coordinates of the points on the curve where the tangent is parallel to the x-axis
Answer/Explanation
.
(i) State or imply \(6xy+3x^{2}\frac{dy}{dx}\) as derivative of\( 3x^{2}y\)
State\( 3y^{2}\frac{dy}{dx}\)as derivative of\( y^{3}\)
Equate attempted derivative of the LHS to zero and solve \( for\frac{dy}{dx}\)
Obtain the given answer
(ii) Equate numerator to zero
Obtain x = 2y, or equivalent
Obtain an equation in x or y
Obtain the point (−2, −1)
State the point (0, 1.44)
Question
The curve with equation y = sin x cos 2x has one stationary point in the interval\( 0 < x <\frac{1}{2}\pi \) Find the
x-coordinate of this point, giving your answer correct to 3 significant figures
Answer/Explanation
.
Use product rule
Obtain correct derivative in any form, e.g. cosxcos2x-2sinxsin2x
Equate derivative to zero and use double angle formulae
Remove factor of cos x and reduce equation to one in a single trig function
Obtain \(6sin^{2}=1,6cos^{2}x=5 or 5tan^{2}x=1\)
Solve and obtain x = 0.421
[Alternative: Use double angle formula M1.Use chain rule to differentiate M1. Obtain correct
derivative
\(e.g.cos\Theta -6sin^{2}\Theta cos\Theta\) A1, then as above.]
Question
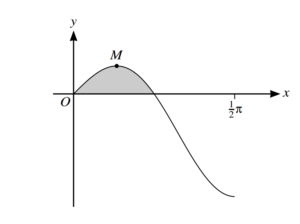
The diagram shows the curve y = sin x cos 2x for 0 ≤ x ≤ \(\frac{1}{2}\) π, and its maximum point M.
(a)Find the x-coordinate of M, giving your answer correct to 3 significant figures.
(b)Using the substitution u = cos x, find the area of the shaded region enclosed by the curve and the x-axis in the first quadrant, giving your answer in a simplified exact form.
Answer/Explanation
Ans:
(a)Use correct product rule or chain rule
Use correct product rule or chain rule
Equate derivative to zero and use a correct double angle formula
Obtain an equation in one trigonometric variable
Obtain 6sin2 x= 1, 6cos2 x= 5 or 5tan2 x=1
Obtain final answer x = 0.421
(b)
State or imply du =−sin x dx
Using double angle formula, express integral in terms of u and du
Integrate and obtain ± \(\left ( u – \frac{2}{3} u^{3}\right )\)
Use limits u = 1, u = \(\frac{1}{\sqrt{2}}\) in an integral of the form au + bu3 , where ab ≠ 0
Obtain \(\frac{1}{3}\left ( \sqrt{2} -1\right )or \frac{1}{3}\sqrt{2}\frac{1}{3} or \frac{2}{3}\left ( \frac{1}{\sqrt{2}} \right )\frac{1}{3}\) or simplified equivalent
Question
The parametric equations of a curve are
x = 1 – cos θ, \(y = cos\theta – \frac{1}{4}cos 2\theta \)
Show that \(\frac{dy}{dx} = -2sin^{2}\left ( \frac{1}{2}\theta \right )\) .
Answer/Explanation
Ans:
\(State \frac{dx}{d\theta } = sin \theta\) or \(\frac{dy}{d\theta } = -sin\theta +\frac{1}{2}sin2\theta \)
\(\frac{dy}{dx} = \frac{dy}{d\theta }\) ÷ \(\frac{dx}{d\theta}\)
Obtain correct answer in any form
Use double angle correctly to obtain \(\frac{dy}{dx}\) in terms of θ
Obtain the given answer with no errors seen− \(2sin^{2}\left ( \frac{1}{2}\theta \right )\)
Question
A curve has equation
sin y ln x = x − 2 sin y,
for – \(\frac{1}{2}\pi \leqslant y\leqslant \frac{1}{2}\pi \)
(i) Find \(\frac{dy}{dx}\) in terms of x and y. [5]
(ii) Hence find the exact x-coordinate of the point on the curve at which the tangent is parallel to the x-axis.[3]
Answer/Explanation
Ans:
6 (i) EITHER: State correct derivative of sin y with respect to x
Use product rule to differentiate the LHS
Obtain correct derivative of the LHS
Obtain a complete and correct derived equation in any form
Obtain a correct expression for \(\frac{dy}{dx}\) in any form
OR: State correct derivative of sin y with respect to x
Rearrange the given equation as sin y = x / (ln x + 2)and attempt to differentiate both sides
Use quotient or product rule to differentiate the RHS
Obtain correct derivative of the RHS
Obtain a correct expression for \(\frac{dy}{dx}\) in any form
(ii) Equate \(\frac{dy}{dx}\) to zero and obtain a horizontal equation in ln x or sin y
Solve for ln x
Obtain final answer x = 1/e , or exact equivalent
Question
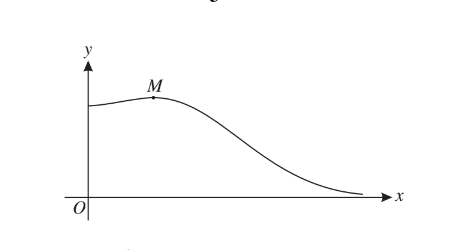
The diagram shows the curve y\(=e^{-\frac{1}{2}}\sqrt{(1+2x^{2})}\) for x ≥ 0, and its maximum point M.
(i) Find the exact value of the x-coordinate of M.
(ii) The sequence of values given by the iterative formula \(x_{n+1}=\sqrt{(In(4+8x^{2}_{n}))}\) with initial value \(x_{1}\) = 2, converges to a certain value α. State an equation satisfied by α and
hence show that α is the x-coordinate of a point on the curve where y = 0.5.
(iii) Use the iterative formula to determine α correct to 2 decimal places. Give the result of each
iteration to 4 decimal places.
Answer/Explanation
(i) Use correct product or quotient rule and use chain rule at least once Obtain derivative in any correct form Equate derivative to zero and solve an equation with at least two non-zero terms for real x
Obtain answer \( x=\frac{1}{\sqrt{2}}\),or exact equivalent
(ii) State a suitable equation, e.g. α =\(\sqrt{(In(4+8\alpha ^{2}))}\)
Rearrange to reach \(e^{a^{2}}=4+8a^{2}\)
Obtain\( \frac{1}{2}=e^{\frac{1}{2}^{a^{2}}}\sqrt{(1+2a^{2})}\) or work vice versa
(iii) Use the iterative formula correctly at least once Obtain final answer 1.86 Show sufficient iterations to 4 d.p. to justify 1.86 to 2 d.p., or show there is a sign change in the interval (1.855, 1.865)
Question
The equation of a curve is \(ln(xy) − y^{3}\) = 1.
(i) Show that\( x\frac{dy}{dx}\)=\(\frac{y}{x(3y^{3}-1)}\)
(ii) Find the coordinates of the point where the tangent to the curve is parallel to the y-axis, giving each coordinate correct to 3 significant figures.
Answer/Explanation
(i) EITHER: State or imply
\(\frac{1}{x}+\frac{1}{y}\frac{dy}{dx} y^{3}\) \(\frac{dy}{dx}\) as derivative of\( y^{3}\) , or equivalent
Equate derivative of LHS to zero and solve for\( frac{dy}{dx}\)
Obtain the given answer
[The is dependent on at least one of the B marks being earned]
(ii) Equate denominator to zero and solve for y
Obtain y = 0.693 only
Substitute found value in the equation and solve for x
Obtain x = 5.47 only
Question
The equation of a curve is \(3x^{2}-4xy+y^{2}=45\)
(i) Find the gradient of the curve at the point (2, −3).
(ii) Show that there are no points on the curve at which the gradient is 1.
Answer/Explanation
(i) Obtain\( 2y\frac{dy}{dx}\) as derivative of \( y^{2}\)
Obtain\( -4y-4x\frac{dy}{dx} as derivative of –4xy
Substitute x = 2 and y = –3 and find value of \(\frac{dy}{dx}\)
(dependent on at least one being earned and \(\frac{d(45)}{dx}=\)0)
Obtain \(\frac{12}{7}\) or equivalent
(ii) Substitute\( \frac{dy}\){dx} =1 in an expression involving\( \frac{dy}{dx} x\) and y and obtain ay = bx
Obtain y = x or equivalent
Uses y = x in original equation and demonstrate contradiction
Question
(i) By differentiating \(\frac{1}{cosx}\) , show that if y = sec x then\( \frac{dy}{dx}\) = sec x tan x.
(ii) Show that \(\frac{1}{(secx-tanx)}\) ≡ sec x + tan x.
(iii) Deduce that \(\frac{1}{(secx-tanx)^{2}}\) ≡ \(2 sec^{2}\)
x − 1 + 2 sec x tan x.
(iv) Hence show that \(\int_{0}^{\frac{1}{4}\pi }\frac{1}{(secx-tanx)^{2}}dx\)=\(\frac{1}{4}(8\sqrt{2}-\pi )\)
Answer/Explanation
(i) Use correct quotient or chain rule Obtain the given answer correctly having shown sufficient working
(ii) Use a valid method, e.g. multiply numerator and denominator by sec x + tan x, and a version of Pythagoras to justify the given identity
(iii) Substitute, expand
(sec x +\( tan x)^{2}\)
and use Pythagoras once
Obtain given identity
(iv) Obtain integral 2 tan x – x + 2 sec x
Use correct limits correctly in an expression of the form a tan x + bx + c sec x, or
equivalent, where abc 0
Obtain the given answer correctly
