Question
(i) By sketching a suitable pair of graphs, show that the equation\( x^{3}=3-x\)has exactly one real
root. [2]
(ii) Show that if a sequence of real values given by the iterative formula \(X_{n+1}=\frac{2x_{n}^{3}+3}{3x_{n}^{2}+1}\)
converges, then it converges to the root of the equation in part (i). [2]
(iii) Use this iterative formula to determine the root correct to 3 decimal places. Give the result of
each iteration to 5 decimal places. [3]
Answer/Explanation
3 (i) Sketch a relevant graph, e.g.y=\(x^{3}\)
Sketch a second relevant graph, e.g. y = 3 –x, and justify the given statement
3(ii) State or imply the equation\( x (2x^{3}++3)/(3x^{2}+1)\)
Rearrange this in the form \(x^{3}=3-x\) or commence work vice versa
3(iii) Use the iterative formula correctly at least once Obtain final answer 1.213
Show sufficient iterations to 5 d.p. or more to justify 1.213 to 3 d.p., or show there is a
sign change in the interval (1.2125, 1.2135)
Question
The sequence of values given by the iterative formula
\(X_{n+1}=\frac{2{x_{n}}^{6}+12x_{n}}{3x_{n}^{5}+8}\)
with initial value\( x_{1}\) = \(2, converges to \alpha\)
(i) Use the formula to calculate ! correct to 4 decimal places. Give the result of each iteration to
6 decimal places.
(ii) State an equation satisfied by ! and hence find the exact value of \(\alpha \)
Answer/Explanation
(i) Use the iterative formula correctly at least once
Obtain answer 1.3195
Show sufficient iterations to 6 d.p. to justify 1.3195 to 4 d.p., or show there is a sign change in (1.31945, 1.31955)
(ii) State x = \(\frac{2x^{6}+12x}{3x^{5}+8}\) , or equivalent
State answer\( \sqrt[5]{4}\)
Question
The curve with equation\( y = =e^{-2x}In (x-1)\) has a stationary point when x = p.
(i) Show that p satisfies the equation x =\( 1 + exp\left ( \frac{1}{2(x-1)} \right )\),\ , where exp(x )denotes \(e^{x}\)
(ii) Verify by calculation that p lies between 2.2 and 2.6.
(iii) Use an iterative formula based on the equation in part (i) to determine p correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i) Use correct product rule Obtain correct derivative in any form\( \frac{dy}{dx}= -2e^{-2x}In (x-1)+\frac{e^{-2x}}{x-1}\) Equate derivative to zero and derive\( x=1+e^{\frac{1}{2(x+1)}} or p= 1+\frac{1}{2(p-1)}\)
(ii) Calculate values of a relevant expression or pair of relevant expressions at x = 2.2 and x = 2.6
\(f(x)= In (x-1)-\frac{1}{2(x-1)}\Rightarrow f(2.2)=-0.2334,f(2.6)=0.317\)
\(f(x)=2e^{-2x} In (x-1)+\frac{e^{-2x}}{x-1}\Rightarrow f(2.2)=0.005…ff(2.6)=-0.0017..\) Complete the argument correctly with correct calculated values
(iii) Use the iterative process \( p_{n+1}=1+exp\left ( \frac{1}{2(p_{n-1})} \right )\) correctly at least once Obtain final answer 2.42
Show sufficient iterations to 4 d.p. to justify 2.42 to 2 d.p., or show there is a sign
change in the interval (2.415, 2.425)
Question
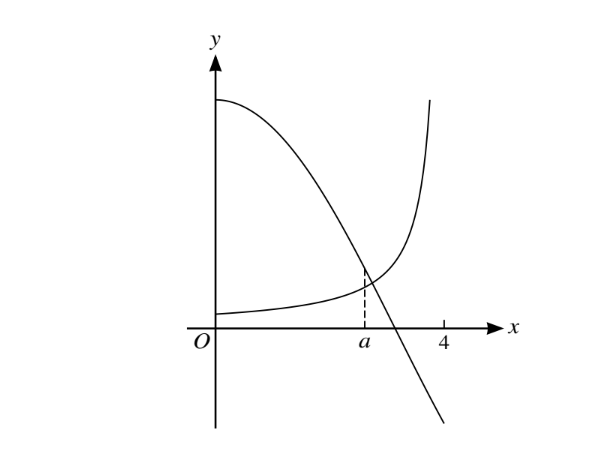
The diagram shows the curves y =\(4cos\frac{1}{2}xand y=\frac{1}{4-x,}\) for 0 ≤ x < 4. When x = a, the tangents to the curves are perpendicular.
(i) Show that a =\(4-\sqrt{(2sin\frac{1}{2}a)}\)
(ii) Verify by calculation that a lies between 2 and 3.
(iii) Use an iterative formula based on the equation in part (i) to determine a correct to 3 decimal places. Give the result of each iteration to 5 decimal places.
Answer/Explanation

Question
The sequence of values given by the iterative formula \(x_{n+1}=\frac{2x^{6}_{n}+12x_{n}}{3x_{n}^{5}+8},\)with initial value 2, converges to
(i) Use the formula to calculate ! correct to 4 decimal places. Give the result of each iteration to
6 decimal places.
(ii) State an equation satisfied by ! and hence find the exact value of \alpha
Answer/Explanation
(i) Use the iterative formula correctly at least once Obtain answer 1.3195
Show sufficient iterations to 6 d.p. to justify( 1.3195 to 4 d.p., or show there is a sign change in (1.31945, 1.31955)
(ii) State \(x=\frac{2x^{6}+12x}{3x^{5}+8}\), or equivalent State answer \(\sqrt[5]{4}\), or exact equivalent
Question
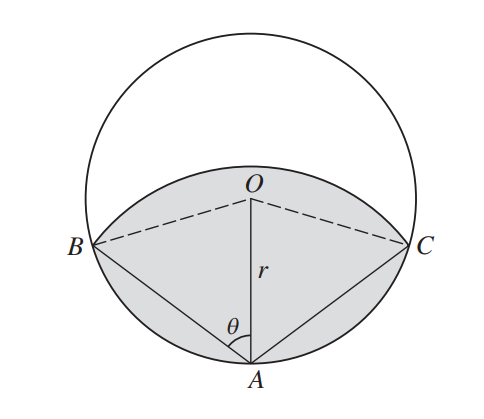
In the diagram, A is a point on the circumference of a circle with centre O and radius r. A circular arc with centre A meets the circumference at B and C. The angle OAB is θ radians. The shaded region is bounded by the circumference of the circle and the arc with centre A joining B and C. The area of the shaded region is equal to half the area of the circle.
(i) Show that \(cos2\theta =\frac{2sin2\theta -\pi }{4\theta}\). [5]
(ii) Use the iterative formula \(\theta _{n+1}=\frac{1}{2}cos^{-1}\left ( \frac{2sin2\theta_{n}-\pi}{4\theta_{n}} \right ),\)
with initial value θ1= 1, to determine θ correct to 2 decimal places, showing the result of each iteration to 4 decimal places. [3]
Answer/Explanation
Ans:
(i) State or imply AB = 2r cosθ or AB2 = 2r2 – 2r2 cos(π-2θ)
Use correct formula to express the area of sector ABC in terms of r and θ
Use correct area formulae to express the area of a segment in terms of r and θ
State a correct equation in r and θ in any form
Obtain the given answer
[SR: If the complete equation is approached by adding two sectors to the shaded area above BO and OC give the first M1 as on the scheme, and the second M1 for using correct area formulae for a triangle AOB or AOC, and a sector AOB or AOC.]
(ii) Use the iterative formula correctly at least once
Obtain final answer 0.95
Show sufficient iterations to 4 d.p. to justify 0.95 to 2 d.p., or show there is a sign change in the interval (0.945, 0.955)
Question
Liquid is flowing into a small tank which has a leak. Initially the tank is empty and, t minutes later, the volume of liquid in the tank is V cm3. The liquid is flowing into the tank at a constant rate of 80 cm3 per minute. Because of the leak, liquid is being lost from the tank at a rate which, at any instant, is equal to kV cm3 per minute where k is a positive constant.
(i) Write down a differential equation describing this situation and solve it to show that [7]
\(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\)
(ii) It is observed that V = 500 when t = 15, so that k satisfies the equation
\(k=\frac{4-4e^{-kt} }{25}\)
Use an iterative formula, based on this equation, to find the value of k correct to 2 significant figures. Use an initial value of k = 0.1 and show the result of each iteration to 4 significant figures. [3]
(iii) Determine how much liquid there is in the tank 20 minutes after the liquid started flowing, and state what happens to the volume of liquid in the tank after a long time.[2]
Answer/Explanation
Ans:
(i) State \(\frac{dV}{dt}=80-kV\)
Correctly separate variables and attempt integration of one side
Obtain a ln(80 − kV) = t or equivalent
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t\) or equivalent
Use t = 0 and V = 0 to find constant of integration or as limits
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t-\frac{1}{k}\) or equivalent
Obtain given answer \(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\) correctly
(ii) Use iterative formula correctly at least once
Obtain final answer 0.14
Show sufficient iterations to 4 s.f. to justify answer to 2 s.f. or show a sign change in the interval (0.135, 0.145)
(iii) State a value between 530 and 540 cm3 inclusive
State or imply that volume approaches 569 cm3 (allowing any value between 567 and 571 inclusive)
Question
The equation \(x^{3}\) = 3x + 7 has one real root, denoted by \(\alpha\)
(i) Show by calculation that ! lies between 2 and 3.
Two iterative formulae, A and B, derived from this equation are as follows:
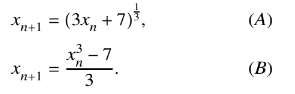
Each formula is used with initial value \(x_{1} = 2.5\).
(ii) Show that one of these formulae produces a sequence which fails to converge, and use the other
formula to calculate ! correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
3(i) Calculate value of a relevant expression or expressions at x = 2 and x = 3
Complete the argument correctly with correct calculated values 2
3(ii) Use an iterative formula correctly at least once
Show that (B) fails to converge
Using (A), obtain final answer 2.43
Show sufficient iterations to justify 2.43 to 2 d.p., or show there is a sign change in
(2.425, 2.435)
Question
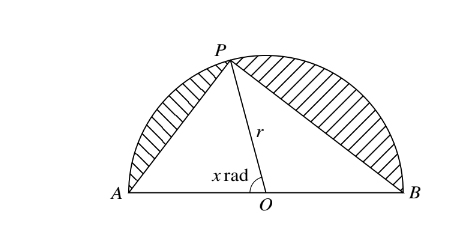
The diagram shows a semicircle with centre O, radius r and diameter AB. The point P on its
circumference is such that the area of the minor segment on AP is equal to half the area of the minor
segment on BP. The angle AOP is x radians.
(i) Show that x satisfies the equation \(x=\frac{1}{3}(\pi +sinx)\).
(ii) Verify by calculation that x lies between 1 and 1.5.
(iii) Use an iterative formula based on the equation in part (i) to determine x correct to 3 decimal
places. Give the result of each iteration to 5 decimal places.
Answer/Explanation
5(i) Use correct sector formula at least once and form an equation in r and x Obtain a correct equation in any form
Rearrange in the given form
Total: 3
5(ii) Calculate values of a relevant expression or expressions at x = 1 and x = 1.5
Complete the argument correctly with correct calculated values
(iii) Use the iterative formula correctly at least once
Obtain final answer 1.374
Show sufficient iterations to 5 d.p. to justify 1.374 to 3 d.p., or show there is a sign
change in the interval (1.3745, 1.3755)
Question
(i) By sketching suitable graphs, show that the equation \(e^-{\frac{1}{2}x}=4-x^{2}\) has one positive root and one negative root.
(ii) Verify by calculation that the negative root lies between −1 and −1.5.
(iii) Use the iterative formula \( x_{n+1}=-\sqrt{4-e^-{\frac{1}{2}x_{n}}}\)to determine this root correct to 2 decimal places.
Give the result of each iteration to 4 decimal places.
Answer/Explanation
(i) Sketch a relevant graph, e.g.\(y=e^-{\frac{1}{2}x}\)
Sketch a second relevant graph, e.g.\( y=4-x^{2}\)and justify the given statement
(ii) Calculate the value of a relevant expression or values of a pair of expressions at x = – 1 and x = – 1.5
complete the argument correctly with correct calculated values
(iii) Use the iterative formula correctly at least once
Obtain final answer – 1.41
Show sufficient iterations to 4 d.p. to justify – 1.41 to 2 d.p., or show there is a sign
change in the interval ( – 1.415, – 1.405)
Question
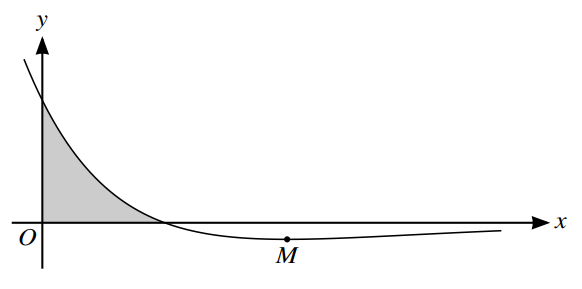
The diagram shows the curve \(7=(2-x)e^{-\frac{1}{2}x}\), and its minimum point M.
(a) Find the exact coordinates of M. [5]
(b) Find the area of the shaded region bounded by the curve and the axes. Give your answer in terms
of e. [5]
Answer/Explanation
(a) Use correct product or quotient rule
Obtain correct derivative in any form
Equate derivative to zero and solve for x D
Obtain x = 4 A1 ISW
Obtain y = –2e–2, or exact equivalent
(b) Commence integration and reach
\(a(2-x)e^{-\frac{1}{2}x}+b\int e^{-\frac{1}{2}x}dx\)
Obtain \(-2(2-x)e^{-\frac{1}{2}x}-2\int e^{-\frac{1}{2}x}dx\)
Complete integration and obtain \(2xe^{-\frac{1}{2}x}\)
Use correct limits, x = 0 and x = 2, correctly, having integrated
twice
Obtain answer 4e–1, or exact equivalent
Alternative method for question (b)
\(\frac{d\left ( 2xe^{-\frac{1}{2}x} \right )}{dx}=2e^{-\frac{1}{2}x}-xe^{-\frac{1}{2}x}\)
∴\(2xe^{-\frac{1}{2}x}\)
Use correct limits, x = 0 and x = 2, correctly, having integrated
twice
Obtain answer 4e–1, or exact equivalent
Question
(a) By sketching a suitable pair of graphs, show that the equation cosec \( x=1+e^{-\frac{1}{2}x}\) has exactly two
roots in the interval 0 < x < π. [2]
(b) The sequence of values given by the iterative formula
\(x_{n+1}=\pi -\sin ^{-1}\left ( \frac{1}{e^{-\frac{1}{2}x_{n}+1}} \right )\)
with initial value x1 = 2, converges to one of these roots.
Use the formula to determine this root correct to 2 decimal places. Give the result of each
iteration to 4 decimal places. [3]
Answer/Explanation
Ans
(a) Sketch a relevant graph, e.g. y = cosec x
Sketch a second relevant graph, e.g \(y=1+e^{-\frac{1}{2}x}\), and justify the
given statement
(b) Use the iterative formula correctly at least twice
Obtain final answer 2.28
Show sufficient iterations to at least 4 d.p. to justify 2.28 to
2 d.p., or show there is a sign change in the interval (2.275,
2.285)
Question
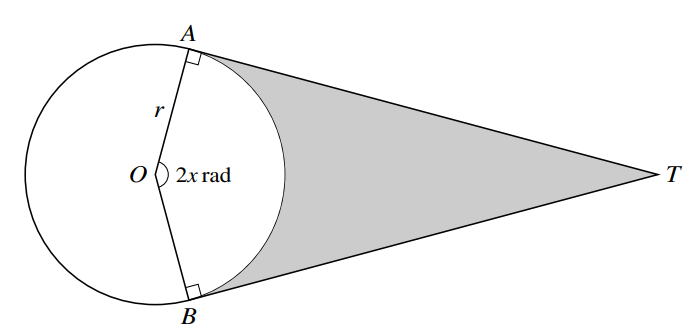
The diagram shows a circle with centre O and radius r. The tangents to the circle at the points A and
B meet at T, and angle AOB is 2x radians. The shaded region is bounded by the tangents AT and BT,
and by the minor arc AB. The area of the shaded region is equal to the area of the circle.
(a) Show that x satisfies the equation tan x = π + x. [3]
(b) This equation has one root in the interval \(0< x< \frac{1}{2}\pi \). Verify by calculation that this root lies
between 1 and 1.4. [2]
(c) Use the iterative formula
\(x_{n+1}=\tan ^{-1}(\pi +x_{n})\)
to determine the root correct to 2 decimal places. Give the result of each iteration to 4 decimal
places. [3]
Answer/Explanation
Ans
(a) State or imply AT = r tan x or BT = r tan x
Use correct area formula and form an equation in r and x
Rearrange in the given form
(b) Calculate the values of a relevant expression or pair of expressions at x = 1 and x = 1.4
Complete the argument correctly with correct calculated values
(c) Use the iterative formula correctly at least once
Obtain final answer 1.35
Show sufficient iterations to 4 d.p. to justify 1.35 to 2 d.p. or show there is a sign change in the interval (1.345, 1.355)
Question
(a) By sketching a suitable pair of graphs, show that the equation sec x = 2 – \(\frac{1}{2}\)x has exactly one root in the interval \(0\leq x < \frac{1}{2} \pi\).
(b) Verify by calculation that this lies between 0.8 and 1
(c) Use the iterative formula \(x_{n+1}=cos^{-1}(\frac{2}{4-x_n})\) to determine the root correct to 2 decimal places.
Give the result of each iteration to 4 decimal places.
Answer/Explanation
Ans:
(a) Sketch the graph y = sec x
Sketch the graph \(y=2-\frac{1}{2}\), and justify the given statement
(b) Calculate the values of a relavant expression or pair of expressions at x = 0.8 and x = 1
Complete the argument correctly with correct calculated values
(c) Use the iterative formula correctly at least once
Obtain final answer 0.88
Show sufficient iteratives to 4 d.p. to justify 0.88 to 2 d.p., or show there is a sign change in the interval (0.875, 0.885)
The constant a is such that \(\int_{1}^{a}\frac{ln x}{\sqrt{x}}dx = 6.\)
(a) Question
Show that a = exp \(\left ( \frac{1}{\sqrt{a}} +2\right )\)[exp (x) is an alternative notation for ex.]
(b) Question
Verify by calculation that a lies between 9 and 11.
(c) Question
Use an iterative formula based on the equation in part (a) to determine a correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
Ans:(a)
Commence integration and reach \(a\sqrt{x} ln x + b \int \sqrt{x}. \frac{1}{x} dx, or equivalent\)
Obtain \(2\sqrt{x} ln x -\int 2\sqrt{x}. \frac{1}{x} dx, or equivalent\)
Obtain integral \(2\sqrt{x} ln x -4\sqrt{x}, or equivalent\)
Substitute limits and equate result to 6
Rearrange and obtain a = exp \(\left ( \frac{1}{\sqrt{a}} + 2\right )\)
Ans:(b)
Calculate the values of a relevant expression or pair of expressions at a = 9 and a = 11
Complete the argument correctly with correct values
Ans:(c)
Use the iterative process an+1 = exp\(\left ( \frac{1}{\sqrt{a_{n}}} + 2 \right )\) correctly at least once
Obtain answer 10.12
Show sufficient iterations to 4dp to justify 10.12 to 2dp, or show there is a sign change in the interval (10.115, 10.125)
Question
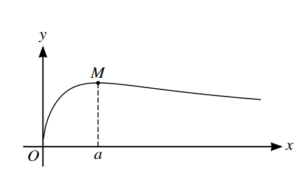
The diagram shows the curve \(y=\frac{\tan ^{-1}x}{\sqrt{x}}\)
(a) Show that a satisfies the equation
\(a=\tan \left ( \frac{2a}{1+a^{2}} \right )\) [4]
(b) Verify by calculation that a lies between l.3 and 1.5. [2]
(c) Use an iterative formula based on the equation in part (a) to determine a correct to 2 decimal
places. Give the result of each iteration to 4 decimal places. [3]
Answer/Explanation
Ans
(a) Use correct quotient rule or correct product rule
Obtain correct derivative in any form
Equate derivative to zero and remove inverse tangent
Obtain \(a=\tan \left ( \frac{2a}{1+a^{2}} \right )\) from correct working
(b) Calculate the value of a relevant expression or pair of expressions at a = 1.3 and a = 1.5
Complete the argument correctly with correct calculated values
(c) Use the iterative process \(a_{n+1}=\tan \left ( \frac{2a_{n}}{1+a_{n}^{2}} \right )\) correctly at least twice
Obtain final answer 1.39
Show sufficient iterations to at least 4 d.p. to justify 1.39 to 2 d.p. or show
there is a sign change in the interval (1.385, 1.395)
Question
Find the real root of the equation \(\frac{2e^{x}+e^{-x}}{2+e^{x}}=3\), giving your answer correct to 3 decimal places.
Your working should show clearly that the equation has only one real root. [5]
Answer/Explanation
Ans
2 Reduce to a 3-term quadratic u2 + 6u −1= 0 OE
Solve a 3-term quadratic for u
Obtain root \(\sqrt{10}-3\)
Obtain answer x = – 1.818 only
Reject \(-\sqrt{10}-3\) correctly
Alternative method for Question 2
Rearrange to obtain a correct iterative formula
Use the iterative process at least twice
Obtain answer x = – 1.818
Show sufficient iterations to at least 4 d.p. to justify x = – 1.818
Clear explanation of why there is only one real root
Question
Let f(x)=\(\frac{e^{2x}+1}{e^{2x}-1}\), for x>0.
(a) The equation x=f(x) has one root, denoted by a.Verify by calculation that a lies between 1 and 1.5
(b) Use an iterative formula based on the equation in part (a) to determine a correct to 2 decimal places. Give the result of each iteration to 4 decimal place.
(c) Find f'(x). Hence find the exact value of x for which f'(x)=-8.
Answer/Explanation
Ans:
- Calculate the values of a relevant expression or pair of expression at x=1 and x=1.5
Complete the argument correctly with correct calculated values - Use the iterative formula \(x_{n+1}=\frac{e^{2x_n}+1}{e^{2x_n}-1}\), or equivalent, correctly at least once
Obtain final answer 1.20
Show sufficient iterations to 4dp to justify 1.20 to 2 dp, show there is a sign change in the interval(1.195, 1.205) - Use quotient rule
Obtain correct derivative in any form
Equate derivative to -8 and obtain a quadratic in \(e^{2x}\)
Obtain \(2(e^{2x})^2-5e^{2x}+2=0\)
Solve a 3-term quadratic in \(e^{2x}\) for x
Obtain answer \(x=\frac{1}{2} In 2\), or exact equivalent, only
Alternative method for question 9(c)
Use quotient rule
Obtain correct derivative in any form
Equate derivative to -8, take square roots and obtain a quadratic in \(e^x\)
Obtain \(\sqrt{2e^{2x}}-e^x-\sqrt{2}=0\)
Solve a 3-term quadratic in \(e^x\) for x
Obtain answer \(x=\frac{1}{2}In2\), or exact equivalent, only
Question
Let f(x)=\(\frac{e^{2x}+1}{e^{2x}-1}\), for x>0.
(a) The equation x=f(x) has one root, denoted by a.
Verify by calculation that a lies between 1 and 1.5
(b) Use an iterative formula based on the equation in part (a) to determine a correct to 2 decimal places. Give the result of each iteration to 4 decimal place.
(c) Find f'(x). Hence find the exact value of x for which f'(x)=-8.
Answer/Explanation
Ans:
- Calculate the values of a relevant expression or pair of expression at x=1 and x=1.5
Complete the argument correctly with correct calculated values - Use the iterative formula \(x_{n+1}=\frac{e^{2x_n}+1}{e^{2x_n}-1}\), or equivalent, correctly at least once
Obtain final answer 1.20
Show sufficient iterations to 4dp to justify 1.20 to 2 dp, show there is a sign change in the interval(1.195, 1.205) - Use quotient rule
Obtain correct derivative in any form
Equate derivative to -8 and obtain a quadratic in \(e^{2x}\)
Obtain \(2(e^{2x})^2-5e^{2x}+2=0\)
Solve a 3-term quadratic in \(e^{2x}\) for x
Obtain answer \(x=\frac{1}{2} In 2\), or exact equivalent, only
Alternative method for question 9(c)
Use quotient rule
Obtain correct derivative in any form
Equate derivative to -8, take square roots and obtain a quadratic in \(e^x\)
Obtain \(\sqrt{2e^{2x}}-e^x-\sqrt{2}=0\)
Solve a 3-term quadratic in \(e^x\) for x
Obtain answer \(x=\frac{1}{2}In2\), or exact equivalent, only
Question
(i) By sketching a suitable pair of graphs, show that the equation \(cosec\frac{1}{2}x=\frac{1}{3}x+1\) has one root in the interval 0 < x ≤ π.
(ii) Show by calculation that this root lies between 1.4 and 1.6.
(iii) Show that, if a sequence of values in the interval 0 < x ≤ π given by the iterative formula\(x_{n+1}=2sin^{-1}(\frac{3}{x_{n}+3})\) converges, then it converges to the root of the equation in part (i).
(iv) Use this iterative formula to calculate the root correct to 3 decimal places. Give the result of each
iteration to 5 decimal places
Answer/Explanation
.
(i) Make recognizable sketch of a relevant graph
Sketch the other relevant graph and justify the given statement
(ii) Use calculations to consider the value of a relevant expression at x = 1.4 and x = 1.6, or the values of relevant expressions at x = 1.4 and x = 1.6 Complete the argument correctly with correct calculated values
(iii) State\( x=2sin^{-1}\left ( \frac{3}{x+3} \right )\)
Rearrange this in the form \(cosec\frac{1}{2}x=\frac{1}{3}x+1\)
If working in reverse, need \(sin\frac{x}{2}=\left ( \frac{3}{x+3} \right )\)
(iv) Use the iterative formula correctly at least once
Obtain final answer 1.471
Show sufficient iterations to 5 d.p. to justify 1.471 to 3 d.p., or show there is a sign
change in the interval (1.4705, 1.4715)
Question
(i) By sketching a suitable pair of graphs, show that the equation
\(5e^{-x}=\sqrt{x}\)
has one root.
(ii) Show that, if a sequence of values given by the iterative formula
\(x_{n+1}=\frac{1}{2}In (\frac{25}{x_{n}})\)
converges, then it converges to the root of the equation in part (i).
(iii) Use this iterative formula, with initial value \(x_{1}=1\) to calculate the root correct to 2 decimal
places. Give the result of each iteration to 4 decimal places.
Answer/Explanation
[3]
(i) Make recognizable sketch of a relevant graph Sketch the other relevant graph and justify the given statement
(ii) State\( x=\frac{1}{2}In(25/x)\)
Rearrange this in the form \(5e^{-x}=\sqrt{x}\)
(iii) Use the iterative formula correctly at least once Obtain final answer 1.43 Show sufficient iterations to 4 d.p. to justify 1.43 to 2 d.p., or show there is a sign change in the interval (1.425, 1.435)
Question
(a) By sketching a suitable pair of graphs, show that the equation 4 − x 2 = sec \(\frac{1}{2}x\) has exactly one root in the interval 0 ≤ x < π.
(b)Verify by calculation that this root lies between 1 and 2.
(c)Use the iterative formula \(x_{n+1} = \sqrt{4-sec\frac{1}{2}x_{n}}\) to determine the root correct to 2 decimal places.
Give the result of each iteration to 4 decimal places.
Answer/Explanation
Ans:
(a)Sketch a relevant graph, e.g. y = 4 – x2
Sketch a second relevant graph, e.g. y = sec \(\frac{1}{2}x\) , and justify the give statement
(b)Calculate the value of a relevant expression or values of a pair of relevant expressions at x = 1 and x = 2
Complete the argument with correct calculated values
(c)
Use the iterative process correctly at least twice
Obtain final answer 1.60
Show sufficient iterations to 4 d.p.to justify 1.60 to 2 d.p. or show there is a sign change in the interval (1.595, 1.605)
f
Question
The equation x5 − 3x3 + x2 − 4 = 0 has one positive root.
(i) Verify by calculation that this root lies between 1 and 2. [2]
(ii) Show that the equation can be rearranged in the form [1]
\(x=\sqrt[3]{\left ( 3x+\frac{4}{x^{2}} -1\right )}\)
(iii) Use an iterative formula based on this rearrangement to determine the positive root correct to 2 decimal places. Give the result of each iteration to 4 decimal places.[3]
Answer/Explanation
Ans:
3 (i) Consider sign of x5 − 3x3 + x2 − 4 at x = 1 and x = 2 , or equivalent
Complete the argument correctly with correct calculated values
(ii) Rearrange the given quintic equation in the given form, or work vice versa
(iii) Use the iterative formula correctly at least once
Obtain final answer 1.78
Show sufficient iterations to 4 d.p. to justify 1.78 to 2 d.p., or show there is a sign change in the interval (1.775, 1.785)
Question
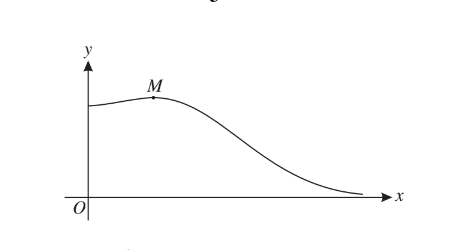
The diagram shows the curve y\(=e^{-\frac{1}{2}}\sqrt{(1+2x^{2})}\) for x ≥ 0, and its maximum point M.
(i) Find the exact value of the x-coordinate of M.
(ii) The sequence of values given by the iterative formula \(x_{n+1}=\sqrt{(In(4+8x^{2}_{n}))}\) with initial value \(x_{1}\) = 2, converges to a certain value α. State an equation satisfied by α and
hence show that α is the x-coordinate of a point on the curve where y = 0.5.
(iii) Use the iterative formula to determine α correct to 2 decimal places. Give the result of each
iteration to 4 decimal places.
Answer/Explanation
(i) Use correct product or quotient rule and use chain rule at least once Obtain derivative in any correct form Equate derivative to zero and solve an equation with at least two non-zero terms for real x
Obtain answer \( x=\frac{1}{\sqrt{2}}\),or exact equivalent
(ii) State a suitable equation, e.g. α =\(\sqrt{(In(4+8\alpha ^{2}))}\)
Rearrange to reach \(e^{a^{2}}=4+8a^{2}\)
Obtain\( \frac{1}{2}=e^{\frac{1}{2}^{a^{2}}}\sqrt{(1+2a^{2})}\) or work vice versa
(iii) Use the iterative formula correctly at least once Obtain final answer 1.86 Show sufficient iterations to 4 d.p. to justify 1.86 to 2 d.p., or show there is a sign change in the interval (1.855, 1.865)
Question
Solve the equation
\(5^{x−1} \)=\( 5^{x }− 5\),
giving your answer correct to 3 significant figures.
Answer/Explanation
EITHER Use laws of indices correctly and solve for 5^{x} or for \( 5^{–x}\)
or for \(5^{x–1}\)
Obtain\( 5^{x}\)
or for\( 5^{–x}\)
or for\( 5 ^{x–1}\)
in any correct form, e.g. \(5^{x}\)\( \frac{5}{1-\frac{1}{5}}\)
Use correct method for solving \(5^{x}\) = a, or \(5^{–x} \) = a, or \(5^{x–1}\) = a, where a 0 Obtain answer x = 1.14
OR Use an appropriate iterative formula, \(x_{n+1}\)=\(\frac{In(5^{x-1+5})} {In5} \)correctly, at least once
Obtain answer 1.14
Obtain answer 1.14
Show sufficient iterations to at least 3 d.p. to justify 1.14 to 2 d.p., or show there is a sign change in the interval (1.135, 1.145) Show there is no other root [For the solution x = 1.14 with no relevant working give , and a further B1 if
1.14 is shown to be the only solution.]
Question
(i) It is given that 2 tan 2x + \(5{tan^{2}x\) = 0. Denoting tan x by t, form an equation in t and hence show that either t = 0 or t = \(\sqrt[3](t+0.8)\).
(ii) It is given that there is exactly one real value of t satisfying the equation t =
√3(t + 0.8). Verify by calculation that this value lies between 1.2 and 1.3.
(iii) Use the iterative formula t _{n}+1=√3(t_{n}_+ 0.8) \)to find the value of t correct to 3 decimal places. Give the result of each iteration to 5 decimal places.
(iv) Using the values of t found in previous parts of the question, solve the equation 2 tan 2x + 5 \(tan^{2} x \)= 0 for −π ≤ x ≤ π.
Answer/Explanation
(i) Use correct identity for tan 2x and obtains at \(4 + bt^{3}+ ct^{2}+ dt\) = 0, where b may be zero
Obtain correct horizontal equation, e.g. 4t +\( 5t^{2}– 5t^{4} \)= 0
Obtain \(kt(t^{3}+ et + f)\) = 0 or equivalent
Confirm given results t = 0 and 3 t = t + 0.8
(ii) Consider sign of 3 t − t + 0.8 at 1.2 and 1.3 or equivalent
Justify the given statement with correct calculations (–0.06 and 0.02)
(iii) Use the iterative formula correctly at least once with\( 1.2 < t_{n} < 1.3 \)
Obtain final answer 1.276
Show sufficient iterations to justify answer or show there is a change of sign in interval
(1.2755, 1.2765)
(iv) Evaluate\( tan^{–1}\) (answer from part (iii)) to obtain at least one value
Obtain –2.24 and 0.906
State –π, 0 and π
[SR If A0, B0, allow B1 for any 3 roots]