Qurstion
The straight line l has equation r = 4i − j + 2k + , \(\lambda (2i− 3j + 6k)\). The plane p passes through the point( 4, −1, 2 )and is perpendicular to l.
(i) Find the equation of p, giving your answer in the form ax + by + cÏ = d.
(ii) Find the perpendicular distance from the origin to p.
(iii) A second plane q is parallel to p and the perpendicular distance between p and q is 14 units.
Find the possible equations of q.
Answer/Explanation
(i)
(i) Obtain 2x – 3y + 6z for LHS of equation
Obtain 2x – 3y + 6z = 23
(ii) Either Use correct formula to find perpendicular distance
Obtain unsimplified value \(frac{\pm 23}{\sqrt{2^{2}+(-3)^{2}+6^{2}}}\), following answer to (i)
Obtain \(\frac{23}{7}\)or equivalent
OR 1 Use scalar product of (4, –1, 2) and a vector normal to the plane
Use unit normal to plane to obtain\( \pm\frac{(8+3+12){\sqrt{49}}\)
Obtain distance\( \frac{23}{7}\) or equivalent
OR 2 Find parameter intersection of p and \(r=\mu (2i-3j+6k)\)
Obtain \(\mu =\frac{23}{49 }[and\left ( \frac{46}{49},-\frac{69}{49},\frac{138}{49} \right )\)as foot of perpendicular]
Obtain distance \(\frac{23}{7}\) or equivalent
(iii) Either Recognise that plane is 2x – 3y + 6z = k and attempt use of formula for
perpendicular distance to plane at least once
Obtain\( \frac{|23-k|}{7}=14 \) or equivalent
Obtain 2x – 3y + 6z = 121 and 2x – 3y + 6z = –75
OR Recognise that plane is 2x – 3y + 6z = k and attempt to find at least one
point on q using l with λ = ±2
Obtain 2x – 3y + 6z = 121
Obtain 2x – 3y + 6z = –75
Question
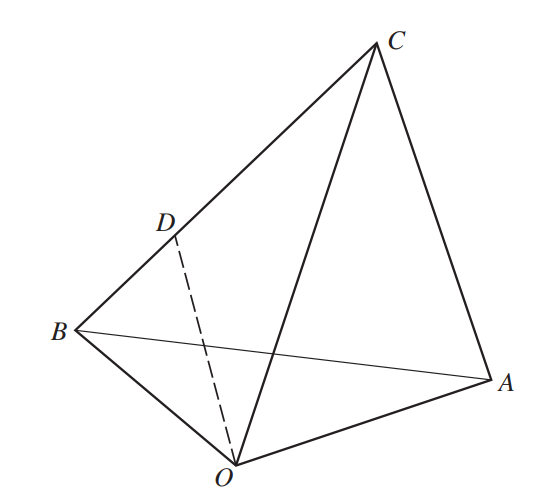
The diagram shows three points A, B and C whose position vectors with respect to the origin O are given by \(\underset{OA}{\rightarrow}=\begin{pmatrix}2\\-1\\2\\\end{pmatrix}, \underset{OB}{\rightarrow}=\begin{pmatrix}0\\3\\1\\\end{pmatrix}\) and \(\underset{OC}{\rightarrow}=\begin{pmatrix}3\\0\\4\\\end{pmatrix}\). The point D lies on BC, between B and C, and is such that CD = 2DB.
(i) Find the equation of the plane ABC, giving your answer in the form ax + by + cz = d. [6]
(ii) Find the position vector of D. [1]
(iii) Show that the length of the perpendicular from A to OD is \(\frac{1}{3}\sqrt{\left ( 65 \right )}\).[4]
Answer/Explanation
Ans:


Question
With respect to the origin O, the vertices of a triangle ABC have position vectors
\(\overrightarrow{OA}=2i+5k,\ \overrightarrow{OB}=3i+2j+3k\ and \ \overrightarrow{OC}=i+j+k\)
(a) Using a scalar product, show that angle ABC is a right angle. [3]
(b) Show that triangle ABC is isosceles. [2]
(c) Find the exact length of the perpendicular from O to the line through B and C. [4]
Answer/Explanation
Ans
(a) State \(\overrightarrow{AB}(or\ \overrightarrow{BA})\ and \ \overrightarrow{BC}(or \ \overrightarrow{CB})\ in \ vector \ form\)
Calculate their scalar product
Show product is zero and confirm angle ABC is a right angle
(b) Use correct method to calculate the lengths of AB and BC
Show that AB = BC and the triangle is isosceles
(c) State a correct equation for the line through B and C,
e.g. r = i + j + k + λ (2i + j + 2k) or 3i+ 2j + 3k + μ (-21 – j – 2k)
Taking a general point of BC to be P, form an equation in λ by either equating the scalar product of \(\overrightarrow{OP}\ and \ \overrightarrow{BC}\) to zero,
or applying Pythagoras to triangle OBP (or OCP), or setting the derivative of \(|\overrightarrow{OP}|\) to zero
Solve and obtain \(\lambda =-\frac{5}{9}\)
Obtain answer \(\frac{1}{3}\sqrt{2}\), or equivalent
Alternative method for question 9(c)
Use a scalar product to find the projection CN (or BN) of OC (or OB) on BC
Obtain answer \(CN=\frac{5}{3}\left ( or\ BN=\frac{14}{3} \right )\)
Use Pythagoras to find ON
Obtain answer \(\frac{1}{3}\sqrt{2}\), or equivalent
Question
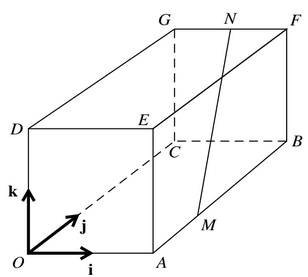
In the diagram, OABCDEFG is a cuboid in which OA=2 units, OC = 3 units and OD = 2 units. Unit vectors i, j and k are parellel to OA, OC and OD respectively. The point M on AB is such that MD = 2AM. The midpoint of FG is N.
(a) Express the vectors \(\overrightarrow{OM}\) and \(\overrightarrow{MN}\) in terms of i, j and k
(b) Find a vector equation for the line through M and N.
(c) Find the position vector of P, the foot of the perpendicular from D to the line through M and N.
Answer/Explanation
Ans:
(a) Obtain \(\overrightarrow{OM}=2i+j\)
Use a correct method to find \(\overrightarrow{MN}\)
Obtain \(\overrightarrow{MN}=-i+2j+2k\)
(b) Use a correct method to form an equation for MN
Obtain \(r=2i+j+ \lamdba(-i+2j+2k)\), or equivalent
(c) Find \(\overrightarrow{DP}\) for a point P on MN with parameter \(\lambda, e.g.(2- \lambda,1+2\lambda,-2+2\lambda)\)
Equate scalar product of \(\overrightarrow{DP}\) and a direction vector for MN to zero and solve for \(\lambda\).
Obtain\(\lambda=\frac{4}{9}\)
State that the position vector of P is \(\frac{14}{9}i+\frac{17}{9}j+\frac{8}{9}k\)
Two lines l and m have equations r = 3i + 2j + 5k + s(4i − j + 3k) and r = i − j − 2k + t(−i + 2j + 2k) respectively.
(a) Question
Show that l and m are perpendicular.
(b) Question
Show that l and m intersect and state the position vector of the point of intersection.
(c) Question
Show that the length of the perpendicular from the origin to the line m is \(\frac{1}{3}\sqrt{5}\) .
Answer/Explanation
Ans:(a)
Use correct method to evaluate the scalar product of relevant vectors
Obtain answer zero and deduce the given statement
Ans:(b)
Express general point of l or m in component form, e.g. (3 + 4s, 2 – s, 5 + 3s) or (1 – t, – 1 +2t, – 2 + 2t)
Equate at least two pairs of components and solve for s or for t
Obtain correct answer s = – 1 and t = 2
Verify that all three equations are satisfied
State position vector of the intersection – i + 3j +2k, or equivalent
Ans:(c)
Taking a general point P on m, form an equation in t by either equating a relevant scalar product to zero, or equating the derivative of \(\left | \overrightarrow{OP} \right |\) to zero, or taking a specific point Q on m, e.g. (1, – 1, – 2), using Pythagoras in triangle OPQ
Obtain t = \(\frac{7}{9}\)
Carry out correct method to find OP
Obtain \(\frac{\sqrt{5}}{3}\)
Question
With respect to the origin O, the points A, B, C, D have position vectors given by
\(\vec{OA}=i+3j+2k, \vec{OB}=2i+4j+k,\vec{OD}=-3i+j+2k\)
(i) Find the equation of the plane containing A, B and C, giving your answer in the form ax + by + cz = d.
(ii) The line through D parallel to OA meets the plane with equation x + 2y − z = 7 at the point P.
Find the position vector of P and show that the length of DP is\( 2\sqrt{14}\)
Answer/Explanation

(ii) Correctly form an equation for the line through D parallel to OA
Obtain a correct equation e.g \(r=-3i+j+2k+\lambda (i+3j+2k)\)
Substitute components in the equation of the plane and solve for λ
Obtain λ = 2 and position vector -i+7j+6k for p
Obtain the given answer correctly
Question
The line l has equation r = \(\begin{pmatrix}1\\2\\-1\\\end{pmatrix}+\lambda \begin{pmatrix}2\\1\\3\\\end{pmatrix}\) . The plane p has equation r. \(\begin{pmatrix}2\\-1\\-1\\\end{pmatrix}\) = 6.
(i) Show that l is parallel to p. [3]
(ii) A line m lies in the plane p and is perpendicular to l. The line m passes through the point with coordinates (5, 3, 1). Find a vector equation for m. [6]
Answer/Explanation
Ans:
(i) EITHER: Substitute for r in the given equation of p and expand scalar product
Obtain equation in λ in any correct form
Verify this is not satisfied for any value of λ
OR1: Substitute coordinates of a general point of l in the Cartesian equation of plane p
Obtain equation in λ in any correct form
Verify this is not satisfied for any value of λ
OR2: Expand scalar product of the normal to p and the direction vector of l
Verify scalar product is zero
Verify that one point of l does not lie in the plane
OR3: Use correct method to find the perpendicular distance of a general point of l from p
Obtain a correct unsimplified expression in terms of λ
Show that the perpendicular distance is 5/ √6 , or equivalent, for all λ
OR4: Use correct method to find the perpendicular distance of a particular point of l from p
Show that the perpendicular distance is 5/ √6 , or equivalent
Show that the perpendicular distance of a second point is also 5/ √6 , or equivalent
(ii) EITHER: Calling the unknown direction vector ai + bj + ck state equation 2a + b + 3c = 0
State equation 2a – b – c = 0
Solve for one ratio, e.g. a : b
Obtain ratio a : b : c = 1 : 4 : − 2, or equivalent
OR: Attempt to calculate the vector product of the direction vector of l and the normal vector of the plane p, e.g. (2i + j + 3k ) x (2i – j – k)
Obtain two correct components of the product
Obtain answer 2i + 8j – 4k , or equivalent
Form line equation with relevant vectors
Obtain answer r = 5i + 3j + k + µ (i + 4j – 2k), or equivalent
Question
The point P has coordinates (−1, 4, 11) and the line l has equation r = \(\begin{pmatrix}
1 & & \\
3& & \\
-4& &
\end{pmatrix}+\lambda \begin{pmatrix}
2
& & \\
1 & & \\
3 & &
\end{pmatrix}\)
(i) Find the perpendicular distance from P to l.
(ii) Find the equation of the plane which contains P and l, giving your answer in the form ax + by + cß = d, where a, b, c and d are integers.
Answer/Explanation

(ii) Either Use scalar product to obtain a relevant equation in a, b, c, e.g. 2a + b + 3c = 0 or
2a – b – 15c = 0
State two correct equations in a, b and c Solve simultaneous equations to obtain one ratio
Obtain a : b : c = –3 : 9 : –1 or equivalent
Obtain equation –3x + 9y – z = 28 or equivalent
Calculate vector product of two of
Obtain two correct components of the product
Obtain correct
Substitute in –3x + 9y – z = d to find d or equivalent
Obtain equation –3x + 9y – z = 28 or equivalent
Or 2 Form a two-parameter equation of the plane
Obtain r =
State three equations in x, y, z, s, t A1
Eliminate s and t
Obtain equation 3x – 9y + z = –28 or equivalent
Question
Relative to an origin O,the position vectors of points A and B are given by
\(\vec{OA}=\begin{pmatrix}3p\\ 4\\ p^{2}\end{pmatrix}\) and \(\vec{O}=\begin{pmatrix}-p\\ -1\\ p^{2}\end{pmatrix}\)
(i)Find the values of p for which angle AOB is \(90^{\circ}\)
(ii)For the case where p=3,find the unit vector in the direction of \(\vec{BA}\)
Answer/Explanation
(i) \(OA.OB=-3p^{2}-4+p^{4}\)
\(\left ( p^{2} +1\right )\left ( p^{2}-4 \right )=0\) with substitution
\(p\pm 2 \) and no other real solutions.
(ii) \(\vec{BA}=\begin{pmatrix}9\\ 4\\ 9\end{pmatrix}-\begin{pmatrix}-3\\ -1\\ 9\end{pmatrix}=\begin{pmatrix}12\\ 5\\ 0\end{pmatrix}\)
\(\left | \vec{BA} \right |=\sqrt{12^{2}+5^{2}}=13\) and division by thier 13
Unit vector \(=\frac{1}{13}\begin{pmatrix}12\\ 5\\ 0\end{pmatrix}\)
Question
Relative to an origin O,the position vectors of three points,A,B and C,are given by
\(\vec{OA}=i+2pj+qk\), \(\vec{OB}=qj-2qk\) and \(\vec{OC}=-\left ( 4p^{2} +q^{2}\right )i+2pj+qk\)
where p and q are constants.
(i)Show that \(\vec{OA}\) is perpendicular to \(\vec{OC}\) for all non-zero values of p and q.
(ii)Find the magnitude of \( \vec{CA}\) in terms of p and q.
(iii)For the case where p=3 and q=2 ,find the unit vector parallel to \(\vec{BA}\)
Answer/Explanation
(i)\(OA.OC=-4p^{2}-q^{2}+4p^{2}+q^{2}\)=0
(ii)\(CA=OA-OC=\left ( \pm \right )\left ( 1+4p^{2} +q^{2}\right )\)
\(\left | CA \right |=1+4p^{2}+q^{2}\)
(iii)\(BA=OA-OB=i+6j+2k-\left ( 2j-6k \right )\)
\(=\left ( \pm \right )\left ( i+4j+8k \right )\)
\(\frac{xi+yj+zk}{\sqrt{x^{2}+y^{2}+z^{2}}}\rightarrow \frac{1}{9}\left ( i+4j+8k \right )\)
Question
Two vectors u and v are such that \(u=\begin{pmatrix}p^{2}\\ -2\\ 6\end{pmatrix} \) and \(v=\begin{pmatrix}2\\ p-1\\ 2p+1\end{pmatrix} \),where p is a constant.
(i)Find the values of p for which u is perpendicular to v.
(ii)For the case where p=1,find the angle between the directions of u and v.
Answer/Explanation
(i) \(2p^{2}-2p+2+12p+6\rightarrow 2p^{2}+10p+8\)
u.v=0
\(\left ( p+1 \right )\left ( p+4 \right )=0\rightarrow p=-1\) or p=-4
(ii)u.v=2+0+18=20
\(\left | u \right |=\sqrt{41}\) or\( \left | v\right |=\sqrt{13}\)
\(20=\sqrt{41}\times \sqrt{13}\times \cos \Theta\)
\(\Theta =30.0^{\circ}\) or 0.523rad
Question
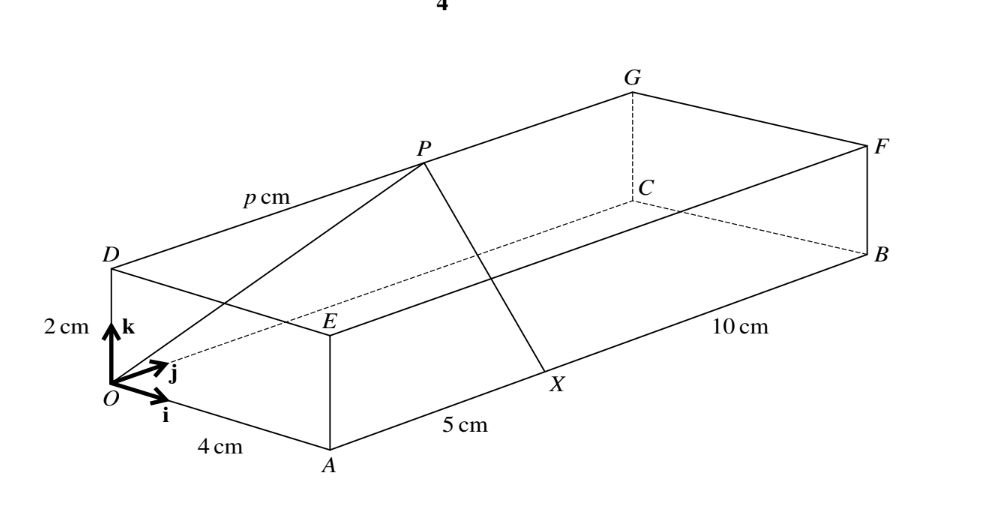
The diagram shows a cuboid OABCDEFG with a horizontal base OABC in which OA=4cm and AB=15cm.The height OD of the cuboid 2cm.The point X on AB is such that AX=5cm and the point P on DG is such that DP=p cm ,where p is a constant. Unit vectors i j and k are parallel to OA,OC and OD respectively.
(i) Find the possible values of p such that angle \(OPX=90^{\circ}\)
(ii)For the case where p=9,find the unit vector in the directioon of \(\vec{XP}\)
(iii) A point Q lies on the face CBFG and is such that XQ is parallel to AG.Find \(\vec{XQ}\).
Answer/Explanation
(i)XP=-4i+(p-5)j+2k
\(\left [ -4i+\left ( p-5 \right )j+2k\right ].\left ( pj+2k \right )=0\)
\(p^{2}-5p+4=0\0
p=1 or 4
(ii)XP=-4i+4j+2k\(\rightarrow \left | XP \right |=\sqrt{16+16+4}\)
Unit vector\(=\frac{1}{6}\left ( -4i+4j+2k \right )\)
(iii)AG=-4i+15j+2k
XQ\(=\Lambda AG\)
\(\Lambda =\frac{2}{3}\)
\(\rightarrow XQ=-\frac{8}{3}i+10j+\frac{4}{3}k\)
Question
(a) Relative to an origin O,the position vectors of two points P and Q are p and q respectively. The point R is such that PQR is straight line with Q the mid-point of PR.Find the positio0n vector of R in terms of p and q ,simplifying your answer.
(b)The vector 6i+aj+bk has magnitude 21 and perpendicular to 3i+2j+2k .Find the possible values of a and b ,showing all necessary working.
Answer/Explanation
(a)Either:
\(\vec{PR}=2\vec{PQ}=2(q-p)\)
\(\vec{OR}=p+2q-2p=2q-p\)
\(\vec{OR}=\vec{PQ}=q-p\)
\(\vec{OR}=\vec{OQ}+\vec{QR}=q+q-p=2q-p\)
(b)\(6^{2}+a^{2}+b^{2}=21^{2}\)
18+2a+2b=0
\(a^{2}+\left ( -a-9 \right )^{2}=405\)
\(\left ( 2 \right )\left ( a^{2}+9a-162 \right )\left (= 0 \right )\)
a=9 or -18
b=-18 0r 9
Question
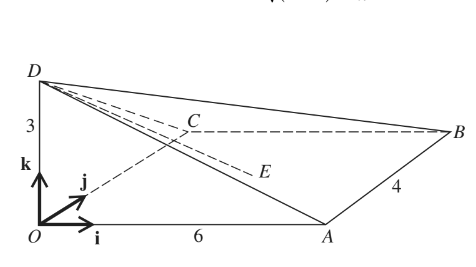
The diagram shows a pyramid OABCD in which the vertical edge OD is 3 units in length. The point E is the centre of the horizontal rectangular base OABC. The sides OA and AB have lengths of 6 units and 4 units respectively. The unit vectors i, j and k are parallel t0 \(\vec{OA}\),\(\vec{OC}\) and \(\vec{OD} \) respectively.
(i) Express each of the vectors \( \vec{DB}\) and \(\vec{DE}\) in terms of i, j and k.
(ii) Use a scalar product to find angle BDE.
Answer/Explanation
(i)BD=6i+4j-3k
DE=3i+2j-3k
(ii)DB.DE=18+8+9=35
\(\left | DB \right |=\sqrt{61}\) or \(\left | DE \right |=\sqrt{22}\)
\(35=\sqrt{61}\times \sqrt{22}\cos \Theta\)
\(\Theta =17.2^{\circ}\) (0.300rad)
Question
Relative to an origin O, the position vector of A is 3i + 2j − k and the position vector of B is 7i − 3j + k.
(i) Show that angle OAB is a right angle.
(ii) Find the area of triangle OAB.
Answer/Explanation
(i)AB or BA \(=\pm \left [ (7i-3j+k)-(3i+2j-k) \right ]=\pm \left ( 4i-5j+2k \right )\)
\((AO.AB)=\pm (12-10-2)\) (allow as column if total given )
=0 hence OAB=\(90^{\circ}\)
(ii)\(\left | OA \right |=\sqrt{9+4+1}=\sqrt{14}\)
\(\left | AB \right |=\sqrt{25+16+4}=\sqrt{45}\)
Area\( \Delta =\frac{1}{2}\sqrt{14}\sqrt{45}=12.5\)
Question
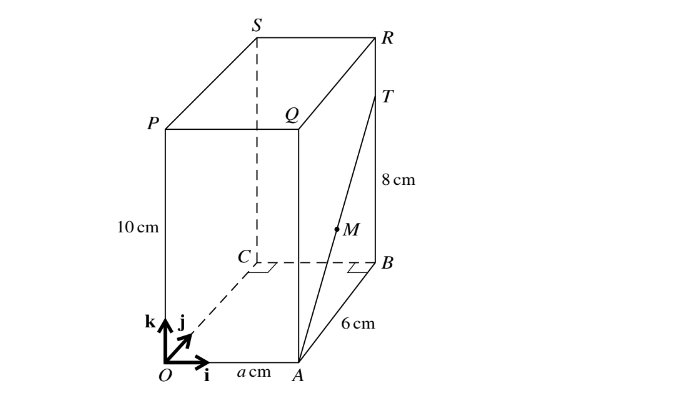
The diagram shows a cuboid OABCPQRS with a horizontal base OABC in which AB = 6 cm and OA = a cm, where a is a constant. The height OP of the cuboid is 10 cm. The point T on BR is such that BT = 8 cm, and M is the mid-point of AT. Unit vectors i, j and k are parallel to OA, OC and OP
respectively.
(i) For the case where a = 2, find the unit vector in the direction of \(\vec{PM}\)
(ii) For the case where angle \(ATP=\cos ^{-1}\left ( \frac{2}{7} \right )\) , find the value of a.
Answer/Explanation
(i)\(PM=2i-10k+\frac{1}{2}(6i+8k)\)
\(PM=2i+3j-6k\div \sqrt{4+9+36}\)
Unit vector\( =\frac{1}{2}(2i+3j-6k)\)
(ii)AT=6j+8k ,PT=ai+6j-2k
\(\cos ATP=\frac{(6i+8k)(ai+6j-2k)}{\sqrt{36+64}\sqrt{a^{2}+36+4}}\)
\(=\frac{36-16}{\sqrt{36+64}\sqrt{a^{2}+36+4}}\)
\(\frac{20}{10\sqrt{a^{2}+40}}\)
\(\frac{20}{10\sqrt{a^{2}+40}}=\frac{2}{7}\)
a=3