Question
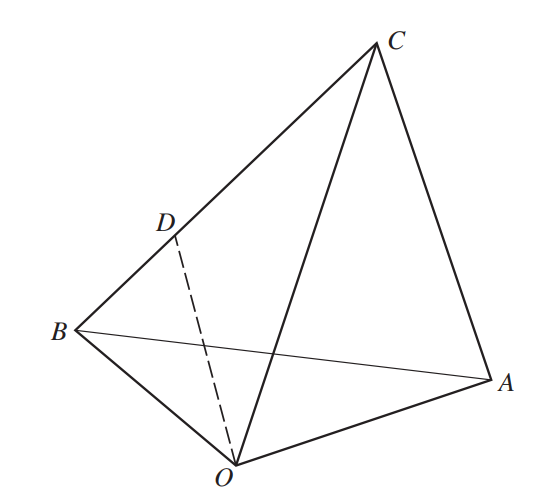
The diagram shows three points A, B and C whose position vectors with respect to the origin O are given by \(\underset{OA}{\rightarrow}=\begin{pmatrix}2\\-1\\2\\\end{pmatrix}, \underset{OB}{\rightarrow}=\begin{pmatrix}0\\3\\1\\\end{pmatrix}\) and \(\underset{OC}{\rightarrow}=\begin{pmatrix}3\\0\\4\\\end{pmatrix}\). The point D lies on BC, between B and C, and is such that CD = 2DB.
(i) Find the equation of the plane ABC, giving your answer in the form ax + by + cz = d. [6]
(ii) Find the position vector of D. [1]
(iii) Show that the length of the perpendicular from A to OD is \(\frac{1}{3}\sqrt{\left ( 65 \right )}\).[4]
Answer/Explanation
Ans:


Question
With respect to the origin O, the points A and B have position vectors given by \(\overrightarrow{OA}=\begin{pmatrix}1\\2\\ 1\end{pmatrix}\ and \ \overrightarrow{OB}=\begin{pmatrix}3\\1\\ -2\end{pmatrix}\). The line l has equation \(r=\begin{pmatrix}2\\3\\1\end{pmatrix}+\lambda \begin{pmatrix}1\\-2\\ 1\end{pmatrix}\).
(a) Find the acute angle between the directions of AB and l. [4]
(b) Find the position vector of the point P on l such that AP = BP. [5]
Answer/Explanation
Ans
(a) State or imply \(\overrightarrow{AB}=\begin{pmatrix}2\\-1 \\ -3\end{pmatrix}\)
Use the correct process to calculate the scalar product of a pair of relevant vectors, e.g. their
\(\overrightarrow{AB}\) and a direction vector for l
Using the correct process for the moduli, divide the scalar product by the
product of the moduli of the two vectors and evaluate the inverse cosine of
the result
Obtain answer 83.7° or 1.46 radians
(b) State or imply \(\pm \overrightarrow{AP}\ and \ \pm \overrightarrow{BP}\) in component form, i.e.
(1 +λ, 1 – 2λ, λ) and (– 1 +λ, 2 – 2λ, 3 +λ), or equivalent
Form an equation in λ by equating moduli or by using cos BAP = cos ABP
Obtain a correct equation in any form
(1+ λ)2+ (1- 2λ)2 + λ2=(λ – 1)2 + (2 – 2λ)2 + (λ + 3)2
Solve for λ and obtain position vector
Obtain correct position vector for P in any form, e.g. (8, – 9, 7) or 8i –9j + 7k
Question
Relative to the origin O,the position vectors of points A and B are given by
\(\vec{OA}=\begin{pmatrix}3\\ 0\\ -4\end{pmatrix}\) and \(\vec{OC}=\begin{pmatrix}6\\ -3\\ 2\end{pmatrix}\)
(i)Find the cosine of angle AOB.
The position vector of C is given by \(\vec{OC}=\begin{pmatrix}k\\ -2k\\ 2k-3\end{pmatrix}\)
(ii)Given that AB and OC have the same length,find the possible values of k.
Answer/Explanation
(i)OA.OB=18-8=10
Modulus of OA=5,OB=7
Angle AOB=\cos ^{-1}\left ( \frac{10}{35} \right )
\(\rightarrow \frac{10}{35}\) or \(\frac{2}{7}\)
(ii)\(\vec{AB}=b-a\begin{pmatrix}3\\ -3\\ 6\end{pmatrix}\)
\(k^{2}+4k^{2}+(2k-3)^{2}=9+9+36\)
\(\rightarrow 9k^{2}-12k-45=0\)
\(\rightarrow k=3\) or k=-\frac{5}{3}
Question
Relative to the origin O,the position vectors of points A and B are given by
\(\vec{OA}=\begin{pmatrix}3\\ 0\\ -4\end{pmatrix}\) and \(\vec{OC}=\begin{pmatrix}6\\ -3\\ 2\end{pmatrix}\)
(i)Find the cosine of angle AOB.
The position vector of C is given by \(\vec{OC}=\begin{pmatrix}k\\ -2k\\ 2k-3\end{pmatrix}\)
(ii)Given that AB and OC have the same length,find the possible values of k.
Answer/Explanation
(i)OA.OB=18-8=10
Modulus of OA=5,OB=7
Angle AOB=\cos ^{-1}\left ( \frac{10}{35} \right )
\(\rightarrow \frac{10}{35}\) or \(\frac{2}{7}\)
(ii)\(\vec{AB}=b-a\begin{pmatrix}3\\ -3\\ 6\end{pmatrix}\)
\(k^{2}+4k^{2}+(2k-3)^{2}=9+9+36\)
\(\rightarrow 9k^{2}-12k-45=0\)
\(\rightarrow k=3\) or k=-\frac{5}{3}
Question
Relative to an origin O,the position vectors of points A and B are given by
\(\vec{OA}=\begin{pmatrix}3p\\ 4\\ p^{2}\end{pmatrix}\) and \(\vec{O}=\begin{pmatrix}-p\\ -1\\ p^{2}\end{pmatrix}\)
(i)Find the values of p for which angle AOB is \(90^{\circ}\)
(ii)For the case where p=3,find the unit vector in the direction of \(\vec{BA}\)
Answer/Explanation
(i) \(OA.OB=-3p^{2}-4+p^{4}\)
\(\left ( p^{2} +1\right )\left ( p^{2}-4 \right )=0\) with substitution
\(p\pm 2 \) and no other real solutions.
(ii) \(\vec{BA}=\begin{pmatrix}9\\ 4\\ 9\end{pmatrix}-\begin{pmatrix}-3\\ -1\\ 9\end{pmatrix}=\begin{pmatrix}12\\ 5\\ 0\end{pmatrix}\)
\(\left | \vec{BA} \right |=\sqrt{12^{2}+5^{2}}=13\) and division by thier 13
Unit vector \(=\frac{1}{13}\begin{pmatrix}12\\ 5\\ 0\end{pmatrix}\)
Question
Relative to an origin O,the position vectors of three points,A,B and C,are given by
\(\vec{OA}=i+2pj+qk\), \(\vec{OB}=qj-2qk\) and \(\vec{OC}=-\left ( 4p^{2} +q^{2}\right )i+2pj+qk\)
where p and q are constants.
(i)Show that \(\vec{OA}\) is perpendicular to \(\vec{OC}\) for all non-zero values of p and q.
(ii)Find the magnitude of \( \vec{CA}\) in terms of p and q.
(iii)For the case where p=3 and q=2 ,find the unit vector parallel to \(\vec{BA}\)
Answer/Explanation
(i)\(OA.OC=-4p^{2}-q^{2}+4p^{2}+q^{2}\)=0
(ii)\(CA=OA-OC=\left ( \pm \right )\left ( 1+4p^{2} +q^{2}\right )\)
\(\left | CA \right |=1+4p^{2}+q^{2}\)
(iii)\(BA=OA-OB=i+6j+2k-\left ( 2j-6k \right )\)
\(=\left ( \pm \right )\left ( i+4j+8k \right )\)
\(\frac{xi+yj+zk}{\sqrt{x^{2}+y^{2}+z^{2}}}\rightarrow \frac{1}{9}\left ( i+4j+8k \right )\)
Question
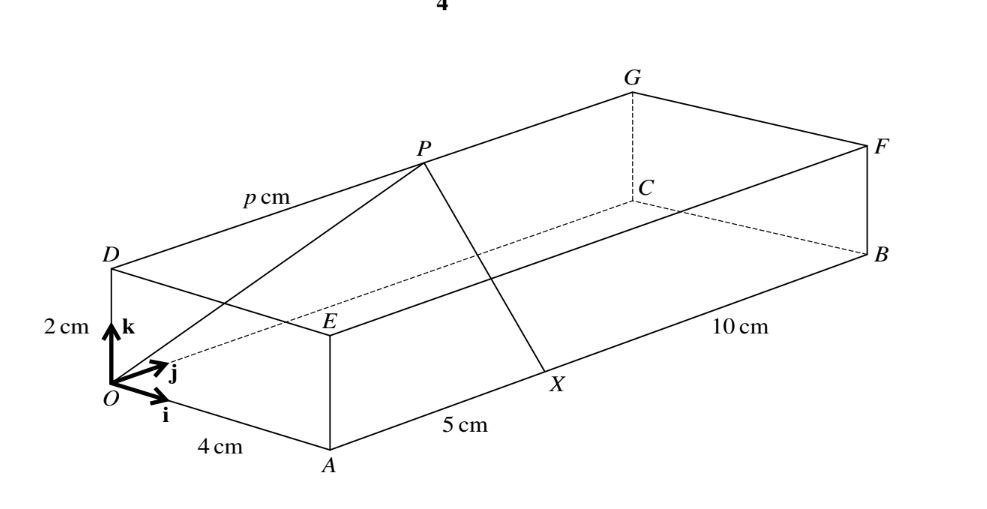
The diagram shows a cuboid OABCDEFG with a horizontal base OABC in which OA=4cm and AB=15cm.The height OD of the cuboid 2cm.The point X on AB is such that AX=5cm and the point P on DG is such that DP=p cm ,where p is a constant. Unit vectors i j and k are parallel to OA,OC and OD respectively.
(i) Find the possible values of p such that angle \(OPX=90^{\circ}\)
(ii)For the case where p=9,find the unit vector in the directioon of \(\vec{XP}\)
(iii) A point Q lies on the face CBFG and is such that XQ is parallel to AG.Find \(\vec{XQ}\).
Answer/Explanation
(i)XP=-4i+(p-5)j+2k
\(\left [ -4i+\left ( p-5 \right )j+2k\right ].\left ( pj+2k \right )=0\)
\(p^{2}-5p+4=0\0
p=1 or 4
(ii)XP=-4i+4j+2k\(\rightarrow \left | XP \right |=\sqrt{16+16+4}\)
Unit vector\(=\frac{1}{6}\left ( -4i+4j+2k \right )\)
(iii)AG=-4i+15j+2k
XQ\(=\Lambda AG\)
\(\Lambda =\frac{2}{3}\)
\(\rightarrow XQ=-\frac{8}{3}i+10j+\frac{4}{3}k\)
Question
(a) Relative to an origin O,the position vectors of two points P and Q are p and q respectively. The point R is such that PQR is straight line with Q the mid-point of PR.Find the positio0n vector of R in terms of p and q ,simplifying your answer.
(b)The vector 6i+aj+bk has magnitude 21 and perpendicular to 3i+2j+2k .Find the possible values of a and b ,showing all necessary working.
Answer/Explanation
(a)Either:
\(\vec{PR}=2\vec{PQ}=2(q-p)\)
\(\vec{OR}=p+2q-2p=2q-p\)
\(\vec{OR}=\vec{PQ}=q-p\)
\(\vec{OR}=\vec{OQ}+\vec{QR}=q+q-p=2q-p\)
(b)\(6^{2}+a^{2}+b^{2}=21^{2}\)
18+2a+2b=0
\(a^{2}+\left ( -a-9 \right )^{2}=405\)
\(\left ( 2 \right )\left ( a^{2}+9a-162 \right )\left (= 0 \right )\)
a=9 or -18
b=-18 0r 9
Question
The position vectors of points A and B relative to an origin O are a and b respectively. The position vectors of points C and D relative to O are 3a and 2b respectively. It is given that
\(a=\begin{pmatrix}2\\ 1\\ 2\end{pmatrix}\) and \(b=\begin{pmatrix}4\\ 0\\ 6\end{pmatrix}\)
(i) Find the unit vector in the direction of \(\vec{CD}\)
(ii) The point E is the mid-point of CD. Find angle EOD.
Answer/Explanation
(i)\(\vec{CD}=-3\begin{pmatrix}2\\ 1\\ 2\end{pmatrix}+2\begin{pmatrix}4\\ 0\\ 6\end{pmatrix}=\begin{pmatrix}2\\ -3\\ 6\end{pmatrix}\)
\(Unit vector =\frac{1}{7}\begin{pmatrix}2\\ -3\\ 6\end{pmatrix}\)
(ii)\(\vec{OE}=\begin{pmatrix}6\\ 3\\ 6\end{pmatrix}+\begin{pmatrix}1\\-1\tfrac{1}{2}\\ 3\end{pmatrix}=\begin{pmatrix}7\\ 1\tfrac{1}{2}\\ 9\end{pmatrix}\)
\(\vec{OE}.\vec{OD}=56+0+108=164\)
\(\left | \vec{OE} \right |=\sqrt{132.25}=11.5\)
\(\left | \vec{OD} \right |=\sqrt{208}\)
\(164=\sqrt{132.25}\times \sqrt{208}\times \cos \Theta\)
\(\Theta =8.6^{\circ}\)
Question
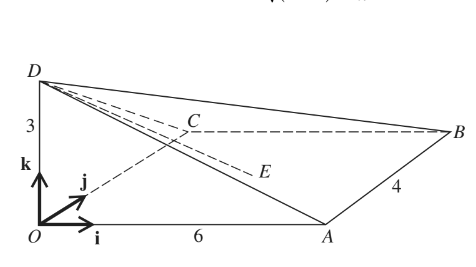
The diagram shows a pyramid OABCD in which the vertical edge OD is 3 units in length. The point E is the centre of the horizontal rectangular base OABC. The sides OA and AB have lengths of 6 units and 4 units respectively. The unit vectors i, j and k are parallel t0 \(\vec{OA}\),\(\vec{OC}\) and \(\vec{OD} \) respectively.
(i) Express each of the vectors \( \vec{DB}\) and \(\vec{DE}\) in terms of i, j and k.
(ii) Use a scalar product to find angle BDE.
Answer/Explanation
(i)BD=6i+4j-3k
DE=3i+2j-3k
(ii)DB.DE=18+8+9=35
\(\left | DB \right |=\sqrt{61}\) or \(\left | DE \right |=\sqrt{22}\)
\(35=\sqrt{61}\times \sqrt{22}\cos \Theta\)
\(\Theta =17.2^{\circ}\) (0.300rad)
Question
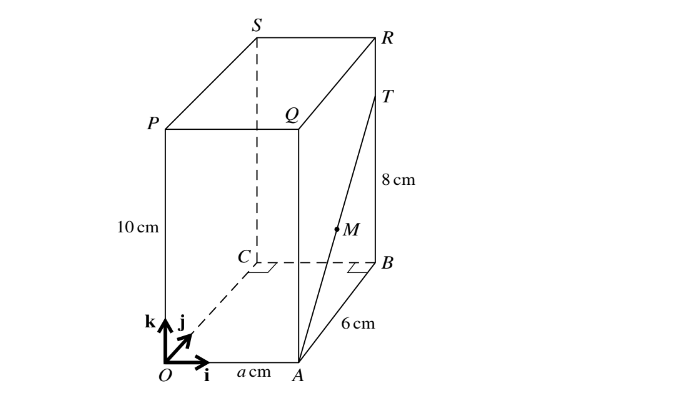
The diagram shows a cuboid OABCPQRS with a horizontal base OABC in which AB = 6 cm and OA = a cm, where a is a constant. The height OP of the cuboid is 10 cm. The point T on BR is such that BT = 8 cm, and M is the mid-point of AT. Unit vectors i, j and k are parallel to OA, OC and OP
respectively.
(i) For the case where a = 2, find the unit vector in the direction of \(\vec{PM}\)
(ii) For the case where angle \(ATP=\cos ^{-1}\left ( \frac{2}{7} \right )\) , find the value of a.
Answer/Explanation
(i)\(PM=2i-10k+\frac{1}{2}(6i+8k)\)
\(PM=2i+3j-6k\div \sqrt{4+9+36}\)
Unit vector\( =\frac{1}{2}(2i+3j-6k)\)
(ii)AT=6j+8k ,PT=ai+6j-2k
\(\cos ATP=\frac{(6i+8k)(ai+6j-2k)}{\sqrt{36+64}\sqrt{a^{2}+36+4}}\)
\(=\frac{36-16}{\sqrt{36+64}\sqrt{a^{2}+36+4}}\)
\(\frac{20}{10\sqrt{a^{2}+40}}\)
\(\frac{20}{10\sqrt{a^{2}+40}}=\frac{2}{7}\)
a=3