Question
The coordinates (x, y )of a general point on a curve satisfy the differential equation\( x\frac{dy}{dx}=(2-x^{2})y\)
The curve passes through the point (1, 1). Find the equation of the curve, obtaining an expression for
y in terms of x. [7]
Answer/Explanation
Separate variables correctly and integrate at least one side Obtain term ln y
Obtain terms 2 ln \(x-\frac{1}{2}x^{2}\)
Use x = 1, y = 1 to evaluate a constant, or as limits
Obtain correct solution in any form, e.g.\(In y=2 In x-\frac{1}{2}x^{2}+\frac{1}{2}\)
Rearrange as y=\(x^{2} exp (\frac{1}{2}-\frac{1}{2}x^{2})\) or equivalent
Question
The number of insects in a population t weeks after the start of observations is denoted by N. The population is decreasing at a rate proportional to \(Ne^{-0.02t}\)The variables N and t are treated as continuous, and it is given that when t = 0, N = 1000 and \(\frac{dN}{dt}\)=-10
(i) Show that N and t satisfy the differential equation \(\frac{dN}{dt}=-0.01e^{-0.02t}N\)
(ii) Solve the differential equation and find the value of t when N = 800.
(iii) State what happens to the value of N as t becomes large.
Answer/Explanation
(i) State\( \frac{dN}{dt}=ke^{-0.02t}\) N − and show k = – 0.01
(ii) Separate variables correctly and integrate at least one side
Obtain term ln N
Obtain term\( 0.5e^{-0.02t}\)
Use N = 1000, t = 0 to evaluate a constant, or as limits, in a solution with terms a N ln and \(be^{-0.02t}\) , where ab
≠ 0
Obtain correct solution in any form e.g. In N -1000= \(0.5(e^{-0.02t}-1)\) Substitute N = 800 and obtain t = 29.6
(iii) State that N approaches \(\frac{1000}{\sqrt{e}}\)
Question
(i) Differentiate \(\frac{1}{sin^{2}\Theta } \)with respect to\( \Theta \)
(ii) The variables x and 1 satisfy the differential equation\( xtan\Theta \frac{dx}{d\Theta }+cosec^{2}\)=0,
for 0 < 1 <\(\frac{1}{2}\)and x > 0. It is given that x = 4 when \(\Theta \frac{1}{6}\pi\).Solve the differential equation, obtaining an expression for x in terms of \(\Theta \)
Answer/Explanation
(i) Use chain rule Obtain correct answer in any form
(ii) Separate variables correctly and integrate at least one side Obtain term \(\frac{1}{2}x^{2}\)
Obtain term of the form \(\frac{k}{sin^{2}\Theta }\)
Use x = 4,\(\Theta =\frac{1}{6\Pi }\) to evaluate a constant, or as limits, in a solution with terms and \(ax^{2} and \frac{b}{sin^{2}\Theta }\) where ab
≠ 0 Obtain solution \(\sqrt{(cosec^{2}+12)}\)
Question
The variables x and y are related by the differential equation
\(\frac{dy}{dx}=\frac{6ye^{3x}}{2+e^{3x}}\)
Given that y = 36 when x = 0, find an expression for y in terms of x.
Answer/Explanation
Separate variables correctly and recognisable attempt at integration of at least one side
Obtain lny, or equivalent
Obtain
Use y(0) = 36 to find constant in
Obtain equation correctly without logarithms from
Obtain
Question
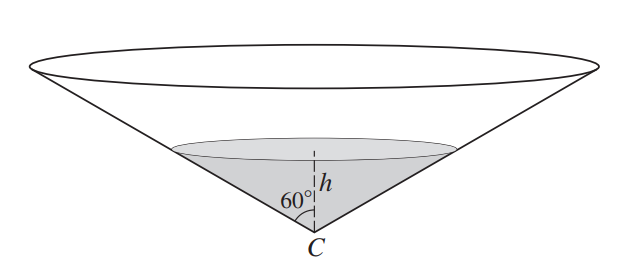
A tank containing water is in the form of a cone with vertex C. The axis is vertical and the semivertical angle is 60°, as shown in the diagram. At time t = 0, the tank is full and the depth of water is H. At this instant, a tap at C is opened and water begins to flow out. The volume of water in the tank decreases at a rate proportional to √h, where h is the depth of water at time t. The tank becomes empty when t = 60.
(i) Show that h and t satisfy a differential equation of the form
\(\frac{dh}{dt}=-Ah^{-\frac{3}{2}},\)
where A is a positive constant.[4]
(ii) Solve the differential equation given in part (i) and obtain an expression for t in terms of h and H.[6]
(iii) Find the time at which the depth reaches \(\frac{1}{2}H\).[1]
[The volume V of a cone of vertical height h and base radius r is given by \(V=\frac{1}{3}\pi r^{2}h.\) ]
Answer/Explanation
Ans:


Question
Liquid is flowing into a small tank which has a leak. Initially the tank is empty and, t minutes later, the volume of liquid in the tank is V cm3. The liquid is flowing into the tank at a constant rate of 80 cm3 per minute. Because of the leak, liquid is being lost from the tank at a rate which, at any instant, is equal to kV cm3 per minute where k is a positive constant.
(i) Write down a differential equation describing this situation and solve it to show that [7]
\(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\)
(ii) It is observed that V = 500 when t = 15, so that k satisfies the equation
\(k=\frac{4-4e^{-kt} }{25}\)
Use an iterative formula, based on this equation, to find the value of k correct to 2 significant figures. Use an initial value of k = 0.1 and show the result of each iteration to 4 significant figures. [3]
(iii) Determine how much liquid there is in the tank 20 minutes after the liquid started flowing, and state what happens to the volume of liquid in the tank after a long time.[2]
Answer/Explanation
Ans:
(i) State \(\frac{dV}{dt}=80-kV\)
Correctly separate variables and attempt integration of one side
Obtain a ln(80 − kV) = t or equivalent
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t\) or equivalent
Use t = 0 and V = 0 to find constant of integration or as limits
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t-\frac{1}{k}\) or equivalent
Obtain given answer \(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\) correctly
(ii) Use iterative formula correctly at least once
Obtain final answer 0.14
Show sufficient iterations to 4 s.f. to justify answer to 2 s.f. or show a sign change in the interval (0.135, 0.145)
(iii) State a value between 530 and 540 cm3 inclusive
State or imply that volume approaches 569 cm3 (allowing any value between 567 and 571 inclusive)
Question
The variables x and y satisfy the differential equation \(\frac{dy}{dx}=4cos^{2}ytanx.for 0\leqslant x< \frac{1}{2}\pi , and x=0 when y=\frac{1}{4}\pi \),Solve this differential equation and find the value of x when \(\frac{1}{3}\pi \)
Answer/Explanation
Separate variables correctly and attempt integration of one side Obtain term tan y , or equivalent
Obtain term of the form k x ln cos , or equivalent
Obtain term −4ln cos x , or equivalent Use x = 0 and y =\(\frac{1}{4} π\) in solution containing a y tan and b x ln cos to evaluate a constant, or as limits Obtain correct solution in any form, e.g. tan 4ln secx+1 Substitute y =\(\frac{1}{3} π\) in solution containing terms a y tan and b x ln cos , and use correct
method to find x Obtain answer x = 0.587
Question
The coordinates (x, y) of a general point of a curve satisfy the differential equation
\(x\frac{dy}{dx}=(1-2x^{2})y,\)
for x > 0. It is given that y = 1 when x = 1.
Solve the differential equation, obtaining an expression for y in terms of x. [6]
Answer/Explanation
Separate variables correctly and attempt integration of at least
one side
Obtain term ln y
Obtain terms 2 ln x − x2
Use x = 1, y = 1 to evaluate a constant, or as limits, in a solution
containing at least 2 terms of the form a ln y , b ln x and cx2
Obtain correct solution in any form
Rearrange and obtain \(y=xe^{1-x^{2}}\)
Question
A certain curve is such that its gradient at a point (x, y) is proportional to \(\frac{y}{x\sqrt{x}}\). The curve passes
through the points with coordinates (1, 1) and (4, e).
(a) By setting up and solving a differential equation, find the equation of the curve, expressing y in
terms of x. [8]
(b) Describe what happens to y as x tends to infinity. [1]
Answer/Explanation
Ans
(a) State \(\frac{dy}{dx}=k\frac{y}{x\sqrt{x}}\), or equivalent
Separate variables correctly and attempt integration of at least one side M1
Obtain term ln y, or equivalent
Obtain term \(-2k\frac{1}{\sqrt{x}}\), or equivalent
Use given coordinates to find k or a constant of integration c in a solution containing terms of the form a ln y and \(\frac{b}{\sqrt{x}}\), where ab≠ 0
Obtain k = 1 and c = 2
Obtain final answer y = exp \(\left ( -\frac{2}{\sqrt{x}}+2 \right )\), or equivalent
(b) State that y approaches e2
(FT their c in part (a) of the correct form)
Question
The variables x and y satisfy the differential equation
\(\frac{dy}{dx}=\frac{1+4y^2}{e^x}\).
It is given that y=0 when x = 1.
(a) Solve the differential equation, obtaining an expression for y in terms of x.
(b) State what happens to the value of y as x tends to infinity.
Answer/Explanation
Ans:
(a) Separate variables correctly and attempt integration of at least one side
Obtain term of the form \(atan^{-1}(2y)\)
Obtain term \(\frac{1}{2}tan^{-1}(2y)\)
Obtain term \(-e^{-x}\)
Use x = 1, y = 0 to evaluate a constant or as limits in a solution containing
terms of the form \(atan^{-1}(by)\) and \(ce^{\pm x}\)
Obtain correct answer in any form
Obtain final answer \(y=\frac{1}{2}tan(2e^{-1}-2e^{-x})\), or equivalent
(b) State that y approaches \(\frac{1}{2}tan(2e^{-1})\), or equivalent
Question
(a)Given that y = ln ( ln x), show that
\(\frac{dy}{dx} = \frac{1}{x ln x}.\)
The variables x and t satisfy the differential equation
x ln x + t \(\frac{dx}{dt} = 0\)
It is given that x = e when t = 2.
(b)Solve the differential equation obtaining an expression for x in terms of t, simplifying your answer.
(c)Hence state what happens to the value of x as t tends to infinity.
Answer/Explanation
Ans:
(a)Show sufficient working to justify the given answer
(b)Correct separation of variables
Obtain term ln ( ln x)
Obtain term −ln t
Evaluate a constant or use x = e and t = 2 as limits in an expression involving ln (ln x)
Obtain correct solution in any form, e.g. ln (ln x) =− ln t + ln 2
Use log laws to enable removal of logarithms
Obtain answer \(x = e^{\frac{2}{t}}\) , or simplified equivalent
(c) State that x tends to 1 coming from \(x = e^{\frac{k}{t}}\)
Question
The variables x and y satisfy the differential equation
\((1-cosx)\frac{dy}{dx}=y sin x\).
It is given that y=4 when \(x=\pi\).
(a) Solve the differential equation, obtaining an expression for y in terms of x.
(b) Sketch the graph of y against x for \(0<x<2\pi\)
Answer/Explanation
Ans:
- Separate variables correctly and attempt integration of at least one side
Obtain term In y
Obtain term of the form ±In(1-cosx)
Obtain term In(1-cosx)
Use \(x=\pi,y=4\) to evaluate a constant, or as limits, in a solution containing terms of the form aIn y and bIn(1-cos x)
Obtain final answer y = 2(1-cosx) - Show a correct graph for \(0<x<2\pi\) with the maximum at \(x=\pi\)
Question
A large field of area 4 km2 is becoming infected with a soil disease. At time t years the area infected is x km2 and the rate of growth of the infected area is given by the differential equation dx
dt= kx 4 − x,
where k is a positive constant. It is given that when t = 0, x = 0.4 and that when t = 2, x = 2.
(i) Solve the differential equation and show that k = 1/4ln 3.
(ii) Find the value of t when 90% of the area of the field is infected.
Answer/Explanation

Question
The variables x and y satisfy the differential equation
\(x\frac{dy}{dx}=y(1-2x^{2})\)
and it is given that y = 2 when x = 1. Solve the differential equation and obtain an expression for y in
terms of x in a form not involving logarithms.
Answer/Explanation
Separate variables and attempt integration of at least one side
Obtain term ln y
Obtain terms
Use x = 1 and y =2 to evaluate a constant, or as limits
Obtain correct solution in any form, e.g. 2 ln ln
Obtain correct expression for y, free of logarithms, i.e. \(y= 2x exp(1-x^{2})\)
Question
The variables x and y satisfy the differential equation
\(\left ( x + 1 \right ) \left ( 3x + 1 \right )\frac{dy}{dx}= y,\)
and it is given that y = 1 when x = 1.
Solve the differential equation and find the exact value of y when x = 3, giving your answer in a simplified form.
Answer/Explanation
Ans:
Correctly separate variables and integrate at least one side
Obtain term ln y from integral of 1/y
State or imply the form \(\frac{A}{x+1} + \frac{B}{3x+1}\) and use a correct method to find a constant
Obtain \(A = -\frac{1}{2} and B = \frac{3}{2}\)
Obtain terms ![]() or combination of these terms
or combination of these terms
Use x = 1 and y = 1 to evaluate a constant, or expression for a constant, (decimal equivalent of ln terms allowed) or as limits, in a solution containing terms a ln y, b ln (x+1) and c ln (3x+1), where abc ≠ 0
Obtain an expression for y or y2 and substitute x = 3
Obtain answer y = \(\frac{1}{2}\sqrt{5} or \sqrt{\frac{5}{4}} or \sqrt{\frac{10}{8}}\)
Question
The variables x and y are related by the differential equation
\(x\frac{dy}{dx}=1-y^{2}\)
When x = 2, y = 0. Solve the differential equation, obtaining an expression for y in terms of x.
Separate variables correctly and attempt integration of one side
Obtain term ln x
Answer/Explanation
State or imply\( \frac{1}{1-y^{2}}\equiv \frac{A}{1-y}+\frac{B}{1+y}\) and use a relevant method to find A or B
Obtain A\(=\frac{1}{2},B\)=\(\frac{1}{2}\)
Integrate and obtain\(-\frac{1}{2} In(1-y)+\frac{1}{2}In(1+y)\),or equivalent
[If the integral is directly stated as\( k_{1}\) In(\frac{1+y}{1-y}) \)or \(K_{2} \)In(\frac{1-y}{1+y})\) give , and then A2 for \(k_{1} or k_{2}\)=\(-\frac{1}{2}\)
Evaluate a constant, or use limits x = 2, y = 0 in a solution containing terms a ln x, b ln (1 – y) and c ln (1 + y), where\( abc\neq 0\)
[This M mark is not available if the integral of \(1/(1 – y^{2}) \)is initially taken to be of the form k ln \((1 – y^{2})\)]
Obtain solution in any correct form, e.g.\(\frac{1}{2} In(\frac{1+y}{1-y})\) = Inx-In2
Rearrange and obtain y=\(\frac{x^{2}-4}{x^{2}+4}\) ,or equivalent, free of logarithms
Question
The variables x and y are related by the differential equation \(\frac{dy}{dx}=\frac{6xe^{3x}}{y^{2}}\) It is given that y = 2 when x = 0. Solve the differential equation and hence find the value of y when x = 0.5, giving your answer correct to 2 decimal places
Answer/Explanation
.
Separate variables correctly and attempt integration on at least one side
Obtain \(\frac{1}{3}y^{3}\)
y or equivalent on left-hand side
Use integration by parts on right-hand side (as far as \(axe^{3x}+\int be^{3x}dx\)
Obtain or imply\(9 2xe^{3x}-\frac{2}{3}e^{3x}\)
Obtain
\(2xe^{3x}-\frac{2}{3}e^{3x}\)
Substitute x = 0, y = 2 in an expression containing terms where ABC ≠ 0, and
find the value of c
Obtain\( \frac{1}{3}y^{3}=2xe^{3x}-\frac{2}{3}e^{3x}+\frac{10}{3}\) or equivalent
Substitute x = 0.5 to obtain y = 2.44
Question
The variables x and y satisfy the differential equation
\(\frac{dy}{dx}=xe^{x+y},\)
and it is given that y = 0 when x = 0.
(i) Solve the differential equation and obtain an expression for y in terms of x. [7]
(ii) Explain briefly why x can only take values less than 1. [1]
Answer/Explanation
Ans:
(i) Separate variables and attempt integration of one side
Obtain term -e-y
Integrate xex by parts reaching \(xe^{x}+\int e^{x} dx\)
Obtain integral xex -ex
Evaluate a constant, or use limits x = 0, y = 0
Obtain correct solution in any form
Obtain final answer y=-ln(ex(1-x)), or equivalent
(ii) Justify the given statement B1 [1]
Question
Liquid is flowing into a small tank which has a leak. Initially the tank is empty and, t minutes later, the volume of liquid in the tank is V cm3. The liquid is flowing into the tank at a constant rate of 80 cm3 per minute. Because of the leak, liquid is being lost from the tank at a rate which, at any instant, is equal to kV cm3 per minute where k is a positive constant.
(i) Write down a differential equation describing this situation and solve it to show that [7]
\(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\)
(ii) It is observed that V = 500 when t = 15, so that k satisfies the equation
\(k=\frac{4-4e^{-kt} }{25}\)
Use an iterative formula, based on this equation, to find the value of k correct to 2 significant figures. Use an initial value of k = 0.1 and show the result of each iteration to 4 significant figures. [3]
(iii) Determine how much liquid there is in the tank 20 minutes after the liquid started flowing, and state what happens to the volume of liquid in the tank after a long time.[2]
Answer/Explanation
Ans:
(i) State \(\frac{dV}{dt}=80-kV\)
Correctly separate variables and attempt integration of one side
Obtain a ln(80 − kV) = t or equivalent
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t\) or equivalent
Use t = 0 and V = 0 to find constant of integration or as limits
Obtain \(-\frac{1}{k}ln\left ( 80-kV \right )=t-\frac{1}{k}\) or equivalent
Obtain given answer \(V=\frac{1}{k}\left ( 80-80e^{-kt} \right )\) correctly
(ii) Use iterative formula correctly at least once
Obtain final answer 0.14
Show sufficient iterations to 4 s.f. to justify answer to 2 s.f. or show a sign change in the interval (0.135, 0.145)
(iii) State a value between 530 and 540 cm3 inclusive
State or imply that volume approaches 569 cm3 (allowing any value between 567 and 571 inclusive)
Question
The variables x and y satisfy the differential equation \(\frac{dy}{dx}=4cos^{2}ytanx.for 0\leqslant x< \frac{1}{2}\pi , and x=0 when y=\frac{1}{4}\pi \),Solve this differential equation and find the value of x when \(\frac{1}{3}\pi \)
Answer/Explanation
Separate variables correctly and attempt integration of one side Obtain term tan y , or equivalent
Obtain term of the form k x ln cos , or equivalent
Obtain term −4ln cos x , or equivalent Use x = 0 and y =\(\frac{1}{4} π\) in solution containing a y tan and b x ln cos to evaluate a constant, or as limits Obtain correct solution in any form, e.g. tan 4ln secx+1 Substitute y =\(\frac{1}{3} π\) in solution containing terms a y tan and b x ln cos , and use correct
method to find x Obtain answer x = 0.587
Question
The coordinates (x, y) of a general point of a curve satisfy the differential equation
\(x\frac{dy}{dx}=(1-2x^{2})y,\)
for x > 0. It is given that y = 1 when x = 1.
Solve the differential equation, obtaining an expression for y in terms of x. [6]
Answer/Explanation
Separate variables correctly and attempt integration of at least
one side
Obtain term ln y
Obtain terms 2 ln x − x2
Use x = 1, y = 1 to evaluate a constant, or as limits, in a solution
containing at least 2 terms of the form a ln y , b ln x and cx2
Obtain correct solution in any form
Rearrange and obtain \(y=xe^{1-x^{2}}\)
Question
A certain curve is such that its gradient at a point (x, y) is proportional to \(\frac{y}{x\sqrt{x}}\). The curve passes
through the points with coordinates (1, 1) and (4, e).
(a) By setting up and solving a differential equation, find the equation of the curve, expressing y in
terms of x. [8]
(b) Describe what happens to y as x tends to infinity. [1]
Answer/Explanation
Ans
(a) State \(\frac{dy}{dx}=k\frac{y}{x\sqrt{x}}\), or equivalent
Separate variables correctly and attempt integration of at least one side M1
Obtain term ln y, or equivalent
Obtain term \(-2k\frac{1}{\sqrt{x}}\), or equivalent
Use given coordinates to find k or a constant of integration c in a solution containing terms of the form a ln y and \(\frac{b}{\sqrt{x}}\), where ab≠ 0
Obtain k = 1 and c = 2
Obtain final answer y = exp \(\left ( -\frac{2}{\sqrt{x}}+2 \right )\), or equivalent
(b) State that y approaches e2
(FT their c in part (a) of the correct form)
Question
The variables x and y satisfy the differential equation
\(\frac{dy}{dx}=\frac{1+4y^2}{e^x}\).
It is given that y=0 when x = 1.
(a) Solve the differential equation, obtaining an expression for y in terms of x.
(b) State what happens to the value of y as x tends to infinity.
Answer/Explanation
Ans:
(a) Separate variables correctly and attempt integration of at least one side
Obtain term of the form \(atan^{-1}(2y)\)
Obtain term \(\frac{1}{2}tan^{-1}(2y)\)
Obtain term \(-e^{-x}\)
Use x = 1, y = 0 to evaluate a constant or as limits in a solution containing
terms of the form \(atan^{-1}(by)\) and \(ce^{\pm x}\)
Obtain correct answer in any form
Obtain final answer \(y=\frac{1}{2}tan(2e^{-1}-2e^{-x})\), or equivalent
(b) State that y approaches \(\frac{1}{2}tan(2e^{-1})\), or equivalent
Question
(a)Given that y = ln ( ln x), show that
\(\frac{dy}{dx} = \frac{1}{x ln x}.\)
The variables x and t satisfy the differential equation
x ln x + t \(\frac{dx}{dt} = 0\)
It is given that x = e when t = 2.
(b)Solve the differential equation obtaining an expression for x in terms of t, simplifying your answer.
(c)Hence state what happens to the value of x as t tends to infinity.
Answer/Explanation
Ans:
(a)Show sufficient working to justify the given answer
(b)Correct separation of variables
Obtain term ln ( ln x)
Obtain term −ln t
Evaluate a constant or use x = e and t = 2 as limits in an expression involving ln (ln x)
Obtain correct solution in any form, e.g. ln (ln x) =− ln t + ln 2
Use log laws to enable removal of logarithms
Obtain answer \(x = e^{\frac{2}{t}}\) , or simplified equivalent
(c) State that x tends to 1 coming from \(x = e^{\frac{k}{t}}\)
Question
The variables x and y satisfy the differential equation
\((1-cosx)\frac{dy}{dx}=y sin x\).
It is given that y=4 when \(x=\pi\).
(a) Solve the differential equation, obtaining an expression for y in terms of x.
(b) Sketch the graph of y against x for \(0<x<2\pi\)
Answer/Explanation
Ans:
- Separate variables correctly and attempt integration of at least one side
Obtain term In y
Obtain term of the form ±In(1-cosx)
Obtain term In(1-cosx)
Use \(x=\pi,y=4\) to evaluate a constant, or as limits, in a solution containing terms of the form aIn y and bIn(1-cos x)
Obtain final answer y = 2(1-cosx) - Show a correct graph for \(0<x<2\pi\) with the maximum at \(x=\pi\)
Question
A large field of area 4 km2 is becoming infected with a soil disease. At time t years the area infected is x km2 and the rate of growth of the infected area is given by the differential equation dx
dt= kx 4 − x,
where k is a positive constant. It is given that when t = 0, x = 0.4 and that when t = 2, x = 2.
(i) Solve the differential equation and show that k = 1/4ln 3.
(ii) Find the value of t when 90% of the area of the field is infected.
Answer/Explanation

Question
The variables x and y satisfy the differential equation
\(x\frac{dy}{dx}=y(1-2x^{2})\)
and it is given that y = 2 when x = 1. Solve the differential equation and obtain an expression for y in
terms of x in a form not involving logarithms.
Answer/Explanation
Separate variables and attempt integration of at least one side
Obtain term ln y
Obtain terms
Use x = 1 and y =2 to evaluate a constant, or as limits
Obtain correct solution in any form, e.g. 2 ln ln
Obtain correct expression for y, free of logarithms, i.e. \(y= 2x exp(1-x^{2})\)
Question
The variables x and y satisfy the differential equation
\(\left ( x + 1 \right ) \left ( 3x + 1 \right )\frac{dy}{dx}= y,\)
and it is given that y = 1 when x = 1.
Solve the differential equation and find the exact value of y when x = 3, giving your answer in a simplified form.
Answer/Explanation
Ans:
Correctly separate variables and integrate at least one side
Obtain term ln y from integral of 1/y
State or imply the form \(\frac{A}{x+1} + \frac{B}{3x+1}\) and use a correct method to find a constant
Obtain \(A = -\frac{1}{2} and B = \frac{3}{2}\)
Obtain terms ![]() or combination of these terms
or combination of these terms
Use x = 1 and y = 1 to evaluate a constant, or expression for a constant, (decimal equivalent of ln terms allowed) or as limits, in a solution containing terms a ln y, b ln (x+1) and c ln (3x+1), where abc ≠ 0
Obtain an expression for y or y2 and substitute x = 3
Obtain answer y = \(\frac{1}{2}\sqrt{5} or \sqrt{\frac{5}{4}} or \sqrt{\frac{10}{8}}\)
Question
The variables x and y are related by the differential equation
\(x\frac{dy}{dx}=1-y^{2}\)
When x = 2, y = 0. Solve the differential equation, obtaining an expression for y in terms of x.
Separate variables correctly and attempt integration of one side
Obtain term ln x
Answer/Explanation
State or imply\( \frac{1}{1-y^{2}}\equiv \frac{A}{1-y}+\frac{B}{1+y}\) and use a relevant method to find A or B
Obtain A\(=\frac{1}{2},B\)=\(\frac{1}{2}\)
Integrate and obtain\(-\frac{1}{2} In(1-y)+\frac{1}{2}In(1+y)\),or equivalent
[If the integral is directly stated as\( k_{1}\) In(\frac{1+y}{1-y}) \)or \(K_{2} \)In(\frac{1-y}{1+y})\) give , and then A2 for \(k_{1} or k_{2}\)=\(-\frac{1}{2}\)
Evaluate a constant, or use limits x = 2, y = 0 in a solution containing terms a ln x, b ln (1 – y) and c ln (1 + y), where\( abc\neq 0\)
[This M mark is not available if the integral of \(1/(1 – y^{2}) \)is initially taken to be of the form k ln \((1 – y^{2})\)]
Obtain solution in any correct form, e.g.\(\frac{1}{2} In(\frac{1+y}{1-y})\) = Inx-In2
Rearrange and obtain y=\(\frac{x^{2}-4}{x^{2}+4}\) ,or equivalent, free of logarithms
Question
The variables x and y are related by the differential equation \(\frac{dy}{dx}=\frac{6xe^{3x}}{y^{2}}\) It is given that y = 2 when x = 0. Solve the differential equation and hence find the value of y when x = 0.5, giving your answer correct to 2 decimal places
Answer/Explanation
.
Separate variables correctly and attempt integration on at least one side
Obtain \(\frac{1}{3}y^{3}\)
y or equivalent on left-hand side
Use integration by parts on right-hand side (as far as \(axe^{3x}+\int be^{3x}dx\)
Obtain or imply\(9 2xe^{3x}-\frac{2}{3}e^{3x}\)
Obtain
\(2xe^{3x}-\frac{2}{3}e^{3x}\)
Substitute x = 0, y = 2 in an expression containing terms where ABC ≠ 0, and
find the value of c
Obtain\( \frac{1}{3}y^{3}=2xe^{3x}-\frac{2}{3}e^{3x}+\frac{10}{3}\) or equivalent
Substitute x = 0.5 to obtain y = 2.44
Question
The variables x and y satisfy the differential equation
\(\frac{dy}{dx}=xe^{x+y},\)
and it is given that y = 0 when x = 0.
(i) Solve the differential equation and obtain an expression for y in terms of x. [7]
(ii) Explain briefly why x can only take values less than 1. [1]
Answer/Explanation
Ans:
(i) Separate variables and attempt integration of one side
Obtain term -e-y
Integrate xex by parts reaching \(xe^{x}+\int e^{x} dx\)
Obtain integral xex -ex
Evaluate a constant, or use limits x = 0, y = 0
Obtain correct solution in any form
Obtain final answer y=-ln(ex(1-x)), or equivalent
(ii) Justify the given statement B1 [1]