Question
(a) Define gravitational potential. [2]
(b) The Earth E and the Moon M can both be considered as isolated point masses at their centres. The mass of the Earth is 5.98 × 1024 kg and the mass of the Moon is 7.35 × 1022 kg. The Earth and the Moon are separated by a distance of 3.84 × 108m, as shown in Fig. 2.1.
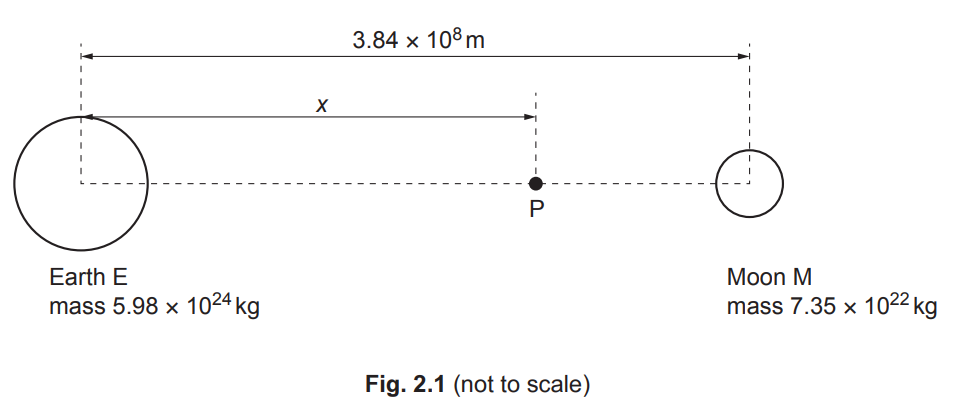
P is a point, on the line joining the centres of E and M, where the resultant gravitational field strength is zero. Point P is at a distance x from the centre of the Earth.
(i) Explain how it is possible for the gravitational field strength to be zero despite the presence of two large masses nearby. [2]
(ii) Show that x is approximately 3.5 × 108m. [2]
(iii) Calculate the gravitational potential φ at point P.
φ = ……………………………………….. J kg–1 [3]
[Total: 9]
Answer/Explanation
Ans
(a) work done per unit mass
(work done in) moving mass from infinity
(b) (i) (gravitational) fields from the Earth and Moon are in opposite directions
(resultant is zero where gravitational) fields are equal (in magnitude)
(b) (ii) \(g\infty M/r^{2}\)
5.98 × 1024 / x2 = 7.35 × 1022 / (3.84 × 108 – x)2
leading to x = 3.5 × 108 (m)
(b) (iii) φ (Earth) = (–)6.67 × 10–11 × (5.98 × 1024 / 3.5 × 108)
and
φ (Moon) = (–)6.67 × 10–11 × (7.35 × 1022 / 0.38 × 108)
φ = (–)6.67 × 10–11 × [(5.98 × 1024 / 3.5 × 108) + (7.35 × 1022 / 0.38 × 108)]
= – 1.3 × 106 J kg
Question
(a) State a similarity between the gravitational field lines around a point mass and the electric field lines around a point charge. [1]
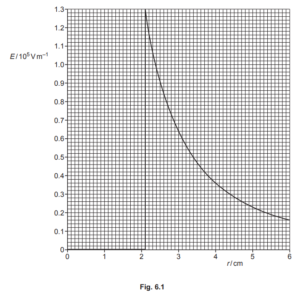
(b) The variation with radius r of the electric field strength E due to an isolated charged sphere in a vacuum is shown in Fig. 6.1.
Use data from Fig. 6.1 to:
(i) state the radius of the sphere
radius = …………………………………………… cm [1]
(ii) calculate the charge on the sphere.
charge = …………………………………………….. C [2]
(c) Using the formula for the electric potential due to an isolated point charge, determine the capacitance of the sphere in (b).
capacitance = ……………………………………………… F [3]
[Total: 7]
Answer/Explanation
Ans
(a) (both have) radial field lines
(b) (i) 2.1 cm
(b) (ii) \(E=\frac{Q}{4\pi \varepsilon _{o}r^{2}}\)
e.g. r = 2.1 cm, E = 1.30 × 105 V m–1
\(Q=4\pi \varepsilon_{o}r^{2}E\)
\(=4\times \pi \times 8.85\times 10^{-12}\times 0.021^{2}\times 1.30\times 10^{5}\)
\(=6.4\times 10^{-9}C\)