Question
In an X-ray tube, electrons are accelerated through a potential difference of \(75\) kV. The electrons then strike a tungsten target of effective mass \(15\) g.
The electron energy is converted into the energy of X-ray photons with an efficiency of \(5.0\) %. The rest of the energy is converted into thermal energy.
(a) The X-ray tube produces an image using a current of \(0.40\) A for a time of \(20\) ms.
The specific heat capacity of tungsten is \(130\, J\, kg^{–1}\, K^{–1}\).
Determine the temperature rise ΔT of the tungsten target.
(b) The linear attenuation coefficient of the X-ray photons in muscle is \(0.22\, cm^{–1}\).
Calculate the thickness t of muscle that will absorb \(80\) % of the incident X-ray intensity.
(c) Table 10.1 shows the linear attenuation coefficient μ for the X-ray photons in different tissues.
Table 10.1
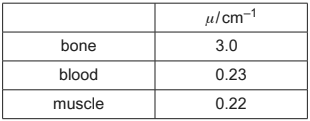
Two X-ray images are taken, one of equal thicknesses of bone and muscle and another of equal thicknesses of blood and muscle.
Explain why one of these images has good contrast, but the other does not.
Answer/Explanation
Ans:
(a) energy = mc ΔT
energy = ItV
\((\Delta T =)\frac{0.40 \times 0.020 \times 75\, 000 \times 0.95}{0.015 \times 130}\)
= \(290\) K
(b) \(I\) = \(I_{0}e^{-\mu t}\)
\(0.20\) = \(e^{-0.22t}\)
\(t\) = \(7.3\) cm
(c) either
(linear) attenuation coefficients / μ very different for bone and muscle
(very) different amounts (of X-rays) absorbed so good contrast
or (very) different intensities transmitted so good contrast
or
(linear) attenuation coefficients / μ similar for blood and muscle
similar amounts (of X-rays) absorbed so poor contrast
Question
(a) Define specific heat capacity. [2]
(b) A sealed container of fixed volume V contains N molecules, each of mass m, of an ideal gas at pressure p.
(i) State an expression, in terms of V, N, p and the Boltzmann constant k, for the thermodynamic temperature T of the gas. [1]
(ii) Show that the mean translational kinetic energy \(E_K\) of a molecule of the gas is given by
\(E_{k}=\frac{3}{2}kT\) [2]
(iii) Explain why the internal energy of the gas is equal to the total kinetic energy of the molecules. [2]
(c) The gas in (b) is supplied with thermal energy Q.
(i) Explain, with reference to the first law of thermodynamics, why the increase in internal energy of the gas is Q. [2]
(ii) Use the expression in (b)(ii) and the information in (c)(i) to show that the specific heat capacity c of the gas is given by
\(c=\frac{3k}{2m}\) [2]
(d) The container in (b) is now replaced with one that does not have a fixed volume. Instead, the gas is able to expand, so that the pressure of the gas remains constant as thermal energy is supplied. Suggest, with a reason, how the specific heat capacity of the gas would now compare with the value in (c)(ii). [2] [Total: 13]
Answer/Explanation
Ans
(a) (thermal) energy per unit mass (to cause temperature change)
(thermal) energy per unit change in temperature B1
(b) (i) (T =) pV / Nk
(b) (ii) (pV =) NkT = ⅓Nm < c2>
or
pV = NkT and pV = ⅓Nm < c2>
leading to ½ m <c2> = (3/2)kT and ½ m <c2> = EK
(b) (iii) internal energy = Σ EK (of molecules) + Σ EP (of molecules)
or
no forces between molecules
potential energy of molecules is zero
(c) (i) increase in internal energy = Q + work done
constant volume so no work done
(c) (ii) c = Q / Nm ΔT
= [N × (3/2)kΔT] / (NmΔT) = 3k /2m
(d) (as it expands) gas does work (against the atmosphere/external pressure) B1