Question
A jet of water hits a vertical wall at right angles, as shown in Fig. 3.1.
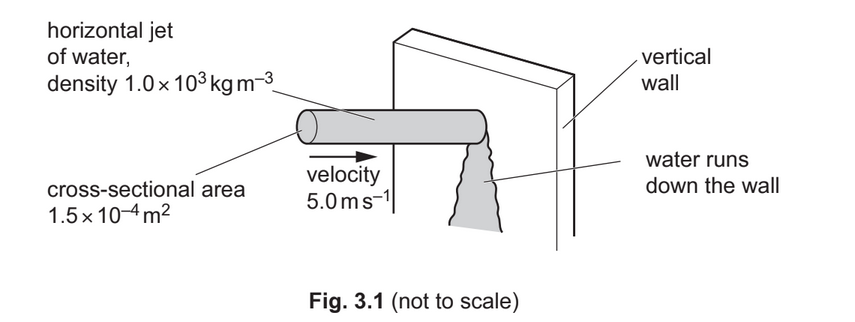
The water hits the vertical wall with a velocity of 5.0m/s in a horizontal direction. The cross-sectional area of the jet is \(1.5 \times 10^{–4}m^2\). The density of the water is \(1.0 \times 10^3 kg m^{–3}\).
The water runs down the wall after hitting it.
(a) Show that, over a time of 1.6s, the mass of water hitting the wall is 1.2kg.
[2]
(b) Calculate:
(i) the decrease in the horizontal momentum of the mass of water in (a) due to hitting the wall
decrease in momentum = ……………………………………………. Ns [1]
(ii) the magnitude of the horizontal force exerted on the water by the wall.
force = ……………………………………………… N [1]
(c) State and explain the magnitude of the horizontal force exerted on the wall by the water.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(d) Calculate the pressure exerted on the wall by the water.
pressure = ……………………………………………. Pa [2]
[Total: 7]
Answer/Explanation
Ans:
(a) \((m =) \rho V\)
\(= 1.0 \times 10^3 \times 1.5 x 10^{-4} \times 5.0 \times 1.6 = 1.2 (kg)\)
(b)(i) \((\Delta )p = 1.2 \times 5.0\)
\(= 6.0 N s\)
(b)(ii) F = 6.0/1.6 or \(1.2 \times 5.0/1.6\)
= 3.8 N
(c) Newton’s third law applies (so) 3.8 N.
(d) p = F/A
\(= 3.8/1.5 \times 10^{-4}\)
\(= 2.5 \times 10^4 \)Pa
Question
A person uses a trolley to move suitcases at an airport. The total mass of the trolley and suitcases is 72kg.
(a) The person pushes the trolley and suitcases along a horizontal surface with a constant speed of 1.4 m/s and then releases the trolley. The released trolley moves in a straight line and comes to rest. Assume that a constant total resistive force of 18N opposes the motion of the trolley and suitcases.
(i) Calculate the power required to overcome the total resistive force on the trolley and suitcases when they move with a constant speed of 1.4ms–1.
power = …………………………………………….. W
(ii) Calculate the time taken for the trolley to come to rest after it is released.
time = ……………………………………………… s
(b) At another place in the airport, the trolley and suitcases are on a slope, as shown in Fig. 2.1.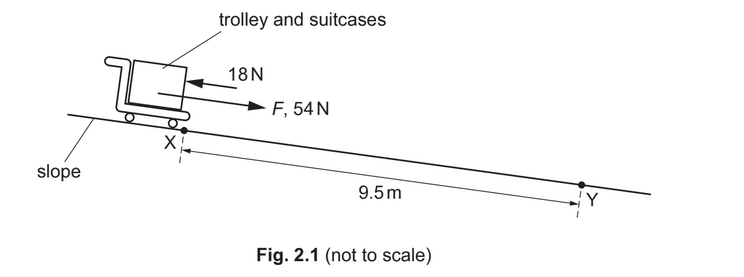
The person releases the trolley from rest at point X. The trolley moves down the slope in a straight line towards point Y. The distance along the slope between points X and Y is 9.5m. The component F of the weight of the trolley and suitcases that acts along the slope is 54N. Assume that a constant total resistive force of 18N opposes the motion of the trolley and suitcases.
(i) Calculate the speed of the trolley at point Y.
speed = ………………………………………… ms–1
(ii) Calculate the work done by F for the movement of the trolley from X to Y.
work done = ……………………………………………… J
(iii) The trolley is released at point X at time t = 0.
On Fig. 2.2, sketch a graph to show the variation with time t of the work done by F for the
movement of the trolley from X to Y.
Numerical values of the work done and t are not required.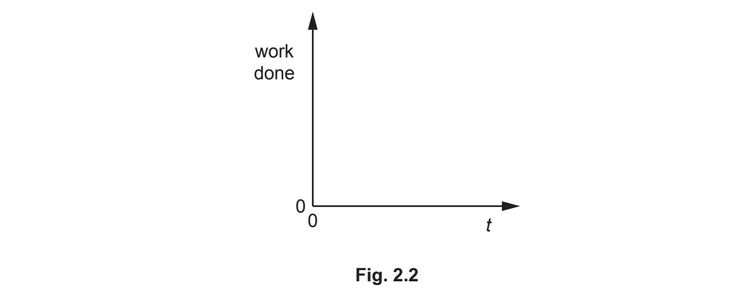
(c) The angle of the slope in (b) is constant. The frictional forces acting on the wheels of the moving trolley are also constant.
Explain why, in practice, it is incorrect to assume that the total resistive force opposing the motion of the trolley and suitcases is constant as the trolley moves between X and Y.
………………………………………………………………………………………….. [1]
Answer/Explanation
Ans:
(a)(i) P = Fv
= 18× 1.4
= 25W
(a)(ii) a =F / m
a = 18 / 72 = 0.25 \((m s^{–2})\)
t = 1.4 / 0.25 = 5.6 s
(b)(i) a = (54– 18) / 72 or 36 / 72 (= 0.50 \(m s^{–2})\)
\(v^2\) = 2× 0.50× 9.5
v = 3.1 \(m s^{–1}\)
(b)(ii) W = 54 × 9.5
= 510 J
(b)(iii) curved line from the origin
gradient of line increases
(c) (force due to) air resistance increases/changes/not constant or air resistance increases with speed