Question
A small charged glass bead of weight \(5.4 × 10^{–5}\) N is initially at rest at point A in a vacuum. The bead then falls through a uniform horizontal electric field as it moves in a straight line to point B, as illustrated in Fig. 2.1.
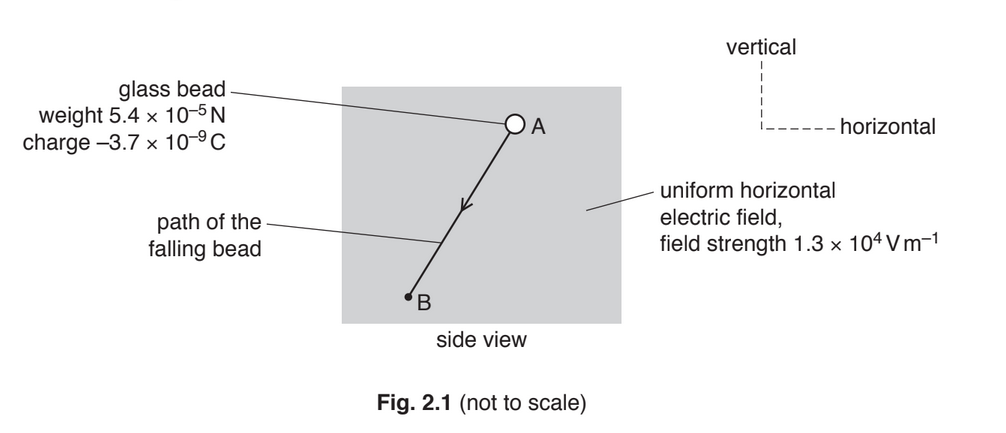
The electric field strength is \(1.3 × 10^4Vm^{–1}\). The charge on the bead is \(–3.7 × 10^{–9}\)C.
(a) Describe how two metal plates could be used to produce the electric field. Numerical values are not required.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(b) Determine the magnitude of the electric force acting on the bead.
electric force = …………………………………………….. N [2]
(c) Use your answer in (b) and the weight of the bead to show that the resultant force acting on it is \(7.2 × 10^{–5}\) N. [1]
(d) Explain why the resultant force on the bead of \(7.2 × 10^{–5}\) N is constant as the bead moves along path AB.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(e) (i) Calculate the magnitude of the acceleration of the bead along the path AB.
acceleration = ………………………………………… \(ms^{–2}\) [2]
(ii) The path AB has length 0.58m.
Use your answer in (i) to determine the speed of the bead at point B.
speed = ………………………………………… \(ms^{–1}\) [2] [Total: 11]
Answer/Explanation
Ans:
(a) the (two) plates are vertical (and separated)
left plate positively charged and right plate negatively charged/earthed
or
right plate negatively charged and left plate positively charged/earthed
(b) \(F = Eq \)
\(= 1.3× 104 × 3.7× 10^{–9}\)
\(= 4.8× 10^{–5}\) N
(c) 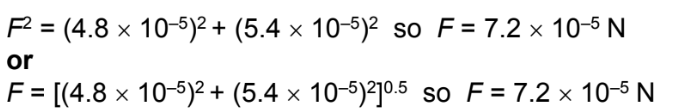
(d) electric force is constant (because field strength/ E is constant)
weight is constant (and so resultant force constant)
(e)(i) \(m = 5.4× 10^{–5} / 9.81 (= 5.5× 10^{–6})\)
\(a = 7.2× 10^{–5} / (5.5 × 10^{–6})=13m s^{–2}\)
(e)(ii) \(v^2 =u^2 + 2as\)
\( v^2 = 2× 13× 0.58\)
\(v = 3.9m/s\)
Question
An electron is travelling in a straight line through a vacuum with a constant speed of 1.5 × 107ms–1.
The electron enters a uniform electric field at point A, as shown in Fig. 5.1.
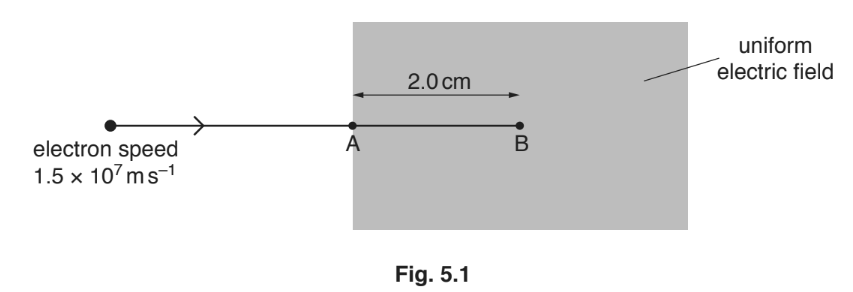
The electron continues to move in the same direction until it is brought to rest by the electric field at point B. Distance AB is 2.0cm.
(a) State the direction of the electric field.
![]()
(b) Calculate the magnitude of the deceleration of the electron in the field.
deceleration = …………………………………………..ms–2 [2]
(c) Calculate the electric field strength.
electric field strength = ………………………………………….Vm–1 [3]
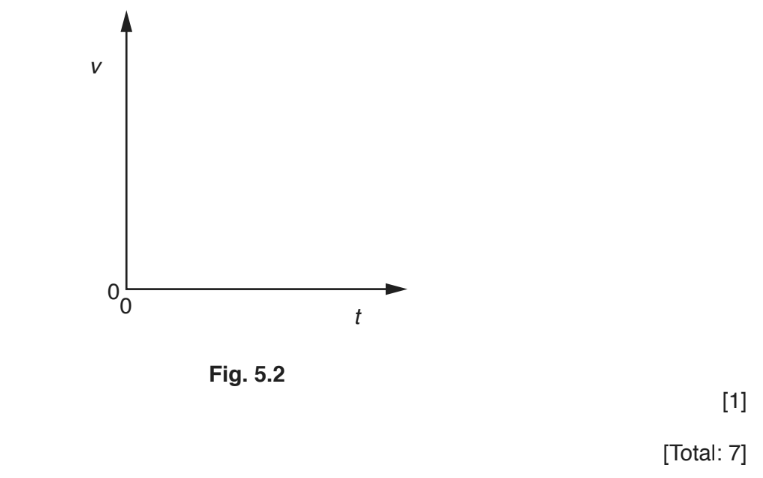
(d) The electron is at point A at time t = 0.
On Fig. 5.2, sketch the variation with time t of the velocity v of the electron until it reaches point B. Numerical values of v and t do not need to be shown.
Answer/Explanation
Ans:
(a) to the right /from the left /from A to B/ in the same direction as electron velocity
(b) \(v^ 2 = u^ 2 + 2as\)
a = (1.5 × 107)2 /(2 × 2.0 × 10–2)
Other alternative calculations:
e.g. a = 1.5×107/ 2.67×10–9
e.g. a = [(1.5×107 × 2.67×10–9) – 2.0×10–2] × [2 /(2.67×10–9)2]
e.g. a = (2.0×10–2 × 2)/(2.67×10–9)2
= 5.6 × 1015 m s–2
(c) E = F/Q
= (9.1 × 10–31 × 5.6 × 1015)/ 1.6 × 10–19
= 3.2 ×104 Vm–1
(d) straight line with negative gradient starting at an intercept on the v-axis and ending at an intercept on the t-axis.