Question
A rigid sphere is held at rest on the sea bed. When the sphere is released, it rises to the surface of the sea. The seawater has a uniform density.
Which statement about the sphere, from its release until it reaches the surface, is correct?
A The sphere always moves with constant acceleration.
B The sphere always moves with constant velocity.
C The upthrust on the sphere always decreases.
D The upthrust on the sphere is always constant.
Answer/Explanation
Ans: D
The upthrust on the sphere is given as,
\( F_B = \rho g V\)
Question
What is a unit for density?
A \(N m^{–3}\) B \(g mm^{–1}\) C \(kg\, cm^{–2}\) D \(\mu g\, mm^{–3}\)
Answer/Explanation
Ans: D
The density is given as,
\(\rho = \frac{M}{V}\)
The unit of the density is therefore given as,
\([\rho] =\frac{kg }{m^3}\)
\( = \frac{10^9 \mu g }{ 10^9 mm^3}\)
Question
A uniform solid block is fully submerged in a tank of water. The dimensions of the block are x and y, as shown.
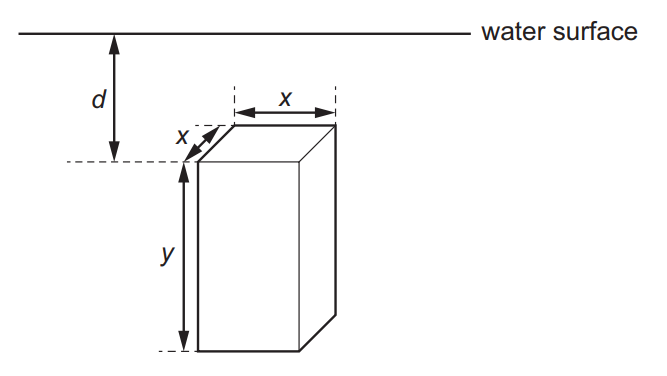
The block is held vertically in the position shown. The density of the block is the same as the density of the water. If the block is always held at the same depth d below the surface of the water, which single change would increase the magnitude of the upthrust force on the block?
A decrease the density of the block
B hold the block horizontally
C increase dimension y
D increase the density of the block
Answer/Explanation
Ans:C
The upthrust on the block is given as,
\(F_B = \rho g V\)
where \(\rho, g, V\) are the density of the water, acceleration due to gravity and the volume of the block.
Hence the upthrust will not be affected by the decrease in the density of the block, hence the option (A) is wrong.
The upthrust is independent of the orientation of the block, hence the option (B) is wrong.
The upthrust will increase if we increase y, hence the option (C) is correct.
The upthrust does not depend on the density of the block, hence the option (D) is incorrect.
Hence the option (C) is correct.
Question
A bird dives to a depth of 1.50 m below the surface of a lake. Atmospheric pressure is 101 kPa. The density of water is 1000 kgm–3.
What is the pressure at this depth?
A 14.7 kPa B 86.3 kPa C 103 kPa D 116 kPa
Answer/Explanation
Ans:D
The pressure at the depth is given as,
\(P = P_0 + \rho g h\)
\( P = 101 000 + 1000\times 9.8\times 1.5 = 116000 Pa = 116 kPa \)
Question
Water of depth 9.0 cm is covered by oil of depth 5.0 cm in a measuring cylinder.
The density of the water is 1000 kg m-3 and the density of the oil is 800 kgm-3.
What is the total pressure exerted on the base of the measuring cylinder due to the oil and water?
A 390Pa B 880Pa C 1200Pa D 1300Pa
Answer/Explanation
Ans: D
The total pressure at the base of the cylinder is given as,
\( P = \rho_w gh_w + \rho_ogh_o\)
\(P = 1000\times 9.8\times 0.09 + 800\times 9.8\times0.05 = 1300 Pa\)
Hence the option (D) is correct.