Question
(a) (i) State the conditions required for the formation of a stationary wave.
……………………………………………………………………………………………. [2]
(ii) State the phase difference between any two vibrating particles in a stationary wave between two adjacent nodes.
phase difference = ………………………………………………..° [1]
(b) A motorcycle is travelling at 13.0 m/s along a straight road. The rider of the motorcycle sees a pedestrian standing in the road directly ahead and operates a horn to emit a warning sound.
The pedestrian hears the warning sound from the horn at a frequency of 543Hz. The speed of the sound in the air is 334 m/s.
(i) Calculate the frequency, to three significant figures, of the sound emitted by the horn.
frequency = ……………………………………………. Hz [2]
(ii) The motorcycle rider passes the stationary pedestrian and then moves directly away from her. As the rider moves away, he operates the horn for a second time. The pedestrian now hears sound that is increasing in frequency.
State the variation, if any, in the speed of the motorcycle when the rider operates the horn for the second time…………………………………… [1]
(c) A beam of vertically polarised monochromatic light is incident normally on a polarising filter, as shown in Fig. 5.1.
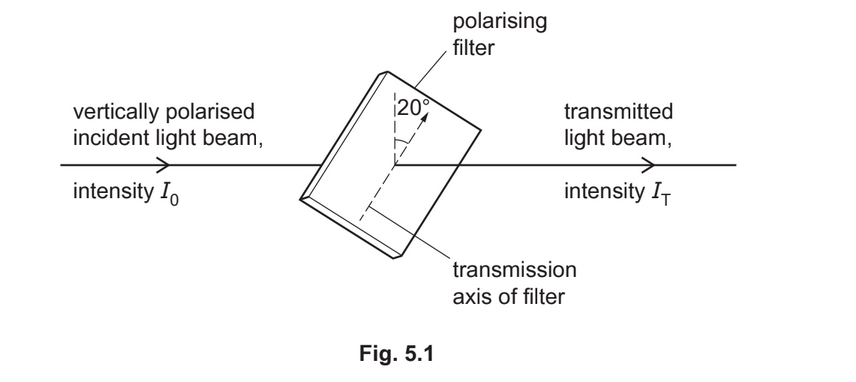
The filter is positioned with its transmission axis at an angle of 20° to the vertical. The incident light has intensity \(I_0\) and the transmitted light has intensity \(I_T\).
(i) By considering the ratio \(\frac{I_T}{I_0}\) calculate the ratio 
Show your working. ratio = ………………………………………………… [3]
(ii) The filter is now rotated, about the direction of the light beam, from its starting position shown in Fig. 5.1. The direction of rotation is such that the angle of the transmission axis to the vertical initially increases.
Calculate the minimum angle through which the filter must be rotated so that the intensity of the transmitted light returns to the value that it had when the filter was at its starting position.
angle = ………………………………………………. ° [1]
Answer/Explanation
Ans:
(a)(i) (two) waves travelling (at same speed) in opposite directions overlap waves (of the same type) have same frequency/wavelength
(a)(ii) phase difference = 0

Question
The variation with time t of the displacement y of a wave X, as it passes a point P, is shown in Fig. 5.1.
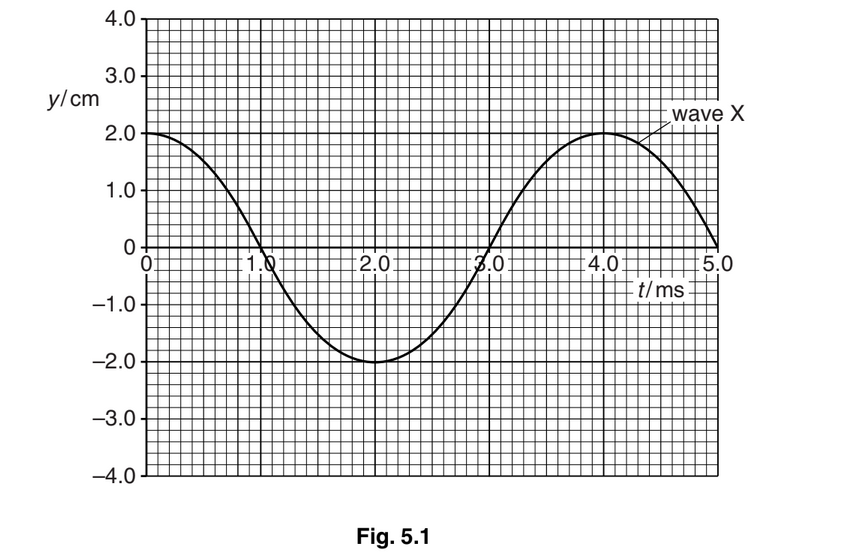
The intensity of wave X is I.
(a) Use Fig. 5.1 to determine the frequency of wave X.
frequency = ……………………………………………. Hz [2]
(b) A second wave Z with the same frequency as wave X also passes point P. Wave Z has intensity 2I. The phase difference between the two waves is 90°. On Fig. 5.1, sketch the variation with time t of the displacement y of wave Z.
Show your working.
(c) A double-slit interference experiment is used to determine the wavelength of light emitted
from a laser, as shown in Fig. 5.2.
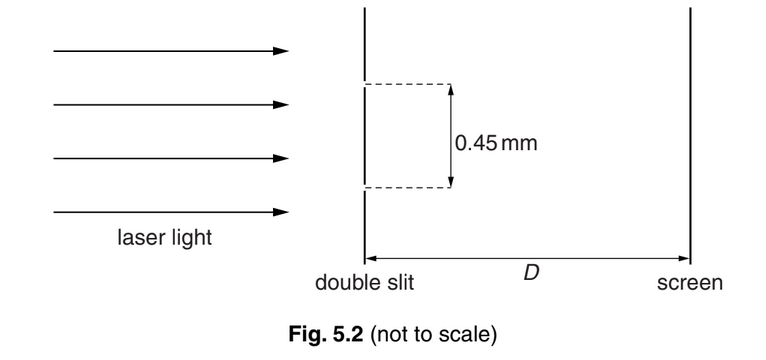
The separation of the slits is 0.45 mm. The fringes are viewed on a screen at a distance D from the double slit. The fringe width x is measured for different distances D. The variation with D of x is shown in Fig. 5.3.
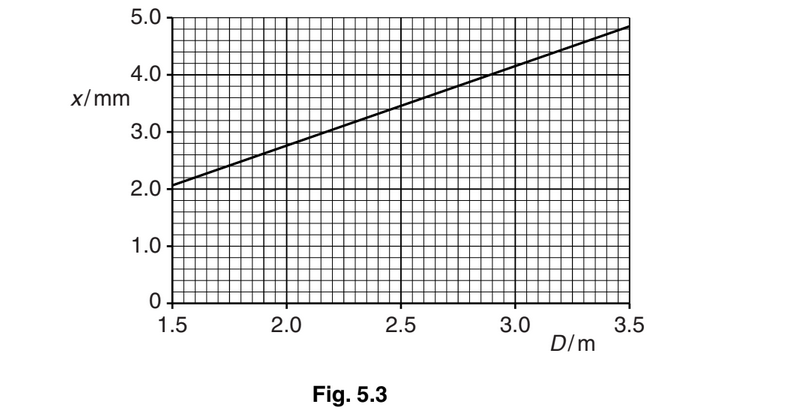
(i) Use the gradient of the line in Fig. 5.3 to determine the wavelength, in nm, of the laser light.
wavelength = ……………………………………………. nm [4]
(ii) The separation of the slits is increased. State and explain the effects, if any, on the graph of Fig. 5.3.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………[2] [Total: 11]
Answer/Explanation
(a) \(T = 4~(ms)~ or~ 4 × 10^{–3}\) (s)
f = 1/T = 1/0.004
= 250Hz
(b) intensity ∝ \((amplitude)^2\) and amplitude = 2.8 (2.83)(cm)
curve with same period and with amplitude 2.8cm
curve shifted 1.0ms to left or to right of wave X
