Question
(a) For a progressive wave, state what is meant by wavelength.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [1]
(b) A light wave from a laser has a wavelength of 460nm in a vacuum.
Calculate the period of the wave.
period = ……………………………………………… s [3]
(c) The light from the laser is incident normally on a diffraction grating.
Describe the diffraction of the light waves at the grating.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(d) A diffraction grating is used with different wavelengths of visible light. The angle θ of the
fourth-order maximum from the zero-order (central) maximum is measured for each
wavelength. The variation with wavelength λ of sinθ is shown in Fig. 4.1.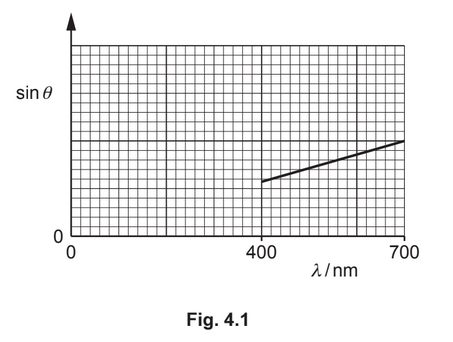
(i) The gradient of the graph is G.
Determine an expression, in terms of G, for the distance d between the centres of two
adjacent slits in the diffraction grating.
d = …………………………………………………
(ii) On Fig. 4.1, sketch a graph to show the results that would be obtained for the
second-order maxima.
Answer/Explanation
Ans:
(a) distance moved by wavefront/energy during one cycle/oscillation/period (of source)
or
minimum distance between two wavefronts
or
distance between two adjacent wavefronts
(b) v =λ / T
or
v = fλ and f = 1 / T
\(T = 460 \times 10^{–9} / 3.00 \times 10^8 \)
\(= 1.5\times 10^{–15} s\)
(c) waves pass through/enter the slit(s)
waves spread (into geometric shadow) B1
(d)(i) n λ = d sin θ
G = sin θ / λ
d = 4 / G
(d)(ii) straight line from 400 nm to 700 nm that is always below printed line
straight line has smaller gradient than printed line and is 5 small squares high at wavelength of 700 nm
Question
(a) For a progressive wave, state what is meant by:
(i) the wavelength
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(ii) the amplitude.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(b) A beam of red laser light is incident normally on a diffraction grating.
(i) Diffraction of the light waves occurs at each slit of the grating. The light waves emerging from the slits are coherent.
Explain what is meant by:
1. diffraction
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
2. coherent.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
(ii) The wavelength of the laser light is 650nm. The angle between the third order diffraction maxima is 68°, as illustrated in Fig. 4.1.
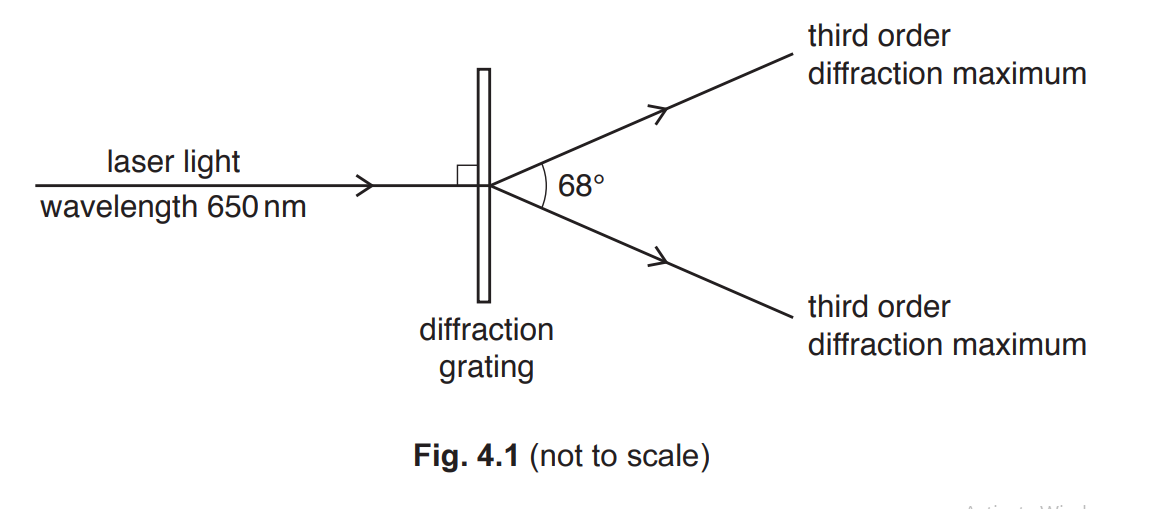
Calculate the separation d between the centres of adjacent slits of the grating.
d = …………………………………………….. m
(iii) The red laser light is replaced with blue laser light.
State and explain the change, if any, to the angle between the third order diffraction maxima.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
Answer/Explanation
(a)(i)
distance moved by wavefront / energy during one cycle / vibration / oscillation / period (of source)
or
minimum distance between two wavefronts
or
distance between two adjacent wavefronts
(a)(ii)
maximum displacement (of particle / point on wave)
(b)(i)
1 light / waves spread (at each slit)
2 constant phase difference (between light / waves)
(b)(ii)
n λ = d sin θ
d = 3 × 650 × 10–9 / sin34°
d = 3.5 × 10–6 m
(b)(iii)
wavelength of blue light is shorter (than 650 nm / red light)
so angle (between third order diffraction maxima) decreases