Question
The ends of a metal resistance wire are connected to a battery of electromotive force (e.m.f.) 8.0V and negligible internal resistance, as shown in Fig. 6.1.
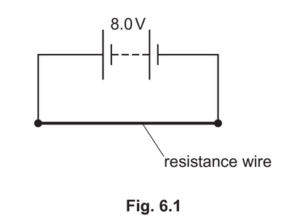
The power dissipated by the resistance wire is 36W.
(a) Calculate:
(i) the current in the resistance wire
current = ……………………………………………….A [2]
(ii) the number of free electrons that pass through the resistance wire in a time of 50s
number = ………………………………………………… [2]
(iii) the resistance of the wire.
resistance = ……………………………………………… Ω [2]
(b) The metal of the resistance wire in the circuit has a resistivity of \(1.4 \times 10–^{6}\) Ω-m. The cross-sectional area of the wire is 0.25 \(mm^2\).
Determine the length of the wire.
length = ………………………………………………m [2]
(c) The circuit shown in Fig. 6.1 is modified by replacing the original resistance wire with a second resistance wire. The second wire has a greater diameter than the original wire. There are no other differences between the second wire and the original wire. By reference to resistance, state and explain whether the power dissipated by the second wire is more than, less than or the same as the power dissipated by the original wire.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
(d) The circuit shown in Fig. 6.1 is modified by connecting a second battery, of e.m.f. 8.0V and negligible internal resistance, in parallel with the original battery and the original resistance wire, as shown in Fig. 6.2.
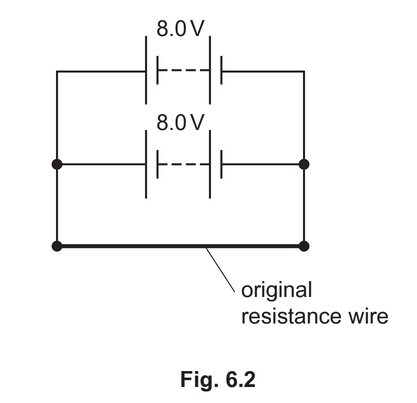
By reference to the current in the resistance wire, state and explain whether the addition of the second battery causes the power in the original resistance wire to decrease, increase or stay the same.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………… [2]
[Total: 12]
Answer/Explanation
Ans:
(a)(i)
\(P =VI\)
\(I = 36 / 8.0 = 4.5A\)
(a)(ii) charge = 4.5× 50 = 225
number \(= 225 / 1.6 × 10^{–19}\)
\(= 1.4 × 10^{21}\)
(b) \(R = ρL / A\)
\(L = (1.8 × 0.25 × 10^{–6}) / 1.4 × 10^{–6} = 0.32 m\)
(c) (larger cross-sectional area, same length, same resistivity and so) less resistance (same p.d. and more current so) more power (dissipated)
(d) current (in wire) is the same (same p.d. across wire so) power stays the same
Question
(a) State Kirchhoff’s second law.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) A battery has electromotive force (e.m.f.) 4.0V and internal resistance 0.35Ω. The battery is
connected to a uniform resistance wire XY and a fixed resistor of resistance R, as shown in
Fig. 5.1.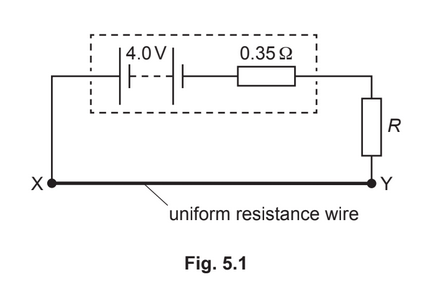
Wire XY has resistance 0.90Ω. The potential difference across wire XY is 1.8V.
Calculate:
(i) the current in wire XY
current = ……………………………………………… A [1]
(ii) the number of free electrons that pass a point in the battery in a time of 45s
number = …………………………………………………
(iii) resistance R.
R = …………………………………………….. Ω
(c) A cell of e.m.f. 1.2V is connected to the circuit in (b), as shown in Fig. 5.2.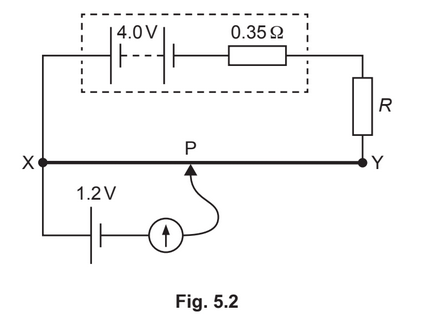
The connection P is moved along the wire XY. The galvanometer reading is zero when
distance XP is 0.30m.
(i) Calculate the total length L of wire XY.
L = …………………………………………….. m [2]
(ii) The fixed resistor is replaced by a different fixed resistor of resistance greater than R.
State and explain the change, if any, that must be made to the position of P on wire XY
so that the galvanometer reading is zero.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
Answer/Explanation
Ans:
(a) sum of e.m.f.(s) = sum of p.d.(s)
or
(algebraic) sum of e.m.f.(s) and p.d.(s) is zero
around a loop/around a closed circuit
(b)(i) I = 1.8 / 0.90= 2.0A
(b)(ii) Q =It
number \(= (2.0\times 45) / 1.60\times 10^{–19}= 5.6 \times 10^{20}\)
(b)(iii) 4.0 = 1.8 + [2.0× (0.35 +R)]
or
4.0 = 2.0× (0.90 + 0.35 +R)
R = 0.75Ω
(c)(i) 1.2 / 1.8 = 0.30 / L
L = 0.45 m
(c)(ii) p.d. across XY decreases/p.d. across XP decreases
(so) P is moved towards Y/away from X/to the right