![]()
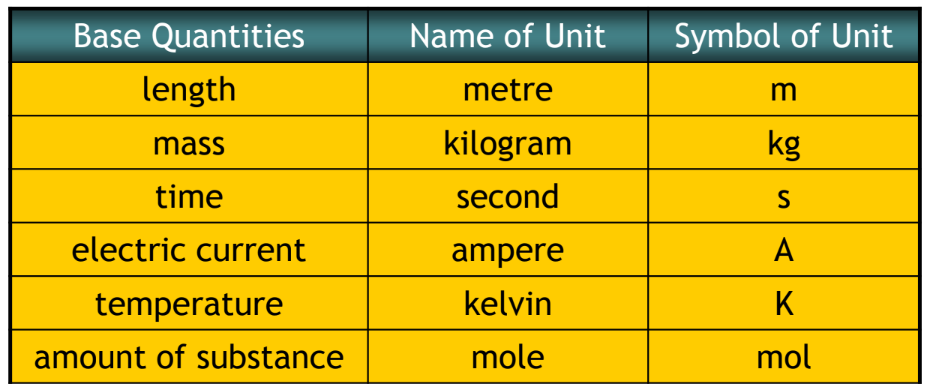
| • Base quantities are the quantities on the basis of which other quantities are expressed. | • The quantities that are expressed in terms of base quantities are called derived quantities |
![]()
- SI Units – International System of Units
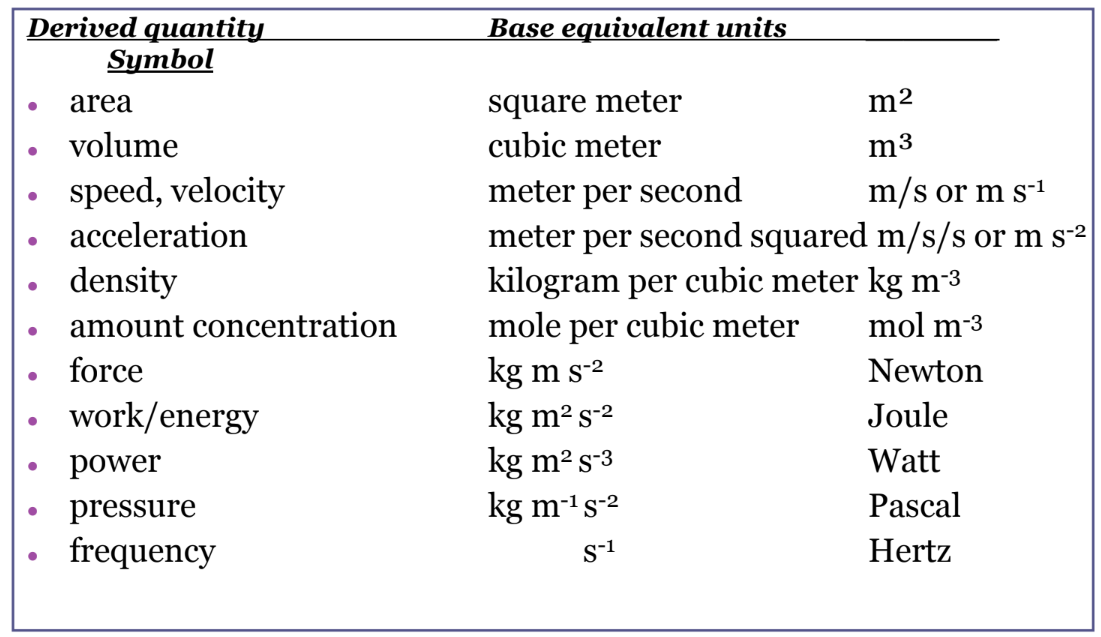
Derived quantity & equations
- A derived quantity has an equation which links to other quantities.
- It enables us to express a derived unit in terms of base-unit equivalent.
Example: $\mathrm{F}=\mathrm{ma} ;$ Newton $=\mathrm{kg} \mathrm{m} \mathrm{s}{ }^{-2}$
$
\mathrm{P}=\mathrm{F} / \mathrm{A} ; \quad \text { Pascal }=\mathrm{kg} \mathrm{m} \mathrm{s} \mathrm{m}^{-2} / \mathrm{m}^2=\mathrm{kg} \mathrm{m}^{-1} \mathrm{~s}^{-2}
$
Some derived units
SI Units
1. Equation: area $=$ length $\times$ width
In terms of base units: Units of area $=\mathrm{m} \times \mathrm{m}=\mathrm{m}^2$
2. Equation: volume $=$ length $\times$ width $\times$ height
In terms of base units: Units of volume $=\mathrm{m} \times \mathrm{m} \times \mathrm{m}=\mathrm{m}^3$
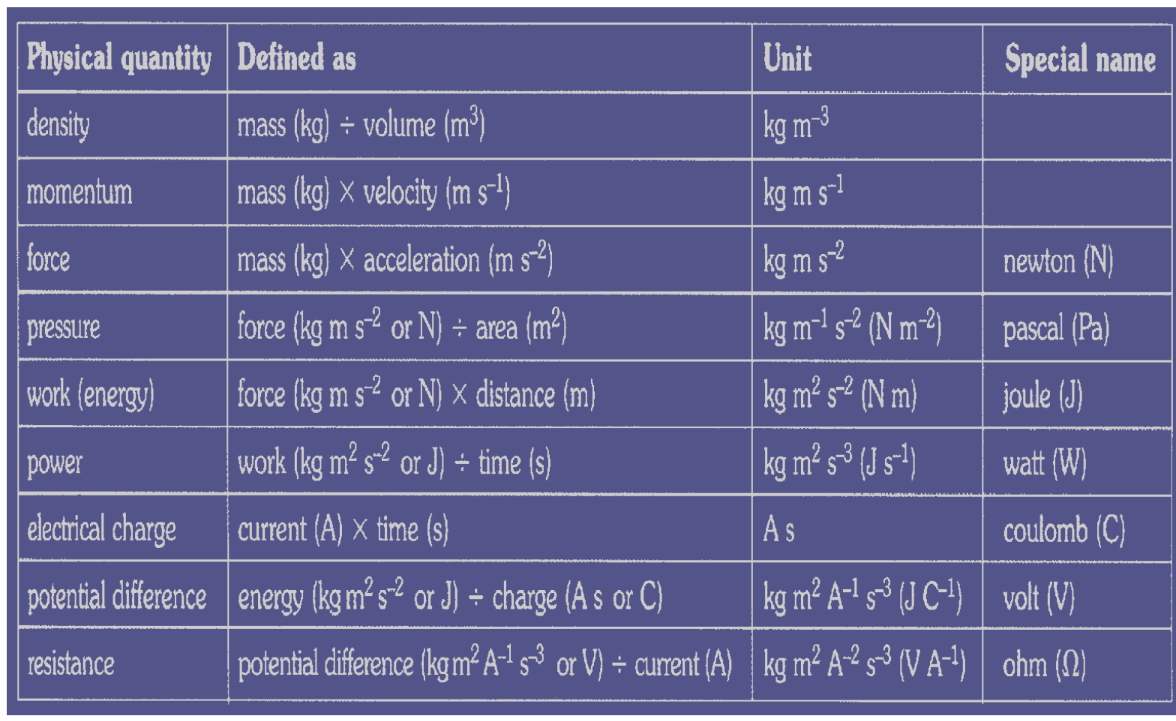
3. Equation: density $=$ mass $\div$ volume
In terms of base units: Units of density $=\mathrm{kg} \mathrm{m}^{-3}$
- Work out the derived quantities for:
1. Equation: $\quad$ speed $=\frac{\text { distance }}{\text { time }}$
In terms of base units: Units of speed $=\mathrm{ms}^{-1}$
2. Equation: $\quad$ acceleration $=\frac{\text { velocity }}{\text { time }}$
In terms of base units: Units of acceleration $=\mathrm{ms}^{-2}$
3. Equation: force $=$ mass $\times$ acceleration
In terms of base units: Units of force $=\mathrm{kg} \mathrm{ms}^{-2}$
- Work out the derived quantities for:
1. Equation: $\quad$ Pressure $=\frac{\text { Force }}{\text { Area }}$
In terms of base units: Units of pressure $=\mathrm{Kgm}^{-1} \mathrm{~s}^{-2}$
2. Equation: Work $=$ Force $\times$ Displacement
In terms of base units: Units of work $=\mathrm{Kgm}^2 \mathrm{~S}^{-2}$
3. Equation: Power $=\frac{\text { Workdone }}{\text { Time }}$
In terms of units: Units of power $=\quad \mathrm{Kgm}^2 \mathrm{~s}^{-3}$
SI Units – Fill in…
For you to know…
Key Concept
1. A physical quantity is a quantity that can be measured and consists of a numerical magnitude and a unit.
2. The physical quantities can be classified into base quantities and derived quantities.
3. There are seven base quantities: length, mass, time, current, temperature, amount of substance and luminous intensity.
4. The SI units for length, mass, time, temperature and amount of substance, electric current are metre, kilogram, second, kelvin, mole and ampere respectively.
Homogeneity of an equation
- An equation is homogeneous if quantities on BOTH sides of the equation has the same unit.
- E.g. $s=u t+1 / 2 a^2$
- LHS : unit of $s=m$
- RHS : unit of ut $=\mathbf{m s}^{-1} \mathrm{xS}_{\mathrm{x}}=\mathbf{m}$
- Unit on LHS = unit on RHS
- Hence equation is homogeneous
Non-homogeneous
- $\mathrm{P}=\rho g h^2$
- LHS ; unit of $\mathrm{P}=\mathrm{Nm}^{-2}=\mathrm{kgm}^{-1} \mathrm{~s}^{-2}$
- RHS : unit of $\rho \mathrm{gh}^2=\mathrm{kgm}^{-3}\left(\mathrm{~ms}^{-2}\right)\left(\mathrm{m}^2\right)=\mathrm{kgs}^{-2}$
- Unit on LHS $\neq$ unit on RHS
- Hence equation is not homogeneous
Homogeneity of an equation
- Note: numbers has no unit
- some constants have no unit.
- e.g. $\pi$
- A homogeneous eqn may not be physically correct but a physically correct eqn is definitely homogeneous
- E.g. $s=2 u t+a t^2$ (homogenous but not correct)
- $\quad \mathbf{F}=\mathbf{m a} \quad$ (homogeneous and correct)
Magnitude
- Prefix : magnitudes of physical quantity range from very large to very small.
- E.g. mass of sun is $10^{30} \mathrm{~kg}$ and mass of electron is $10^{-31} \mathbf{k g}$.
- Hence, prefix is used to describe these magnitudes.
Significant number
- Magnitudes of physical quantities are often quoted in terms of significant number.
- Can you tell how many sig. fig. in these numbers?
- 103, 100.0, 0.030, 0.4004, 200
- If you multiply 2.3 and 1.45, how many sf should you quote?
- 3.19, 3.335, 3.48
- 3.312, 3.335, $3 \cdot 358$