Significant number
- Magnitudes of physical quantities are often quoted in terms of significant number.
- Can you tell how many sig. fig. in these numbers?
- 103, 100.0, 0.030, 0.4004, 200
- If you multiply 2.3 and 1.45, how many sf should you quote?
- 3.19, 3.335, 3.48
- 3.312, 3.335, $3 \cdot 358$
The rules for identifying significant figures
- The rules for identifying significant figures when writing or interpreting numbers are as follows:-
- All non-zero digits are considered significant. For example, 91 has two significant figures ( 9 and 1 ), while 123.45 has five significant figures $(1,2,3,4$ and 5$)$.
- Zeros appearing anywhere between two non-zero digits are significant. Example: 101.1203 has seven significant figures: $1,0,1,1,2,0$ and 3.
- Leading zeros are not significant. For example, 0.00052 has two significant figures: 5 and 2.
The rules for identifying significant figures (cont)
- Trailing zeros in a number containing a decimal point are significant. For example, 12.2300 has six significant figures: $1,2,2,3,0$ and 0 . The number 0.000122300 still has only six significant figures (the zeros before the 1 are not significant). In addition, 120.00 has five significant figures since it has three trailing zeros.
- Often you will be asked to estimate some magnitudes of physical quantities around you.
- E.g. estimate the height of the ceiling, volume of an apple, mass of an apple, diameter of a strand of hair,
Estimates of physical quantities
• When making an estimate, it is only reasonable to give the figure to 1 or at most 2 significant figures since an estimate is not very precise.
$\begin{array}{cc}\text { Physical Quantity } & \text { Reasonable Estimate } \\ \text { Mass of } 3 \text { cans }(330 \mathrm{ml}) \text { of } & 1 \mathrm{~kg} \\ \text { Pepsi } & 1000 \mathrm{~kg} \\ \text { Mass of a medium-sized car } & 100 \mathrm{~m} \\ \text { Length of a football field } & 0.2 \mathrm{~s}\end{array}$
- Occasionally, students are asked to estimate the area under a graph. The usual method of counting squares within the enclosed area is used.
Convention for labelling tables and graphs
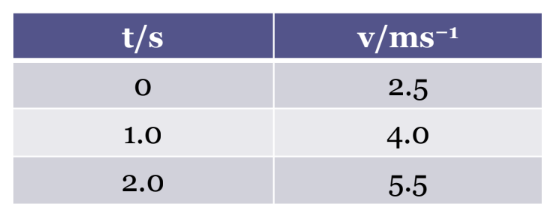

• The symbol / unit is indicated at the italics as indicated in the data column left.
• Then fill in the data with pure numbers.
• Then plot the graph after labelling x axis and y axis
[Illustration with sample graph on left]
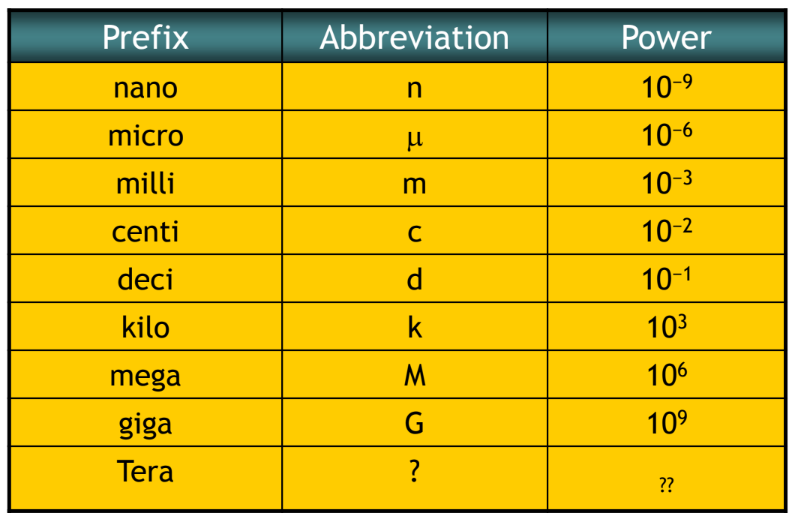
Prefixes
- For very large or very small numbers, we can use standard prefixes with the base units.
- The main prefixes that you need to know are shown in the table. (next slide)
Prefixes
- Prefixes simplify the writing of very large or very small quantities
Prefixes
- Alternative writing method
- Using standard form
- $N \times 10^n$ where $1 \leq N<10$ and $n$ is an integer

This galaxy is about $2.5 \times 10^6$ light years from the Earth. The diameter of this atom is about $1 \times 10^{-10} \mathrm{~m}$.