Newton’s laws of Motion
• Newton’s laws of motion are three physical laws which provide relationships between the forces acting on a body and the motion of the body.
Newton’s Laws: Force and Motion
• The First Law: Force and Inertia
• The Second Law: Force, Mass and Acceleration
• The Third Law: Action and Reaction
Newton’s first law

An object at rest tends to stay at rest and object in motion tends to stay in motion unless acted upon by an external force.
What does this mean ?
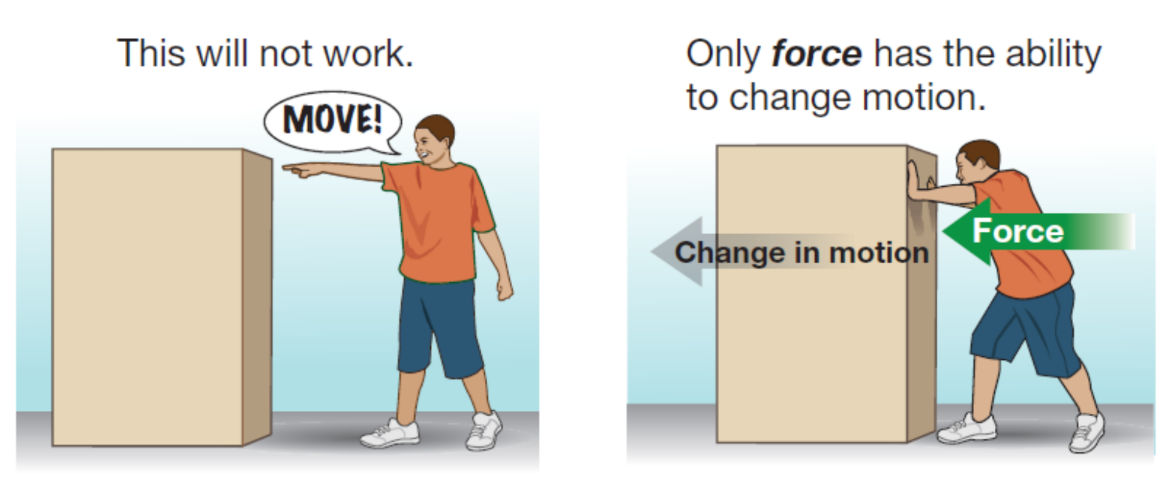
Basically, an object will keep doing what it was doing, unless acted on by an external force. If the object was sitting still, it will remain stationary. If it was moving at a constant velocity, it will keep moving at a constant velocity. It takes force to change the motion of an object.
The definition of force
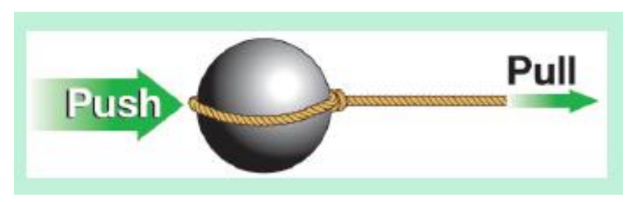
• The simplest concept of force is a push or a pull.
• In other words, force is the action that has the ability to create or change motion.
Force
• Force is an action that can change motion.
– A force is what we call a push or a pull, or any action that has the ability to change an object’s motion.
– Forces can be used to increase the speed of an object, decrease the speed of an object, or change the direction in which an object is moving.

– Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion.
Force
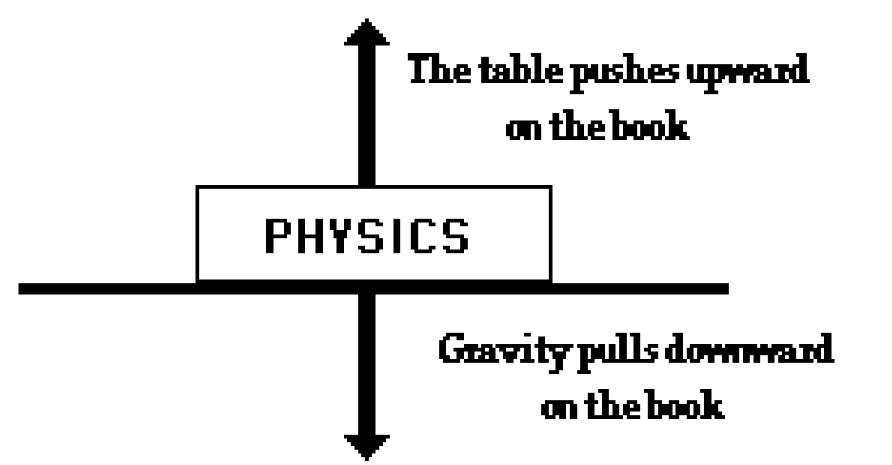
Balanced force
The forces on the book are balanced.
Balanced & Unbalanced
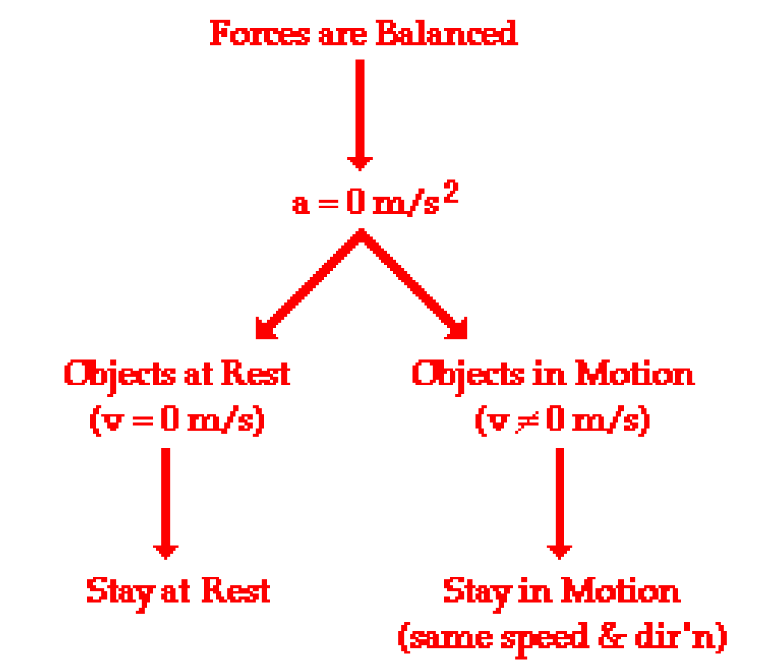
- If the forces on an object are equal and opposite or if the total force is zero they are said to be balanced, and the object experiences no change in motion.
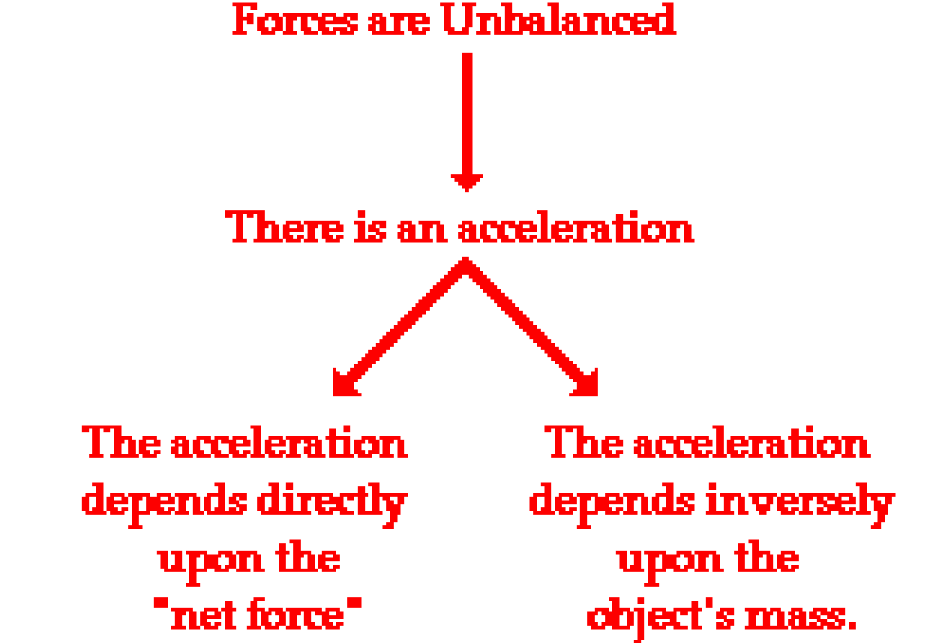
- If they are not equal and opposite or if the total forces is not zero, then the forces are unbalanced and the motion of the object changes.
These are some examples from real life

A soccer ball is sitting at rest. It takes an unbalanced force of a kick to change its motion.
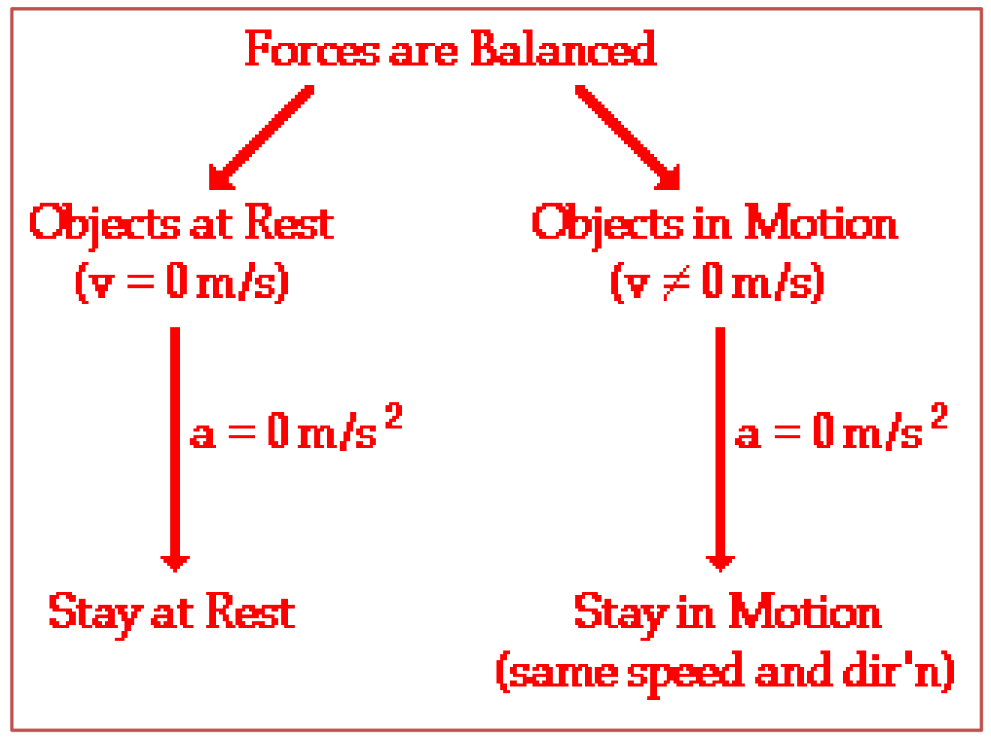
Newton’s First Law Applied to Rocket Liftoff
“Every object persists in its state of rest or uniform motion in a straight line unless it is compelled to change that state by forces impressed on it.”
Before firing:
Object in state of rest, airspeed zero.
Engine fired:
Thrust increases from zero.
Weight decreases slightly as fuel bums.
When Thrust is greater than Weight:
Net force (Thrust – Weight) is positive upward. Rocket accelerates upward Velocity increases
Newton’s First Law is also called the Law of Inertia
Inertia: the tendency of an object to resist changes in its state of motion
The First Law states that all objects have inertia. The more mass an object has, the more inertia it has (and the harder it is to change its motion).
Inertia
• Inertia is a term used to measure the ability of an object to resist a change in its state of motion.
• An object with a lot of inertia takes a lot of force to start or stop; an object with a small amount of inertia requires a small amount of force to start or stop.
• The word “inertia” comes from the Latin word inertus, which can be translated to mean “lazy.”
Examples from Real Life
A powerful locomotive begins to pull a long line of boxcars that were sitting at rest. Since the boxcars are so massive, they have a great deal of inertia and it takes a large force to change their motion. Once they are moving, it takes a large force to stop them.

If objects in motion tend to stay in motion, why don’t moving objects keep moving forever?
Things don’t keep moving forever because there’s almost always an unbalanced force acting upon it.
Example : A book sliding across a table slows down and stops because of the force of friction.

Forces Don’t Keep Objects Moving
Newton’s first law of motion declares that a force is not needed to keep an object in Motion.
For example : Slide a book across a table and watch it slide to a rest position. The book in motion on the table top does not come to a rest position because of the absence of a force; rather it is the presence of a force – that force being the force of friction – that brings the book to a rest position.
In the absence of a force of friction, the book would continue in motion with the same speed and direction – forever! (Or at least to the end of the table top.
If you throw a ball upwards it will eventually slow down and fall because of the force of gravity.

How do these systems in a car overcome the law of inertia?
• The engine
– supplies force that allows you to change motion by pressing the pedal.
• The brake system
– is designed to help you change your motion by slowing down.
• The steering wheel and steering system
– is designed to help you change your motion by changing your direction.
There are many more applications of Newton’s first law of motion. Several applications are listed below. Perhaps you could think about the law of inertia and provide explanations for each application.
- Blood rushes from your head to your feet while quickly stopping when riding on a descending elevator.
- The head of a hammer can be tightened onto the wooden handle by banging the bottom of the handle against a hard surface.
- To dislodge ketchup from the bottom of a ketchup bottle, it is often turned upside down and thrusted downward at high speeds and then abruptly halted.
- While riding a skateboard (or wagon or bicycle), you fly forward off the board when hitting a curb or rock or other object that abruptly halts the motion of the skateboard.
Check your understanding !
Question 1
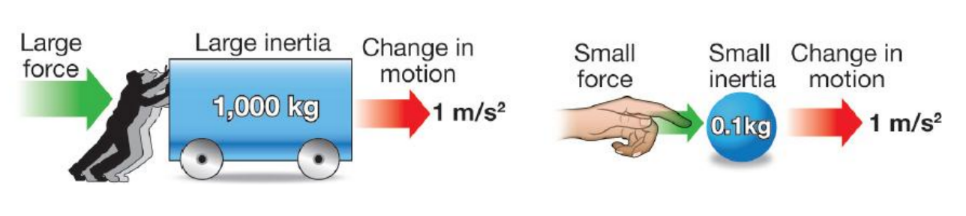
• Luke drops an approximately 5.0 kg fat cat (weight = 50.0 N) off the roof of his house into the swimming pool below. Upon encountering the pool, the cat encounters a 50.0 N upward resistance force (assumed to be constant).
a) Which one of the velocity-time graphs best describes the motion of the cat? Support your answer with sound reasoning.
Answer
• Graph B is correct. The cat first accelerates with a negative (downward) acceleration until it hits the water. Upon hitting the water, the cat experiences a balance of forces (50 N downwards due to gravity and 50 N upwards due to the water).
• Thus, the cat will finish its motion moving with a constant velocity. Graph B depicts both the initial negative acceleration and the final constant velocity.
Newton’s Second Law
Newton’s second law of motion…..
Force equals mass times acceleration
$
F=m a
$
Acceleration: a measurement of how quickly an object is changing speed.
From 1
st law…
when forces are balanced…..
When forces are unbalanced…
What does $\boldsymbol{F}=\boldsymbol{m} \boldsymbol{a}$ mean?
Force is directly proportional to mass and acceleration.
Imagine a ball of a certain mass moving at a certain acceleration. This ball has a certain force.
- Now imagine we make the ball twice as big (double the mass) but keep the acceleration constant. $\mathrm{F}=$ ma says that this new ball has twice the force of the old ball.
- Now imagine the original ball moving at twice the original acceleration. $\mathrm{F}=$ ma says that the ball will again have twice the force of the ball at the original acceleration.
Newton’s Second Law
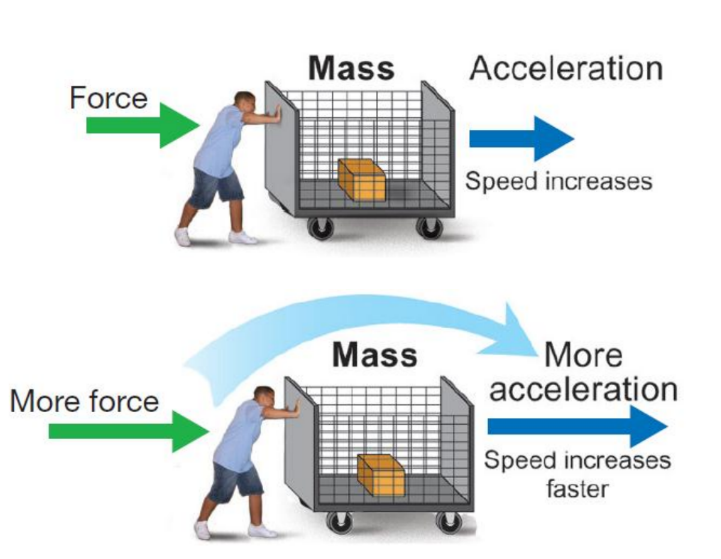
• If you apply more force to an object, it accelerates at a higher rate.
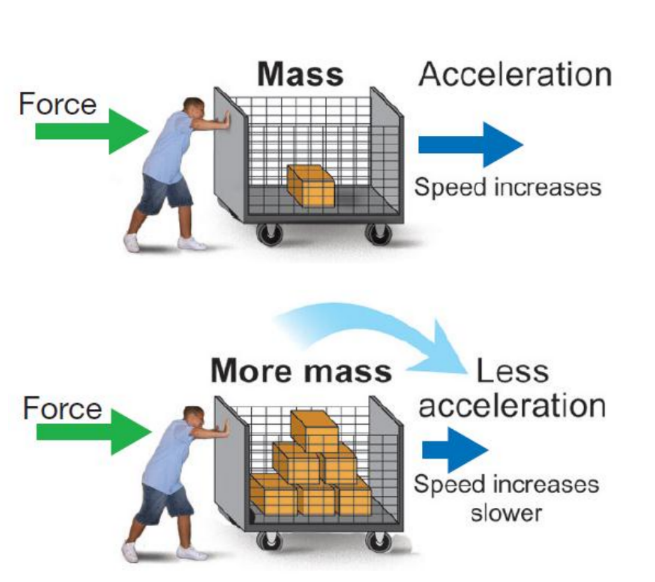
• If the same force is applied to an object with greater mass, the object accelerates at a slower rate because mass adds inertia.
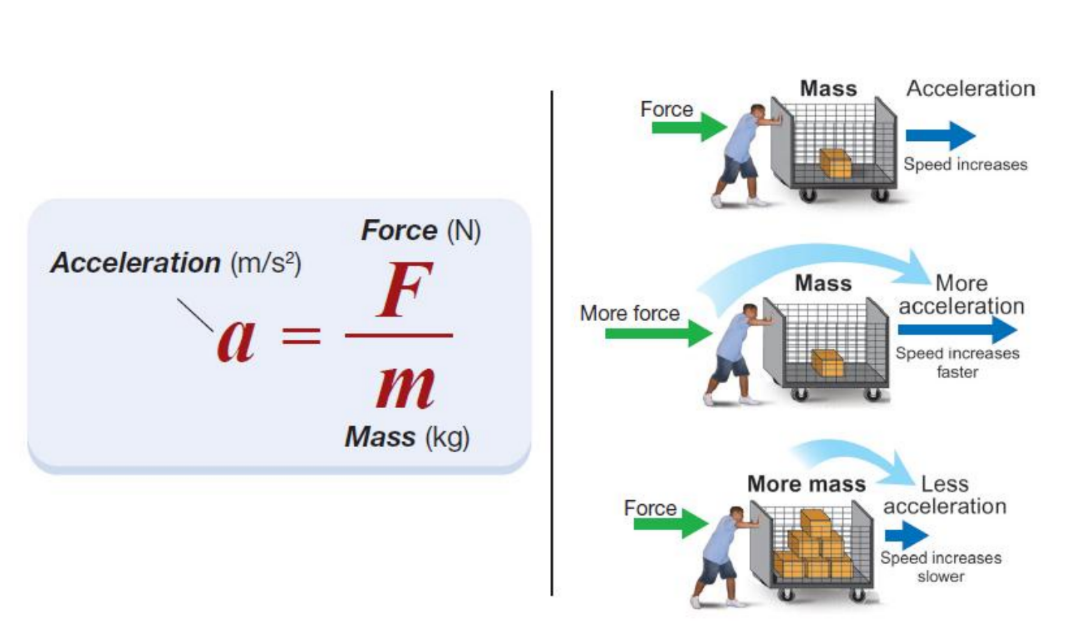
Mass will resist changes in motion
- When you are standing on a bus, and the bus starts very quickly, your body seems to be pushed backward, and if the bus stops suddenly, then your body seems to be pushed forwards. Notice that when the bus turns left, you will seem to be pushed to the right, and when the bus turns right, you will seem to be pushed to the left.
- Also consider a full shopping cart. If you try to push it from a stationary position, it will take some effort to get it moving. The same is true if you try to stop it when it is moving at a high speed, or try to turn it left or right.
Mass will resist changes in motion (continued)
- In both cases, an object with mass is opposing a change in motion. In the first case, it is your body that tries to stay moving as it was before the change. Your body also tries to stay in a straight line when the bus turns, although it appears to be moving to the side.
- What is really happening is that your body is still moving straight and the bus turns in the opposite direction. The shopping cart exhibits the same behavior. When it is stationary, it tries to stay stationary, and when you try to stop it moving, it will try to continue. Your body and the cart both have mass.
Mass will resist changes in motion (continued)
- From this, we can define a property of mass: Mass will resist changes in motion.
- This says that any object with mass will resist any change in motion.
- Objects with greater mass will resist change in motion more than objects with less mass.
- In the SI system, the unit of mass is the kilogram (kg).
Unit of Force
- A force of one Newton is exactly the amount of force needed to cause a mass of one kilogram to accelerate at one $\mathrm{m} / \mathrm{s}^2$.
- We call the unit of force the Newton (N).
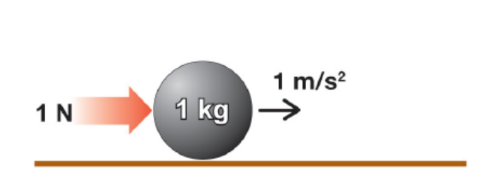
Units
More about F = ma
If you double the mass, you double the force. If you double the acceleration, you double the force.
What if you double the mass and the acceleration?
$
(2 \mathrm{~m})(2 \mathrm{a})=4 \mathrm{~F}
$
Doubling the mass and the acceleration quadruples the force.
What does $\boldsymbol{F}=\operatorname{ma}$ say?
$
F=m a
$
basically means that the force of an object comes from its mass and its acceleration.
Weight as the effect of a gravitational field on a mass
- In everyday usage the term “weight” is commonly used to mean mass, which scientifically is an entirely different concept.
- On the surface of the Earth, the acceleration due to gravity (the “strength of gravity”) is approximately constant; this means that the ratio of the weight force of a motionless object on the surface of the Earth to its mass is almost independent of its location, so that an object’s weight force can stand as a proxy for its mass, and vice versa.
Definition of Weight
- The word weight denotes a quantity of the same nature as a force.
- The weight of a body is the product of its mass and the acceleration due to gravity.
Newton’s Second Law Definitions
Differential Form: $\quad$ Force = change of momentum $\quad \begin{gathered}\text { with change of time }\end{gathered} \frac{d(m v)}{\mathrm{dt}}$
or
Force $=$ change in mass $X$ velocity with time $F=\frac{\left(m_1 V_1-m_0 V_0\right)}{\left(t_1-t_0\right)}$
With mass constant: $\quad$ Force $=$ mass $\mathrm{X}$ acceleration $\quad F=\mathrm{m}$ a
Force, acceleration, momentum and velocity are all vector quantities.
Each has both a magnitude and a direction.
Using the second law of motion
- The force $F$ that appears in the second law is the net force.
- There are often many forces acting on the same object.
- Acceleration results from the combined action of all the forces that act on an object.
- When used this way, the word net means “total.”
- To solve problems with multiple forces, you have to add up all the forces to get a single net force before you can calculate any resulting acceleration.
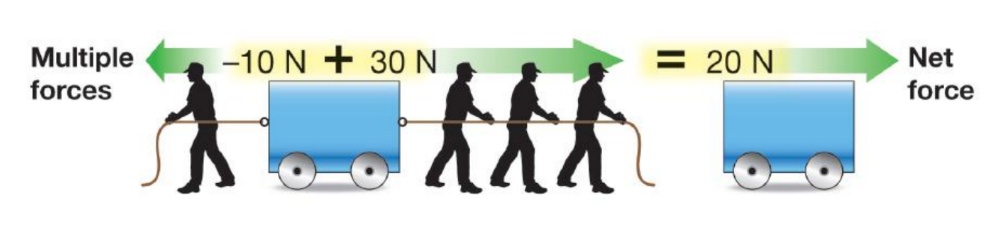
Calculating acceleration
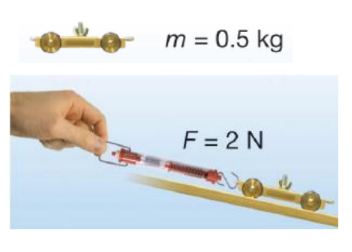
A cart rolls down a ramp. Using a spring scale, you measure a net force of 2 newtons pulling the car down. The cart has a mass of 500 grams $(0.5 \mathrm{~kg})$. Calculate the acceleration of the cart.
1. You are asked for the acceleration $(a)$.
2. You are given mass $(m)$ and force $(F)$.
3. Newton’s second law applies: $a=F \div m$
4. Plug in numbers. (Remember: $1 \mathrm{~N}=1 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^2$ )
Three forms of the second law
Finding the acceleration of moving objects
- The word dynamics refers to problems involving motion.
- In dynamics problems, the second law is often used to calculate the acceleration of an object when you know the force and mass.
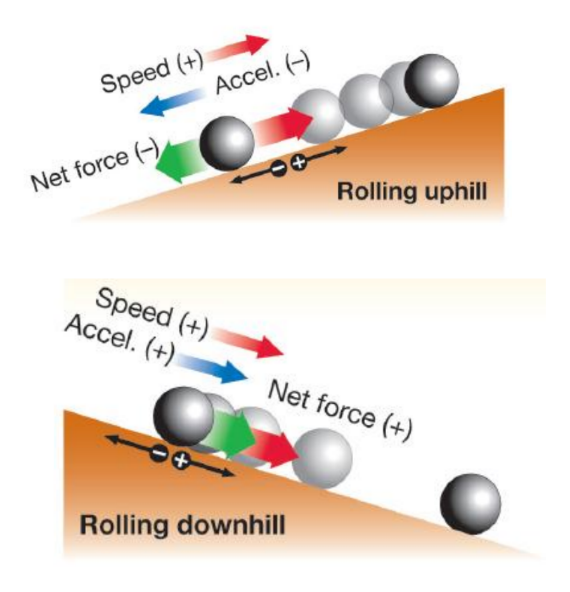
- Speed increases when the net force is in the same direction as the motion.
- Speed decreases when the net force is in the opposite direction as the motion.
Positive and negative acceleration
• We often use positive and negative numbers to show the direction of force and acceleration.
• A common choice is to make velocity, force, and acceleration positive when they point to the right.
Acceleration from multiple forces
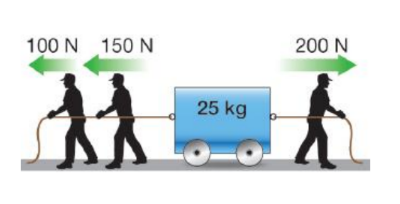
Three people are pulling on a wagon applying forces of 100 N, 150 N, and 200 N. Determine the acceleration and the direction the wagon moves. The wagon has a mass of 25 kilograms.
1. You are asked for the acceleration (a) and direction
2. You are given the forces $(F)$ and mass $(m)$.
3. The second law relates acceleration to force and mass: $a=F \div m$
4. Assign positive and negative directions. Calculate the net force then use the second law to determine the acceleration from the net force and the mass.
Finding force from acceleration
- Wherever there is acceleration there must also be force.
- Any change in the motion of an object results from acceleration.
- Therefore, any change in motion must be caused by force.
Coming back to…Free Fall Motion
- As learned in an earlier chapter, free fall is a special type of motion in which the only force acting upon an object is gravity. Objects that are said to be undergoing free fall, are not encountering a significant force of air resistance; they are falling under the sole influence of gravity.
- Under such conditions, all objects will fall with the same rate of acceleration, regardless of their mass. But why?
- Consider the free-falling motion of a 1000-kg baby elephant and a 1-kg overgrown mouse.
$\mathrm{m}=1001 \mathrm{~kg}$ $\mathrm{m}=1 \mathrm{~kg}$
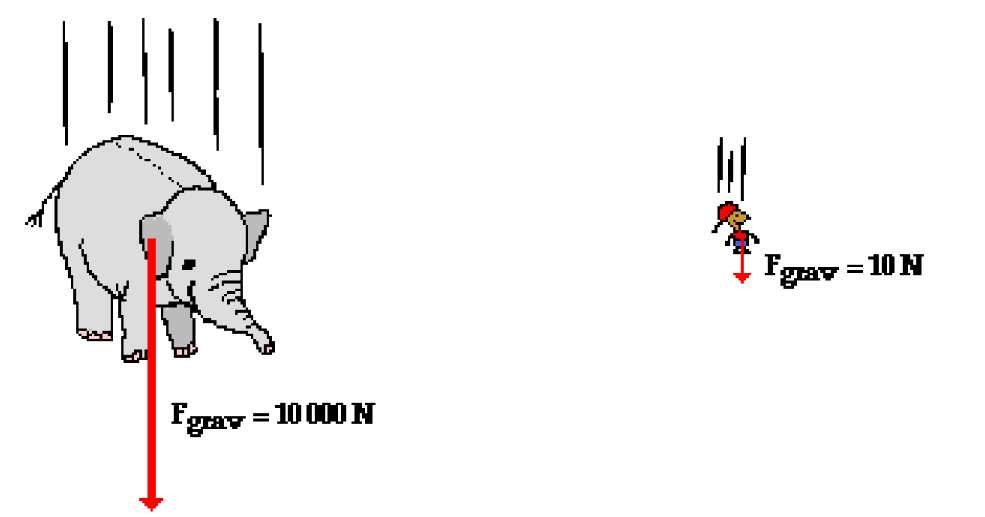
$\begin{gathered}a=\frac{F_{\text {mat }}}{\mathrm{m}}=\frac{10000 \mathrm{H}}{10001 \mathrm{gg}} \\ \mathrm{a}=10 \mathrm{~m} / \mathrm{s} / \mathrm{s}\end{gathered}$ $\begin{gathered}a=\frac{F_{\text {met }}}{m}=\frac{10 h}{11 \mathrm{hg}} \\ \mathrm{A}=10 \mathrm{~m} / \mathrm{s}\end{gathered}$
Explanation on free fall….based on previous diagram
- If Newton’s second law were applied to their falling motion, and if a free-body diagram were constructed, then it would be seen that the 1000-kg baby elephant would experiences a greater force of gravity. This greater force of gravity would have a direct affect upon the elephant’s acceleration; thus, based on force alone, it might be thought that the 1000-kg baby elephant would accelerate faster. But acceleration depends upon two factors: force and mass. The 1000-kg baby elephant obviously has more mass (or inertia). This increased mass has an inverse affect upon the elephant’s acceleration. And thus, the direct affect of greater force on the 1000-kg elephant is offset by the inverse affect of the greater mass of the $1000-\mathrm{kg}$ elephant; and so each object accelerates at the same rate – approximately $10 \mathrm{~m} / \mathrm{s} / \mathrm{s}$. The ratio of force to mass $\left(F_{n e t} / \mathrm{m}\right)$ is the same for the elephant and the mouse under situations involving free fall.
- This ratio $\left(\mathrm{F}_{\text {net }} / \mathrm{m}\right)$ is sometimes called the gravitational field strength and is expressed as $9.8 \mathrm{~N} / \mathrm{kg}$ (for a location upon Earth’s surface). The gravitational field strength is a property of the location within Earth’s gravitational field and not a property of the baby elephant nor the mouse. All objects placed upon Earth’s surface will experience this amount of force $(9.8 \mathrm{~N})$ upon every 1 kilogram of mass within the object. Being a property of the location within Earth’s gravitational field and not a property of the free falling object itself, all objects on Earth’s surface will experience this amount of force per mass. As such, all objects free fall at the same rate regardless of their mass. Because the $9.8 \mathrm{~N} / \mathrm{kg}$ gravitational field at Earth’s surface causes a $9.8 \mathrm{~m} / \mathrm{s}^2$ acceleration of any object placed there, we often call this ratio the acceleration of gravity
Question 1
- Determine the accelerations that result when a $12-\mathrm{N}$ net force is applied to a 3-kg object and then to a 6-kg object.
Answer/Explanation
Answer
- Determine the accelerations that result when a $12-\mathrm{N}$ net force is applied to a $3-\mathrm{kg}$ object and then to a 6-kg object.
- Answer : A 3-kg object experiences an acceleration of $4 \mathrm{~m} / \mathrm{s}^2$. A 6-kg object experiences an acceleration of $2 \mathrm{~m} / \mathrm{s}^2$
Question 2
- Suppose that a sled is accelerating at a rate of $2 \mathrm{~m} / \mathrm{s}^2$. If the net force is tripled and the mass is doubled, then what is the new acceleration of the sled?
Answer/Explanation
Answer
- Suppose that a sled is accelerating at a rate of $2 \mathrm{~m} / \mathrm{s}^2$. If the net force is tripled and the mass is doubled, then what is the new acceleration of the sled?
- Answer: $3 \mathrm{~m} / \mathrm{s}^2$
- The original value of $2 \mathrm{~m} / \mathrm{s}^2$ must be multiplied by 3 (since a and $F$ are directly proportional) and divided by 2 (since $a$ and $m$ are inversely proportional)
Question 3
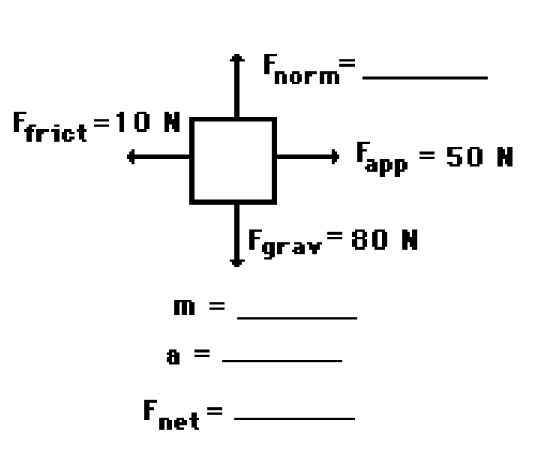
- An applied force of $50 \mathrm{~N}$ is used to accelerate an object to the right across a frictional surface. The object encounters $10 \mathrm{~N}$ of friction. Use the diagram to determine the normal force, the net force, the mass, and the acceleration of the object. (Neglect air resistance.)
Answer/Explanation
Answer
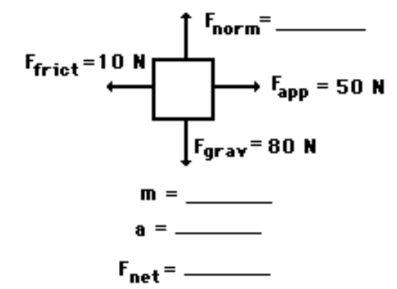
- Note: To simplify calculations, an approximated value of $g$ is often used as $10 \mathrm{~m} / \mathrm{s}^2$
- $F_{n o r m}=80 \mathrm{~N} ; \mathrm{m}=8.16 \mathrm{~kg} ; F_{n e t}=40 \mathrm{~N}$, right; $a=4.9 \mathrm{~m} / \mathrm{s}^2$, right
- (If you are using $g=10, F_{\text {norm }}=80 \mathrm{~N} ; \mathrm{m}=8 \mathrm{~kg} ; F_{n e t}=40 \mathrm{~N}$, right; $a=5$ $\mathrm{m} / \mathrm{s}^2$, right )
- Since there is no vertical acceleration, normal force = gravity force. The mass can be found using the equation $\mathrm{F}_{\text {grav }}=\mathrm{mg}$
- The $F_{\text {net }}$ is the vector sum of all the forces: $80 \mathrm{~N}$, up plus $80 \mathrm{~N}$, down equals $0 \mathrm{~N}$. And $50 \mathrm{~N}$, right plus $10 \mathrm{~N}$, left $=40 \mathrm{~N}$, right.
- Finally, $a=F_{n e t} / \mathrm{m}=(40 \mathrm{~N}) /(8.16 \mathrm{~kg})=4.9 \mathrm{~m} / \mathrm{s}^2$.
Question 4
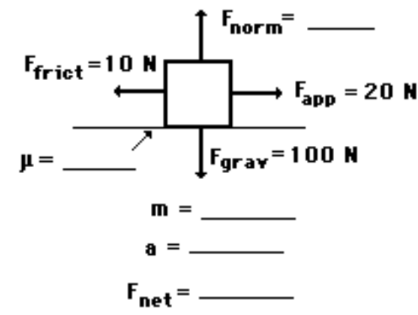
- An applied force of $20 \mathrm{~N}$ is used to accelerate an object to the right across a frictional surface. The object encounters $10 \mathrm{~N}$ of friction. Use the diagram to determine the normal force, the net force, the coefficient of friction $(\mu)$ between the object and the surface, the mass, and the acceleration of the object. (Neglect air resistance.)
- The coefficient of friction (COF), often symbolized by the Greek letter $\mu$, is a dimensionless scalar value which describes the ratio of the force of friction between two bodies and the force pressing them together. The coefficient of friction depends on the materials used; for example, ice on steel has a low coefficient of friction, while rubber on pavement has a high coefficient of friction.
Answer/Explanation
Answer 4
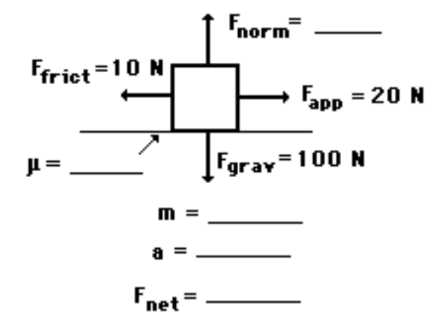
- $F_{\text {norm }}=100 \mathrm{~N} ; m=10.2 \mathrm{~kg} ; F_{\text {net }}=10 \mathrm{~N}$, right; “mu” $=0.1 ; a=0.980$ $\mathrm{m} / \mathrm{s}^2$, right
- (If you are using $g=10, F_{\text {norm }}=100 \mathrm{~N} ; \mathrm{m}=10 \mathrm{~kg} ; \mathrm{F}_{\text {net }}=10 \mathrm{~N}$, right; “mu” $=0.1 ; a=1 \mathrm{~m} / \mathrm{s}^2$, right )
- Since there is no vertical acceleration, the normal force is equal to the gravity force. The mass can be found using the equation $\mathrm{F}_{\text {grav }}=$ $\mathrm{m}$ g.
- Using “mu” $=F_{\text {frict }} / F_{\text {norm }}$ ” $m$ mul $^{-}=(10 \mathrm{~N}) /(100 \mathrm{~N})=0.1$.
- The $F_{\text {net }}$ is the vector sum of all the forces: $100 \mathrm{~N}$, up plus $100 \mathrm{~N}$, down equals $0 \mathrm{~N}$. And $20 \mathrm{~N}$, right plus $10 \mathrm{~N}$, left = $10 \mathrm{~N}$, right.
- Finally, $a=F_{n e t} / \mathrm{m}=(10 \mathrm{~N}) /(10.2 \mathrm{~kg})=0.980 \mathrm{~m} / \mathrm{s}^2$.
Equilibrium
- The condition of zero acceleration is called equilibrium.
- In equilibrium, all forces cancel out leaving zero net force.
- Objects that are standing still are in equilibrium because their acceleration is zero.
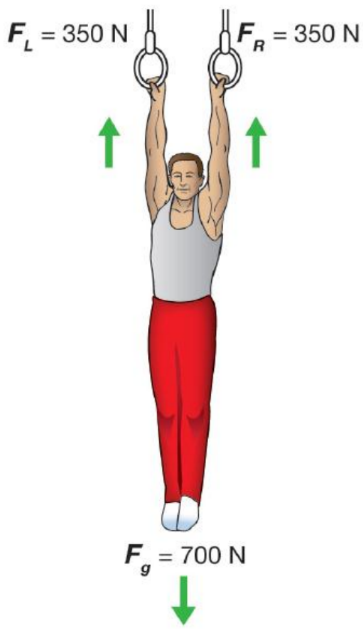
- Objects that are moving at constant speed and direction are also in equilibrium.
- A static problem usually means there is no motion.
Calculating force
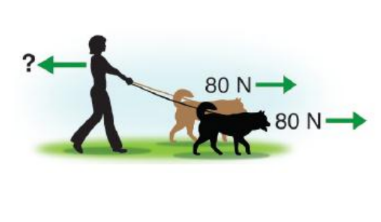
A woman is holding two dogs on a leash. If each dog pulls with a force of 80 Newtons, how much force does the woman have to exert to keep the dogs from moving?
1. You are asked for force $(F)$.
2. You are given two $80 \mathrm{~N}$ forces and the fact that the dogs are not moving $(a=0)$.
3. Newton’s second law says the net force must be zero if the acceleration is zero.
4. The woman must exert a force equal and opposite to the sum of the forces from the two dogs.
Who is wrong here? Anna or Noah?
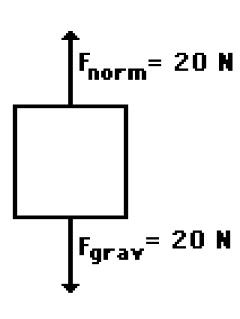
- Two students are discussing on an object that is being acted upon by two individual forces (both in a vertical direction). During the discussion, Anna suggests to Noah that the object under discussion could be moving. In fact, Anna suggests that if friction and air resistance could be ignored (because of their negligible size), the object could be moving in a horizontal direction. According to Anna, an object experiencing forces as described at the right could be experiencing a horizontal motion.
- Noah objects, arguing that the object could not have any horizontal motion if there are only vertical forces acting upon it. Noah claims that the object must be at rest, perhaps on a table or floor. After all, says Noah, an object experiencing a balance of forces will be at rest. Who do you agree with?
Answer/Explanation
Answer
• Anna is correct.
• Noah may know the formulas but he does not know (or does not believe) Newton’s laws. If the forces acting on an object are balanced and the object is in motion, then it will continue in motion with the same velocity.
• Remember: forces do not cause motion. Forces cause accelerations.
Newton’s Third Law

Newton’s third law of motion…..
• For every action there is an equal and opposite reaction.
What does this mean?

For every force acting on an object, there is an equal force acting in the opposite direction.
Right now, gravity is pulling you down in your seat, but Newton’s Third Law says your seat is pushing up against you with equal force. This is why you are not moving. There is a balanced force acting on you- gravity pulling down, your seat pushing up.
What happens if….

What happens if you are standing on a skateboard or a slippery floor and push against a wall?
You slide in the opposite direction (away from the wall), because you pushed on the wall but the wall pushed back on you with equal and opposite force.
Newton’s Third Law
Rocket Engine Thrust
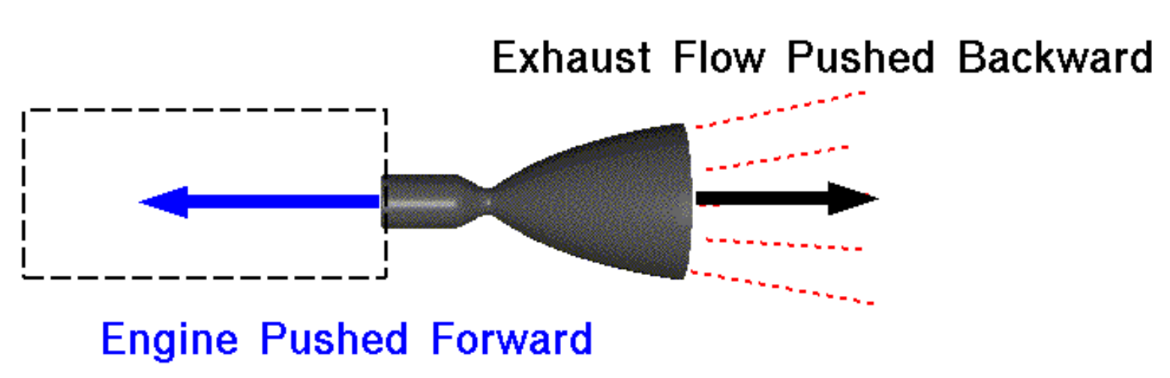
For every action, there is an equal and opposite re-action.
The Third Law: Action and Reaction
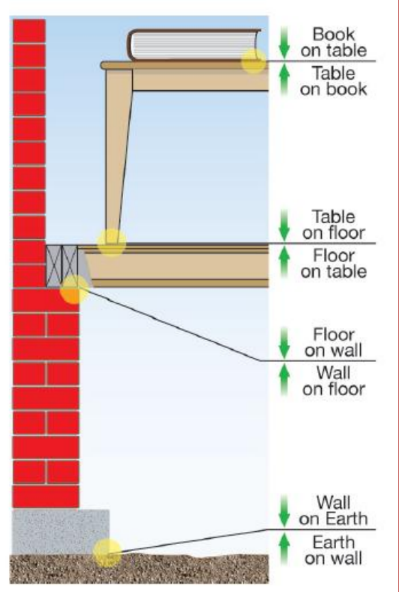
• “For every action there is an equal and opposite reaction.”
• This statement is known as Newton’s third law of motion.
• Newton’s third law discusses pairs of objects and the interactions between them.
Forces occur in pairs
- The astronauts working on the space station have a serious problem when they need to move around in space: There is nothing to push on.
- One solution is to throw something opposite the direction you want to move.
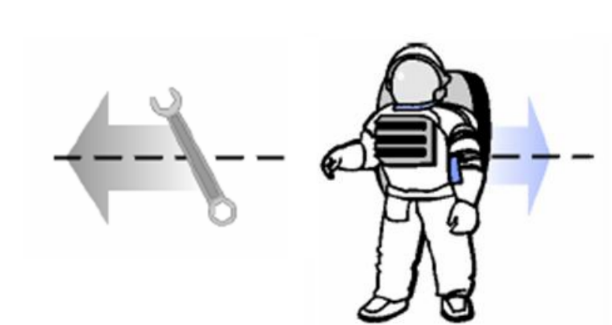
• The two forces in a pair are called action and reaction.
• Anytime you have one, you also have the other.
• If you know the strength of one you also know the strength of the other since both forces are always equal.
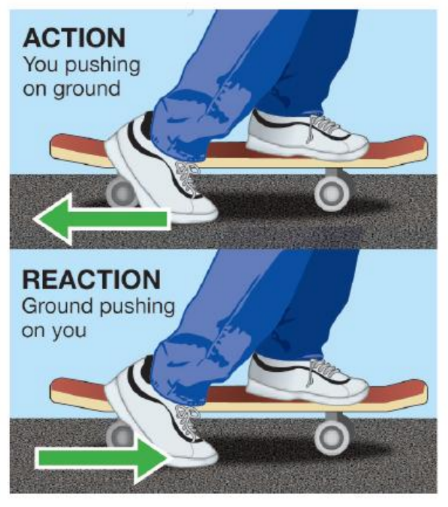
Third Law…
• Action and reaction forces act on different objects, not on the same object.
• The forces cannot cancel because they act on different objects.
Action & Reaction
- The act of moving or the ability to move from one place to another is called locomotion.
- Any animal or machine that moves depends on Newton’s third law to get around.
- When we walk, we push off the ground and move forward because of the ground pushing back on us in the opposite direction.
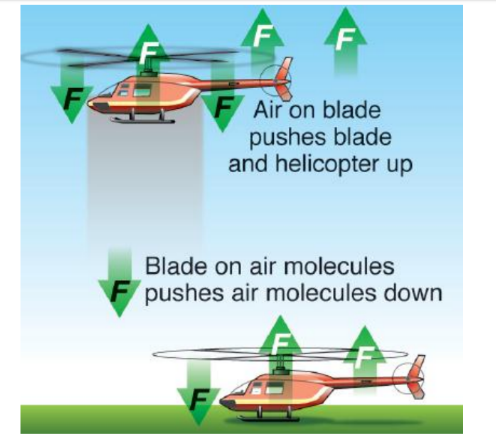
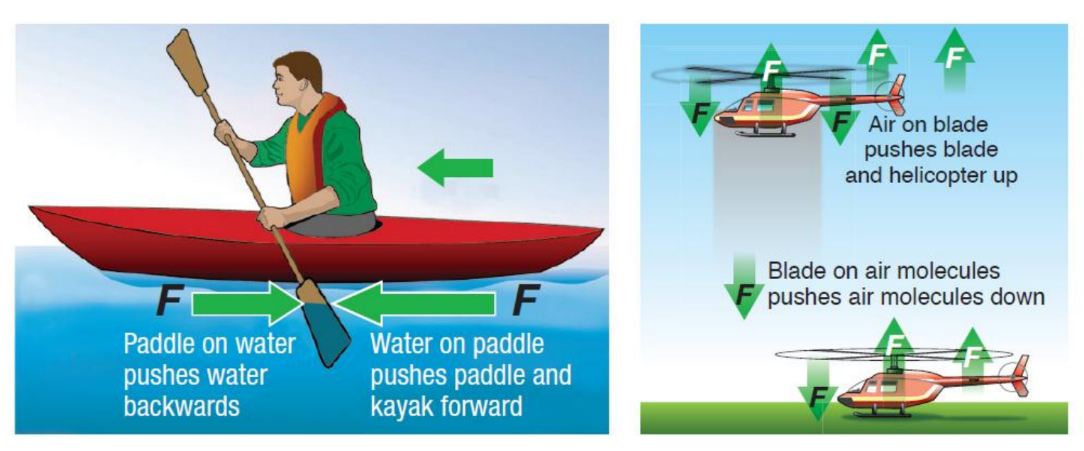
• Jets, planes, and helicopters push air.
• In a helicopter, the blades of the propeller are angled such that when they spin, they push the air molecules down.
The rotor blades of an helicopter are just like the wings of an airplane or a bird. As they move through the air, they pull the air above them downwards. That’s the “action” part of the action-reaction. When the blades push the air downward, the helicopter is lifted. The air has considerable mass and inertia, and resists being pulled down-it tries to push the wings up instead. That’s the “reaction” part, and that’s also aerodynamic lift. The blades pull air downwards, and the reaction to this pushes the helicopter upwards.