[Maximum mark: 18]
Question:
In the following Argand diagram, the points Z1 , O and Z2 are the vertices of triangle Z1OZ2 described anticlockwise.
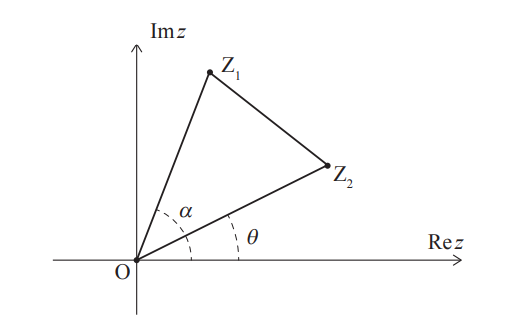
The point Z1 represents the complex number z1 = r1eiα , where r1 > 0. The point Z2 represents the complex number z2 = r2eiθ , where r2 > 0.
Angles α, θ are measured anticlockwise from the positive direction of the real axis such that 0 ≤ α, θ < 2π and 0 < α – θ < π.
(a) Show that z1z2 * = r1r2e i(α – θ) where z2* is the complex conjugate of z2 .
▶️Answer/Explanation
Ans:
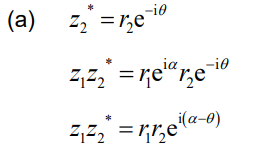
Note: Accept working in modulus-argument form
(b) Given that Re (z1 z2*) = 0, show that Z1OZ2 is a right-angled triangle.
In parts (c), (d) and (e), consider the case where Z1OZ2 is an equilateral triangle.
▶️Answer/Explanation
Ans: 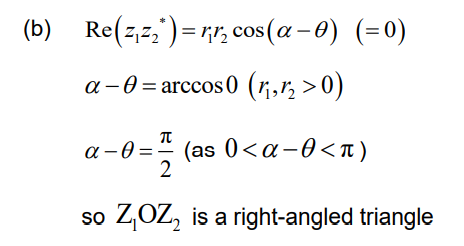
(c) (i) Express z1 in terms of z2 .
(ii) Hence show that z12 + z22 = z1 z2 .
Let z1 and z2 be the distinct roots of the equation z2 + az + b = 0 where z ∈ C and a , b ∈ R.
▶️Answer/Explanation
Ans:
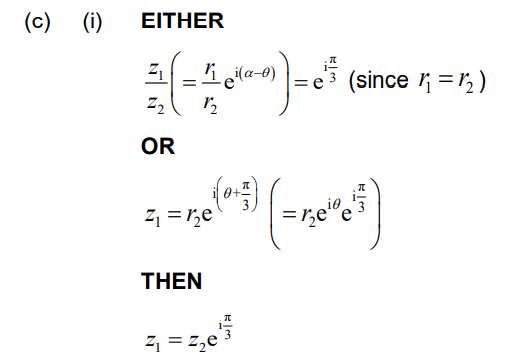
Note: Accept working in either modulus-argument form to obtain \(z_{1} = z_{2}\left ( cos\frac{\pi }{3} + isin\frac{\pi }{3} \right )\) or in Cartesian form to obtain \(z_{1} = z_{2}\left ( \frac{1}{2} + \frac{\sqrt{3}}{2} \right )i\)


(d) Use the result from part (c)(ii) to show that a2 – 3b = 0.
Consider the equation z2 + az + 12 = 0, where z ∈ C and a ∈ R.
▶️Answer/Explanation
Ans: 

(e) Given that 0 < α – θ < π, deduce that only one equilateral triangle Z1OZ2 can be formed from the point O and the roots of this equation.
▶️Answer/Explanation
Ans:
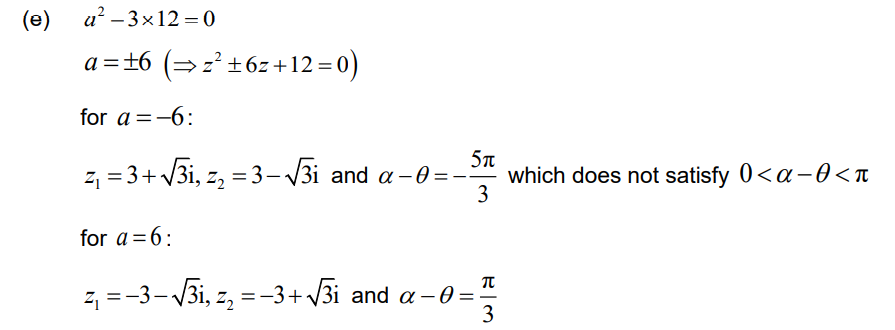
so (for 0 < α – θ < π), only one equilateral triangle can be formed from point O and the two roots of this equation
Question
Consider the equation \(\frac{2z}{3-z}\) = i where z = x + i y and x , y ∈ R.
Find the value of x and the value of y . [Maximum mark: 5]
▶️Answer/Explanation
Ans:
substituting z = x + iy and *z = x – iy
\(\frac{2(x+iy)}{3-(x-iy)}\)=i
2x+2iy = -y + i (3-x)
equate real and imaginary:
y= -2x AND 2y= 3-x
solving simultaneously: x= -1, y=2 (z=-1+2i)
Question
Given that \({z_1} = 2\) and \({z_2} = 1 + \sqrt 3 {\text{i}}\) are roots of the cubic equation \({z^3} + b{z^2} + cz + d = 0\) where b, c, \(d \in \mathbb{R}\),
(a) write down the third root, \({z_3}\), of the equation;
▶️Answer/Explanation
Ans: \(1 – \sqrt 3 {\text{i}}\) A1
▶️Answer/Explanation
Ans:
EITHER
\(\left( {z – (1 + \sqrt 3 {\text{i)}}} \right)\left( {z – (1 – \sqrt 3 {\text{i)}}} \right) = {z^2} – 2z + 4\) (M1)A1
\(p(z) = (z – 2)({z^2} – 2z + 4)\) (M1)
\( = {z^3} – 4{z^2} + 8z – 8\) A1
therefore \(b = – 4,{\text{ }}c = 8,{\text{ }}d = – 8\)
OR
relating coefficients of cubic equations to roots
\( – b = 2 + 1 + \sqrt 3 {\text{i}} + 1 – \sqrt 3 {\text{i}} = 4\) M1
\(c = 2(1 + \sqrt 3 {\text{i}}) + 2(1 – \sqrt 3 {\text{i}}) + (1 + \sqrt 3 {\text{i}})(1 – \sqrt 3 {\text{i}}) = 8\)
\( – d = 2(1 + \sqrt 3 {\text{i}})(1 – \sqrt 3 {\text{i}}) = 8\)
\(b = – 4,{\text{ }}c = 8,{\text{ }}d = – 8\) A1A1A1
▶️Answer/Explanation
Ans: \({z_2} = 2{{\text{e}}^{\frac{{{\text{i}}\pi }}{3}}},{\text{ }}{z_3} = 2{{\text{e}}^{ – \frac{{{\text{i}}\pi }}{3}}}\) A1A1A1
Note: Award A1 for modulus,
A1 for each argument.
[8 marks]
Question
Let \(z = \cos \theta + i\sin \theta \).
a. Use de Moivre’s theorem to find the value of \({\left( {\cos \left( {\frac{\pi }{3}} \right) + {\text{i}}\sin \left( {\frac{\pi }{3}} \right)} \right)^3}\).[2]
▶️Answer/Explanation
Ans:
\({\left( {\cos \left( {\frac{\pi }{3}} \right) + {\text{i}}\sin \left( {\frac{\pi }{3}} \right)} \right)^3} = \cos \pi + {\text{i}}\sin \pi \) M1
\( = – 1\) A1
[2 marks]
\[{(\cos \theta – {\text{i}}\sin \theta )^n} = \cos n\theta – {\text{i}}\sin n\theta {\text{ for }}n \in {\mathbb{Z}^ + }.\][6]
▶️Answer/Explanation
Ans:
show the expression is true for \(n = 1\) R1
assume true for \(n = k,{\text{ }}{(\cos \theta – {\text{i}}\sin \theta )^k} = \cos k\theta – {\text{i}}\sin k\theta \) M1
Note: Do not accept “let \(n = k\)” or “assume \(n = k\)”, assumption of truth must be present.
\({(\cos \theta – {\text{i}}\sin \theta )^{k + 1}} = {(\cos \theta – {\text{i}}\sin \theta )^k}(\cos \theta – {\text{i}}\sin \theta )\)
\( = (\cos k\theta – {\text{i}}\sin k\theta )(\cos \theta – {\text{i}}\sin \theta )\) M1
\( = \cos k\theta \cos \theta – \sin k\theta \sin \theta – {\text{i}}(\cos k\theta \sin \theta + \sin k\theta \cos \theta )\) A1
Note: Award A1 for any correct expansion.
\( = \cos \left( {(k + 1)\theta } \right) – {\text{i}}\sin \left( {(k + 1)\theta } \right)\) A1
therefore if true for \(n = k\) true for \(n = k + 1\), true for \(n = 1\), so true for all \(n( \in {\mathbb{Z}^ + })\) R1
Note: To award the final R mark the first 4 marks must be awarded.
[6 marks]
c. Find an expression in terms of \(\theta \) for \({(z)^n} + {(z{\text{*}})^n},{\text{ }}n \in {\mathbb{Z}^ + }\) where \(z{\text{*}}\) is the complex conjugate of \(z\).[2]
▶️Answer/Explanation
Ans:
\({(z)^n} + {(z{\text{*}})^n} = {(\cos \theta + {\text{i}}\sin \theta )^n} + {(\cos \theta – {\text{i}}\sin \theta )^n}\)
\( = \cos n\theta + {\text{i}}\sin n\theta + \cos n\theta – {\text{i}}\sin n\theta = 2\cos (n\theta )\) (M1)A1
[2 marks]
▶️Answer/Explanation
Ans:
\(zz* = (\cos \theta + {\text{i}}\sin \theta )(\cos \theta – {\text{i}}\sin \theta )\)
\( = {\cos ^2}\theta + {\sin ^2}\theta \) A1
\( = 1\) AG
Note: Allow justification starting with \(|z| = 1\).
(ii) Write down the binomial expansion of \({(z + z{\text{*}})^3}\) in terms of \(z\) and \(z{\text{*}}\).
▶️Answer/Explanation
Ans: \({(z + z{\text{*}})^3} = {z^3} + 3{z^2}z{\text{*}} + 3z{({z^*})^2} + (z{\text{*}})3\left( { = {z^3} + 3z + 3z{\text{*}} + {{(z{\text{*}})}^3}} \right)\) A1
▶️Answer/Explanation
Ans:
\({(z + z{\text{*}})^3} = {(2\cos \theta )^3}\) A1
\({z^3} + 3z + 3z{\text{*}} + {(z{\text{*}})^3} = 2\cos 3\theta + 6\cos \theta \) M1A1
\(\cos 3\theta = 4{\cos ^3}\theta – 3\cos \theta \) AG
Note: M1 is for using \(zz{\text{*}} = 1\), this might be seen in d(ii).
[5 marks]
e. Hence solve \(4{\cos ^3}\theta – 2{\cos ^2}\theta – 3\cos \theta + 1 = 0\) for \(0 \leqslant \theta < \pi \).[6]
▶️Answer/Explanation
Ans:
\(4{\cos ^3}\theta – 2{\cos ^2}\theta – 3\cos \theta + 1 = 0\)
\(4{\cos ^3}\theta – 3\cos \theta = 2{\cos ^2}\theta – 1\)
\(\cos (3\theta ) = \cos (2\theta )\) A1A1
Note: A1 for \(\cos (3\theta )\) and A1 for \(\cos (2\theta )\).
\(\theta = 0\) A1
or \(3\theta = 2\pi – 2\theta {\text{ }}({\text{or }}3\theta = 4\pi – 2\theta )\) M1
\(\theta = \frac{{2\pi }}{5},{\text{ }}\frac{{4\pi }}{5}\) A1A1
Note: Do not accept solutions via factor theorem or other methods that do not follow “hence”.
[6 marks]