[Maximum mark: 6]
Question:
Consider any three consecutive integers, n – 1, n and n + 1.
(a) Prove that the sum of these three integers is always divisible by 3.
▶️Answer/Explanation
Ans: (n – 1) + n + (n + 1)
= 3n
which is always divisible by 3
(b) Prove that the sum of the squares of these three integers is never divisible by 3.
▶️Answer/Explanation
Ans: (n -1)2 +n2 + (n+1)2 (=n2 – 2n + 1 + n2 + n2 + 2n + 1)
attempts to expand either (n -1)2 or (n+1)2 ( do not accept n2 – 1 or n2 + 1)
= 3n2 + 2
demonstrating recognition that 2 is not divisible by 3 or \(\frac{2}{3}\) seen after correct
expression divided by 3
3n2 is divisible by 3 and so 3n2 + 2 is never divisible by 3
OR the first term is divisible by 3, the second is not
OR \(3\left ( n^{2}+\frac{2}{3} \right ) OR \frac{3n^{2} + 2}{3} = n^{2} + \frac{2}{3}\)
hence the sum of the squares is never divisible by 3
Question
Consider the following equations, where a , \(b \in \mathbb{R}:\)
\(x + 3y + (a – 1)z = 1\)
\(2x + 2y + (a – 2)z = 1\)
\(3x + y + (a – 3)z = b.\)
a. If each of these equations defines a plane, show that, for any value of a , the planes do not intersect at a unique point.[3]
▶️Answer/Explanation
Ans:
METHOD 1
\(\det \left( {\begin{array}{*{20}{c}}
1&3&{a – 1} \\
2&2&{a – 2} \\
3&1&{a – 3}
\end{array}} \right)\) M1
\( = 1\left( {2(a – 3) – (a – 2)} \right) – 3\left( {2(a – 3) – 3(a – 2)} \right) + (a – 1)(2 – 6)\)
(or equivalent) A1
= 0 (therefore there is no unique solution) A1
[3 marks]
METHOD 2
\(\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
2&2&{a – 2}\\
3&1&{a – 3}
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
1\\
▶️Answer/Explanatio
Ans:
\end{array}} \right):\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
0&{ – 4}&{ – a}\\
0&{ – 8}&{ – 2a}
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
{b – 3}
\end{array}} \right)\) M1A1
\(:\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
0&{ – 4}&{ – a}\\
0&0&0
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
{b – 1}
\end{array}} \right)\) (and 3 zeros imply no unique solution) A1
[3 marks]
METHOD 1
\(\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
2&2&{a – 2}\\
3&1&{a – 3}
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
1\\
b
\end{array}} \right):\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
0&{ – 4}&{ – a}\\
0&{ – 8}&{ – 2a}
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
{b – 3}
\end{array}} \right)\) M1A1
\(:\left( {\begin{array}{*{20}{c}}
1&3&{a – 1}\\
0&{ – 4}&{ – a}\\
0&0&0
\end{array}} \right|\left. {\begin{array}{*{20}{c}}
1\\
{ – 1}\\
{b – 1}
\end{array}} \right)\) A1
b = 1 A1 N2
Note: Award M1 for an attempt to use row operations.
[4 marks]
METHOD 2
b = 1 A4
Note: Award A4 only if “ b −1 ” seen in (a).
[4 marks]
Question
(a) Show that the following system of equations has an infinite number of solutions.
\(x + y + 2z = – 2\)
\(3x – y + 14z = 6\)
\(x + 2y = – 5\)
The system of equations represents three planes in space.
▶️Answer/Explanation
Ans:
EITHER
\(\left( {\begin{array}{*{20}{c}}1&1&2\\3&{ – 1}&{14}\\1&2&0\end{array}\left| \begin{array}{c} – 2\\6\\ – 5\end{array} \right.} \right) \to \left( {\begin{array}{*{20}{c}}1&1&2\\0&1&{ – 2}\\0&0&0\end{array}\left| \begin{array}{c} – 2\\ – 3\\0\end{array} \right.} \right)\) M1
row of zeroes implies infinite solutions, (or equivalent). R1
Note: Award M1 for any attempt at row reduction.
OR
\(\left| {\begin{array}{*{20}{c}}1&1&2\\3&{ – 1}&{14}\\1&2&0\end{array}} \right| = 0\) M1
\(\left| {\begin{array}{*{20}{c}}1&1&2\\3&{ – 1}&{14}\\1&2&0\end{array}} \right| = 0\) with one valid point R1
OR
\(x + y + 2z = – 2\)
\(3x – y + 14z = 6\)
\(x + 2y = – 5\) \( \Rightarrow x = – 5 – 2y\)
substitute \(x = – 5 – 2y\) into the first two equations:
\( – 5 – 2y + y + 2z = – 2\)
\(3( – 5 – 2y) – y + 14z = 6\) M1
\( – y + 2z = 3\)
\( – 7y + 14z = 21\)
the latter two equations are equivalent (by multiplying by 7) therefore an infinite number of solutions. R1
OR
for example, \(7 \times {{\text{R}}_1} – {{\text{R}}_2}\) gives \(4x + 8y = – 20\) M1
this equation is a multiple of the third equation, therefore an infinite
number of solutions. R1
[2 marks]
(b) Find the parametric equations of the line of intersection of the three planes.
▶️Answer/Explanation
Ans:
let \(y = t\) M1
then \(x = – 5 – 2t\) A1
\(z = \frac{{t + 3}}{2}\) A1
OR
let \(x = t\) M1
then \(y = \frac{{ – 5 – t}}{2}\) A1
\(z = \frac{{1 – t}}{4}\) A1
OR
let \(z = t\) M1
then \(x = 1 – 4t\) A1
\(y = – 3 + 2t\) A1
OR
attempt to find cross product of two normal vectors:
eg: \(\left| {\begin{array}{*{20}{c}}i&j&k\\1&1&2\\1&2&0\end{array}} \right| = – 4i + 2j + k\) M1A1
\(x = 1 – 4t\)
\(y = – 3 + 2t\)
\(z = t\) A1
(or equivalent)
[3 marks]
Total [5 marks]
Question
The following system of equations represents three planes in space.
\[x + 3y + z = – 1\]
\[x + 2y – 2z = 15\]
\[2x + y – z = 6\]
Find the coordinates of the point of intersection of the three planes.
▶️Answer/Explanation
Markscheme
EITHER
eliminating a variable, \(x\), for example to obtain \(y + 3z = – 16\) and \( – 5y – 3z = 8\) M1A1
attempting to find the value of one variable M1
point of intersection is \(( – 1,{\text{ }}2,{\text{ }} – 6)\) A1A1A1
OR
attempting row reduction of relevant matrix, eg. 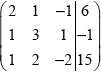 M1
M1
correct matrix with two zeroes in a column, eg. 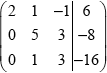 A1
A1
further attempt at reduction M1
point of intersection is \(( – 1,{\text{ }}2,{\text{ }} – 6)\) A1A1A1
Note: Allow solution expressed as \(x = – 1,{\text{ }}y = 2,{\text{ }}z = – 6\) for final A marks.
[6 marks]
Question
a. Consider the following system of equations:
\[x + y + z = 1\]
\[2x + 3y + z = 3\]
\[x + 3y – z = \lambda \]
where \(\lambda \in \mathbb{R}\) .
▶️Answer/Explanation
Ans:
using row operations, M1
to obtain 2 equations in the same 2 variables A1A1
for example \(y – z = 1\)
\(2y – 2z = \lambda – 1\)
the fact that one of the left hand sides is a multiple of the other left hand side indicates that the equations do not have a unique solution, or equivalent R1AG
[4 marks]
(i) Determine the value of \(\lambda \) for which the system is consistent.
▶️Answer/Explanation
Ans: \(\lambda = 3\) A1
▶️Answer/Explanation
Ans:
put \(z = \mu \) M1
then \(y = 1 + \mu \) A1
and \(x = – 2\mu \) or equivalent A1
[4 marks]
Question
Solve the following system of equations:
3x – 2y + z = -4
x + y – z = -2
2x + 3y = 4
▶️Answer/Explanation
Ans
sing an elimination method,
3x – 2y +z = -4
x – y – z = -2
4x – y = -6
4x + 6y = 8
7y = 14
Therefore x = -1, y = 2, z = 3