Question
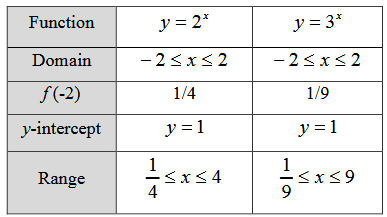
On the same set of axes, sketch the graphs of the following two functions f(x) = ax, -2≤ x ≤ 2 or 2=aand 3. Then complete the table beside. 
▶️Answer/Explanation
Ans
Question
The function f is given by f (x) = 2 – x2 – ex. [Sketch the graph of the function first] Write down (a) the maximum value of f(x). …………………………………….. (b) the two roots of the equation f(x) = 0 ……………………………………..
▶️Answer/Explanation
Ans
(a) \(f_{max}=1.17\) (b) Roots are -1.32, 0.537
Question
Let \(f(x)=\sqrt{x+1}+1\) and g(x) = x2. (a) Solve the equation (g0f)(x)=1 (b) Find the function h(x) given that h0f = g (c) Find the function k(x) given that fok = g
▶️Answer/Explanation
Ans
Let \(f(x)=\sqrt {x+1}+1\) and g(x) = x2. (a) x = -1 (b) h(x) = (x2 – 2x)2 (c) k(x) = x4 – 2x2
Question
Solve the exponential equations:
(a) \(4^x – 9.2^x + 8 = 0\) (b) \(3^{2x+2} + 8(3)^{x+1} = 9\)
▶️Answer/Explanation
Ans
(a) x = 0, x = 3 (b) x = -1
Question
Consider the function f(x) = ex-2.
(a) Find f-1
(b) Sketch the graphs of f and f-1 by indicating clearly any intercepts and asymptotes.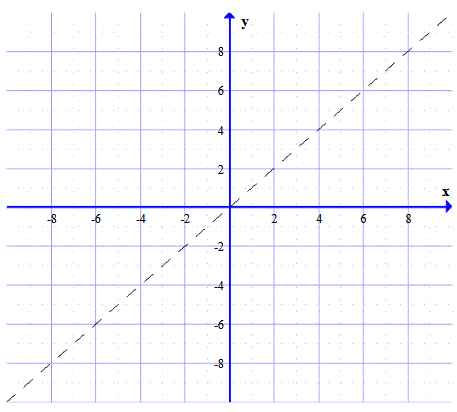
(c) Complete the table
▶️Answer/Explanation
Ans
(a) f-1(x) = In(x +2)
(b) For f, there is no x-intercept, y-intercept: y = e2, Horizontal asymptote: y = 0
For f-1, x-intercept: x = e2, there is no y-intercept, Vertical asymptote: x = 0
(c) For f, Domain: x ∈ R, Range: y>0
For f-1, Domain: x>R, Range: y ∈ R