Question
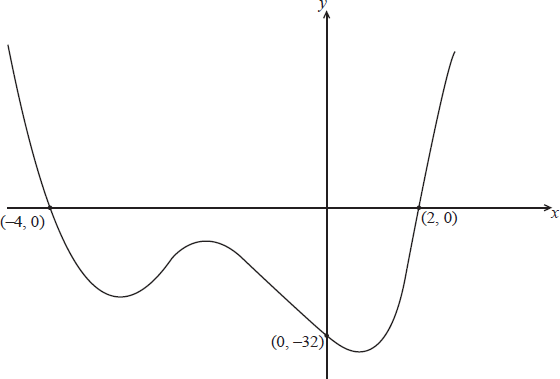
The graph of a polynomial function f of degree 4 is shown below.
Given that \({(x + {\text{i}}y)^2} = – 5 + 12{\text{i}},{\text{ }}x,{\text{ }}y \in \mathbb{R}\) . Show that
(i) \({x^2} – {y^2} = – 5\) ;
(ii) \(xy = 6\) .[2]
Hence find the two square roots of \( – 5 + 12{\text{i}}\) .[5]
For any complex number z , show that \({(z^*)^2} = ({z^2})^*\) .[3]
Hence write down the two square roots of \( – 5 – 12{\text{i}}\) .[2]
Explain why, of the four roots of the equation \(f(x) = 0\) , two are real and two are complex.[2]
The curve passes through the point \(( – 1,\, – 18)\) . Find \(f(x)\) in the form
\(f(x) = (x – a)(x – b)({x^2} + cx + d),{\text{ where }}a,{\text{ }}b,{\text{ }}c,{\text{ }}d \in \mathbb{Z}\) .[5]
Find the two complex roots of the equation \(f(x) = 0\) in Cartesian form.[2]
Draw the four roots on the complex plane (the Argand diagram).[2]
Express each of the four roots of the equation in the form \(r{{\text{e}}^{{\text{i}}\theta }}\) .[6]
▶️Answer/Explanation
Markscheme
(i) \({(x + {\text{i}}y)^2} = – 5 + 12{\text{i}}\)
\({x^2} + 2{\text{i}}xy + {{\text{i}}^2}{y^2} = – 5 + 12{\text{i}}\) A1
(ii) equating real and imaginary parts M1
\({x^2} – {y^2} = – 5\) AG
\(xy = 6\) AG
[2 marks]
substituting M1
EITHER
\({x^2} – \frac{{36}}{{{x^2}}} = – 5\)
\({x^4} + 5{x^2} – 36 = 0\) A1
\({x^2} = 4,\, – 9\) A1
\(x = \pm 2\) and \(y = \pm 3\) (A1)
OR
\(\frac{{36}}{{{y^2}}} – {y^2} = – 5\)
\({y^4} – 5{y^2} – 36 = 0\) A1
\({y^2} = 9,\, – 4\) A1
\({y^2} = \pm 3\) and \(x = \pm 2\) (A1)
Note: Accept solution by inspection if completely correct.
THEN
the square roots are \((2 + 3{\text{i}})\) and \(( – 2 – 3{\text{i}})\) A1
[5 marks]
EITHER
consider \(z = x + {\text{i}}y\)
\(z^* = x – {\text{i}}y\)
\({(z^*)^2} = {x^2} – {y^2} – 2{\text{i}}xy\) A1
\(({z^2}) = {x^2} – {y^2} + 2{\text{i}}xy\) A1
\(({z^2})^* = {x^2} – {y^2} – 2{\text{i}}xy\) A1
\({(z^*)^2} = ({z^2})^*\) AG
OR
\(z^* = r{{\text{e}}^{ – {\text{i}}\theta }}\)
\({(z^*)^2} = {r^2}{{\text{e}}^{ – 2{\text{i}}\theta }}\) A1
\({z^2} = {r^2}{{\text{e}}^{2{\text{i}}\theta }}\) A1
\(({z^2})^* = {r^2}{{\text{e}}^{ – 2{\text{i}}\theta }}\) A1
\({(z^*)^2} = ({z^2})^*\) AG
[3 marks]
\((2 – 3{\text{i}})\) and \(( – 2 + 3{\text{i}})\) A1A1
[2 marks]
the graph crosses the x-axis twice, indicating two real roots R1
since the quartic equation has four roots and only two are real, the other two roots must be complex R1
[2 marks]
\(f(x) = (x + 4)(x – 2)({x^2} + cx + d)\) A1A1
\(f(0) = – 32 \Rightarrow d = 4\) A1
Since the curve passes through \(( – 1,\, – 18)\),
\( – 18 = 3 \times ( – 3)(5 – c)\) M1
\(c = 3\) A1
Hence \(f(x) = (x + 4)(x – 2)({x^2} + 3x + 4)\)
[5 marks]
\(x = \frac{{ – 3 \pm \sqrt {9 – 16} }}{2}\) (M1)
\( \Rightarrow x = – \frac{3}{2} \pm {\text{i}}\frac{{\sqrt 7 }}{2}\) A1
[2 marks]
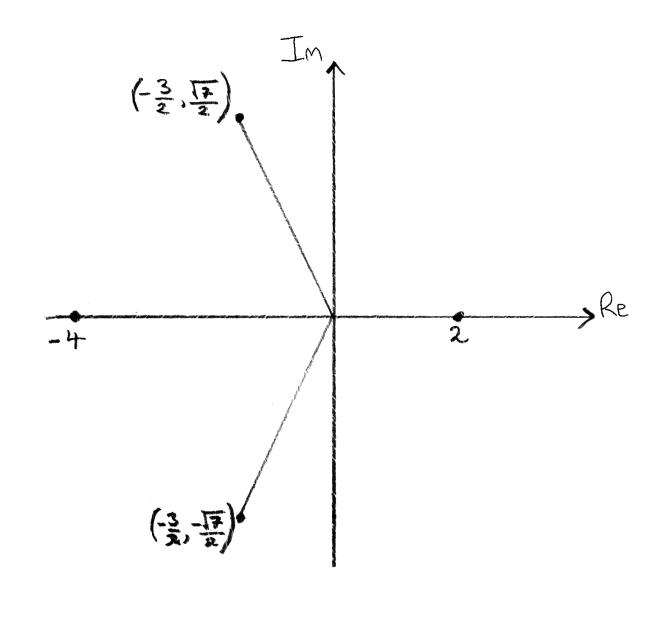 A1A1
A1A1
Note: Accept points or vectors on complex plane.
Award A1 for two real roots and A1 for two complex roots.
[2 marks]
real roots are \(4{{\text{e}}^{{\text{i}}\pi }}\) and \(2{{\text{e}}^{{\text{i}}0}}\) A1A1
considering \( – \frac{3}{2} \pm {\text{i}}\frac{{\sqrt 7 }}{2}\)
\(r = \sqrt {\frac{9}{4} + \frac{7}{4}} = 2\) A1
finding \(\theta \) using \(\arctan \left( {\frac{{\sqrt 7 }}{3}} \right)\) M1
\(\theta = \arctan \left( {\frac{{\sqrt 7 }}{3}} \right) + \pi {\text{ or }}\theta = \arctan \left( { – \frac{{\sqrt 7 }}{3}} \right) + \pi \) A1
\( \Rightarrow z = 2{{\text{e}}^{{\text{i}}\left( {\arctan \left( {\frac{{\sqrt 7 }}{3}} \right) + \pi } \right)}}{\text{ or}} \Rightarrow z = 2{{\text{e}}^{{\text{i}}\left( {\arctan \left( {\frac{{ – \sqrt 7 }}{3}} \right) + \pi } \right)}}\) A1
Note: Accept arguments in the range \( – \pi {\text{ to }}\pi {\text{ or }}0{\text{ to }}2\pi \) .
Accept answers in degrees.
[6 marks]
Question
The quadratic equation \({x^2} – 2kx + (k – 1) = 0\) has roots \(\alpha \) and \(\beta \) such that \({\alpha ^2} + {\beta ^2} = 4\). Without solving the equation, find the possible values of the real number \(k\).
▶️Answer/Explanation
Markscheme
\(\alpha + \beta = 2k\) A1
\(\alpha \beta = k – 1\) A1
\({(\alpha + \beta )^2} = 4{k^2} \Rightarrow {\alpha ^2} + {\beta ^2} + 2\underbrace {\alpha \beta }_{k – 1} = 4{k^2}\) (M1)
\({\alpha ^2} + {\beta ^2} = 4{k^2} – 2k + 2\)
\({\alpha ^2} + {\beta ^2} = 4 \Rightarrow 4{k^2} – 2k – 2 = 0\) A1
attempt to solve quadratic (M1)
\(k = 1,{\text{ }} – \frac{1}{2}\) A1
[6 marks]
Question
Sketch the graphs of \(y = \frac{x}{2} + 1\) and \(y = \left| {x – 2} \right|\) on the following axes.
 [3]
[3]
Solve the equation \(\frac{x}{2} + 1 = \left| {x – 2} \right|\).[4]
▶️Answer/Explanation
Markscheme
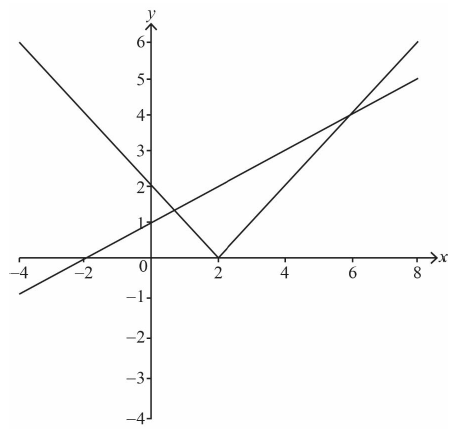
straight line graph with correct axis intercepts A1
modulus graph: V shape in upper half plane A1
modulus graph having correct vertex and y-intercept A1
[3 marks]
METHOD 1
attempt to solve \(\frac{x}{2} + 1 = x – 2\) (M1)
\(x = 6\) A1
Note: Accept \(x = 6\) using the graph.
attempt to solve (algebraically) \(\frac{x}{2} + 1 = 2 – x\) M1
\(x = \frac{2}{3}\) A1
[4 marks]
METHOD 2
\({\left( {\frac{x}{2} + 1} \right)^2} = {\left( {x – 2} \right)^2}\) M1
\(\frac{{{x^2}}}{4} + x + 1 = {x^2} – 4x + 4\)
\(0 = \frac{{3{x^2}}}{4} – 5x + 3\)
\(3{x^2} – 20x + 12 = 0\)
attempt to factorise (or equivalent) M1
\(\left( {3x – 2} \right)\left( {x – 6} \right) = 0\)
\(x = \frac{2}{3}\) A1
\(x = 6\) A1
[4 marks]