Question
In the triangle ABC, \({\rm{A\hat BC}} = 90^\circ\) , \({\text{AC}} = \sqrt {\text{2}}\) and AB = BC + 1.
a.Show that cos \(\hat A – \sin \hat A = \frac{1}{{\sqrt 2 }}\). [3]
b.By squaring both sides of the equation in part (a), solve the equation to find the angles in the triangle. [8]
c.Apply Pythagoras’ theorem in the triangle ABC to find BC, and hence show that \(\sin \hat A = \frac{{\sqrt 6 – \sqrt 2 }}{4}\). [6]
d. Hence, or otherwise, calculate the length of the perpendicular from B to [AC]. [4]
▶️Answer/Explanation
Markscheme
a.\(\cos \hat A = \frac{{{\text{BA}}}}{{\sqrt 2 }}\) A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }}\) A1
\(\cos \hat A – \sin \hat A = \frac{{{\text{BA}} – {\text{BC}}}}{{\sqrt 2 }}\) R1
\( = \frac{1}{{\sqrt 2 }}\) AG
[3 marks]
\({\cos ^2}\hat A – 2\cos \hat A\sin \hat A + {\sin ^2}\hat A = \frac{1}{2}\) M1A1
\(1 – 2\sin \hat A\cos \hat A = \frac{1}{2}\) M1A1
\(\sin 2\hat A = \frac{1}{2}\) M1
\(2\hat A = 30^\circ \) A1
angles in the triangle are 15° and 75° A1A1
Note: Accept answers in radians.
[8 marks]
\({\text{B}}{{\text{C}}^2} + {({\text{BC}} + 1)^2} = 2\) M1A1
\(2{\text{B}}{{\text{C}}^2} + 2{\text{BC}} – 1 = 0\) A1
\({\text{BC}} = \frac{{ -2 + \sqrt {12} }}{4}\left( { = \frac{{\sqrt 3 – 1}}{2}} \right)\) M1A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }} = \frac{{\sqrt 3 – 1}}{{2\sqrt 2 }}\) A1
\( = \frac{{\sqrt 6 – \sqrt 2 }}{4}\) AG
[6 marks]
EITHER
\(h = {\text{ABsin}}\hat A\) M1
\( = ({\text{BC}} + 1)\sin \hat A\) A1
\( = \frac{{\sqrt 3 + 1}}{2} \times \frac{{\sqrt 6 – \sqrt 2 }}{4} = \frac{{\sqrt 2 }}{4}\) M1A1
OR
\(\tfrac{1}{2}AB.BC = \tfrac{1}{2}AC.h\) M1
\(\frac{{\sqrt 3 – 1}}{2} \cdot \frac{{\sqrt {3 + 1} }}{2} = \sqrt {2h} \) A1
\(\frac{2}{4} = \sqrt 2 h\) M1
\(h = \frac{1}{{2\sqrt 2 }}\) A1
[4 marks]
Question
In the triangle ABC, \({\rm{A\hat BC}} = 90^\circ\) , \({\text{AC}} = \sqrt {\text{2}}\) and AB = BC + 1.
a.Show that cos \(\hat A – \sin \hat A = \frac{1}{{\sqrt 2 }}\). [3]
b.By squaring both sides of the equation in part (a), solve the equation to find the angles in the triangle. [8]
c.Apply Pythagoras’ theorem in the triangle ABC to find BC, and hence show that \(\sin \hat A = \frac{{\sqrt 6 – \sqrt 2 }}{4}\). [6]
d.Hence, or otherwise, calculate the length of the perpendicular from B to [AC]. [4]
▶️Answer/Explanation
Markscheme
a. \(\cos \hat A = \frac{{{\text{BA}}}}{{\sqrt 2 }}\) A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }}\) A1
\(\cos \hat A – \sin \hat A = \frac{{{\text{BA}} – {\text{BC}}}}{{\sqrt 2 }}\) R1
\( = \frac{1}{{\sqrt 2 }}\) AG
[3 marks]
\({\cos ^2}\hat A – 2\cos \hat A\sin \hat A + {\sin ^2}\hat A = \frac{1}{2}\) M1A1
\(1 – 2\sin \hat A\cos \hat A = \frac{1}{2}\) M1A1
\(\sin 2\hat A = \frac{1}{2}\) M1
\(2\hat A = 30^\circ \) A1
angles in the triangle are 15° and 75° A1A1
Note: Accept answers in radians.
[8 marks]
\({\text{B}}{{\text{C}}^2} + {({\text{BC}} + 1)^2} = 2\) M1A1
\(2{\text{B}}{{\text{C}}^2} + 2{\text{BC}} – 1 = 0\) A1
\({\text{BC}} = \frac{{ -2 + \sqrt {12} }}{4}\left( { = \frac{{\sqrt 3 – 1}}{2}} \right)\) M1A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }} = \frac{{\sqrt 3 – 1}}{{2\sqrt 2 }}\) A1
\( = \frac{{\sqrt 6 – \sqrt 2 }}{4}\) AG
[6 marks]
EITHER
\(h = {\text{ABsin}}\hat A\) M1
\( = ({\text{BC}} + 1)\sin \hat A\) A1
\( = \frac{{\sqrt 3 + 1}}{2} \times \frac{{\sqrt 6 – \sqrt 2 }}{4} = \frac{{\sqrt 2 }}{4}\) M1A1
OR
\(\tfrac{1}{2}AB.BC = \tfrac{1}{2}AC.h\) M1
\(\frac{{\sqrt 3 – 1}}{2} \cdot \frac{{\sqrt {3 + 1} }}{2} = \sqrt {2h} \) A1
\(\frac{2}{4} = \sqrt 2 h\) M1
\(h = \frac{1}{{2\sqrt 2 }}\) A1
[4 marks]
Question
Show that \(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\) .
▶️Answer/Explanation
Markscheme
METHOD 1
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\)
consider right hand side
\(\sec 2A + \tan 2A = \frac{1}{{\cos 2A}} + \frac{{\sin 2A}}{{\cos 2A}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for recognizing the need for single angles and A1 for recognizing \({\cos ^2}A + {\sin ^2}A = 1\) .
\( = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{\cos A + \sin A}}{{\cos A – \sin A}}\) AG
METHOD 2
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
\( = \frac{{1 + \sin 2A}}{{\cos 2A}}\) M1A1
\( = \sec 2A + \tan 2A\) AG
[6 marks]
Question
a. Show that \(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) for \(0 < \alpha < \frac{\pi }{2}\). [1]
b. Hence find \(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x,{\text{ }}0 < \alpha < \frac{\pi }{2}} \). [4]
▶️Answer/Explanation
Markscheme
EITHER
a.use of a diagram and trig ratios
eg,
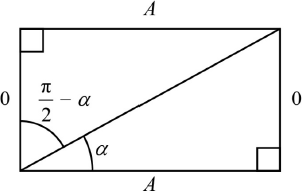
\(\tan \alpha = \frac{O}{A} \Rightarrow \cot \alpha = \frac{A}{O}\)
from diagram, \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{A}{O}\) R1
OR
use of \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} – \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} – \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) R1
THEN
\(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) AG
[1 mark]
\(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x} = [\arctan x]_{\tan \alpha }^{\cot \alpha }\) (A1)
Note: Limits (or absence of such) may be ignored at this stage.
\( = \arctan (\cot \alpha ) – \arctan (\tan \alpha )\) (M1)
\( = \frac{\pi }{2} – \alpha – \alpha \) (A1)
\( = \frac{\pi }{2} – 2\alpha \) A1
[4 marks]
Question
Given that \(sin(x+\frac{\pi}{3})=2cos(x-\frac{\pi}{6})\), find the values of tan x, cot x and cos x.
▶️Answer/Explanation
Ans
\(sin(x+\frac{\pi}{3})=2cons(x-\frac{\pi}{6} \Rightarrow sin x cos\frac{\po}{3}+sin\frac{\pi}{3}cos x=2(cosxcox\frac{\pi}{6}+sinxsin\frac{\pi}{6}\)
\(\Rightarrow \frac{1}{2}sinxcos\frac{\pi}{3}+\frac{\sqrt{3}}{2}cosx=2(\frac{\sqrt{3}}{2}cosx+\frac{1}{2}sinx)\)
\(\Rightarrow sinx +\sqrt{3}cos x =2\sqrt{3}cos x+2sinx\)
\(\Rightarrow -sinx =\sqrt{3}cosx\Rightarrow tanx =-\sqrt{3}\)
\(ctx=-\frac{1}{\sqrt{3}}\)
\(tan^2x+1=\frac{1}{cos^2x}\Rightarrow cos^2x=\frac{1}{4}\Rightarrow tan x =-\sqrt{3}\)
(indeed, the original equations has solution \(-\frac{\pi}{3}+2k\pi,\frac{2\pi}{3}+2k\pi \) and hence \(cos x = \pm \frac{1}{2})\)