Question
In triangle ABC, AB = 9 cm , AC = 12 cm , and \(\hat B\) is twice the size of \({\hat C}\) .
Find the cosine of \({\hat C}\) .
▶️Answer/Explanation
Markscheme
\(\frac{9}{{\sin C}} = \frac{{12}}{{\sin B}}\) (M1)
\(\frac{9}{{\sin C}} = \frac{{12}}{{\sin 2C}}\) A1
Using double angle formula \(\frac{9}{{\sin C}} = \frac{{12}}{{2\sin C\cos C}}\) M1
\( \Rightarrow 9(2\sin C\cos C) = 12\sin C\)
\( \Rightarrow 6\sin C(3\cos C – 2) = 0\,\,\,\,\,{\text{or equivalent}}\) (A1)
\((\sin C \ne 0)\)
\( \Rightarrow \cos C = \frac{2}{3}\) A1
[5 marks]
Question
In the triangle PQR, PQ = 6 , PR = k and \({\rm{P\hat QR}} = 30^\circ \) .
a.For the case k = 4 , find the two possible values of QR.[4]
b.Determine the values of k for which the conditions above define a unique triangle.[3]
▶️Answer/Explanation
Markscheme
attempt to apply cosine rule M1
\({4^2} = {6^2} + {\text{Q}}{{\text{R}}^2} – 2 \cdot {\text{QR}} \cdot 6\cos 30^\circ\) ( or \({\text{Q}}{{\text{R}}^2} – 6\sqrt 3 {\text{ QR}} + 20 = 0\) ) A1
\({\text{QR}} = 3\sqrt 3 + \sqrt 7 {\text{ or QR}} = 3\sqrt 3 – \sqrt 7 \) A1A1
[4 marks]
METHOD 1
\(k \geqslant 6\) A1
\(k = 6\sin 30^\circ = 3\) M1A1
Note: The M1 in (b) is for recognizing the right-angled triangle case.
METHOD 2
\(k \geqslant 6\) A1
use of discriminant: \(108 – 4(36 – {k^2}) = 0\) M1
k = 3 A1
Note: k = ±3 is M1A0.
[3 marks]
Question
In triangle \({\text{ABC, BC}} = \sqrt 3 {\text{ cm}}\), \({\rm{A\hat BC}} = \theta \) and \({\rm{B\hat CA}} = \frac{\pi }{3}\).
a.Show that length \({\text{AB}} = \frac{3}{{\sqrt 3 \cos \theta + \sin \theta }}\).[4]
b.Given that \(AB\) has a minimum value, determine the value of \(\theta \) for which this occurs.[4]
▶️Answer/Explanation
Markscheme
any attempt to use sine rule M1
\(\frac{{{\text{AB}}}}{{\sin \frac{\pi }{3}}} = \frac{{\sqrt 3 }}{{\sin \left( {\frac{{2\pi }}{3} – \theta } \right)}}\) A1
\( = \frac{{\sqrt 3 }}{{\sin \frac{{2\pi }}{3}\cos \theta – \cos \frac{{2\pi }}{3}\sin \theta }}\) A1
Note: Condone use of degrees.
\( = \frac{{\sqrt 3 }}{{\frac{{\sqrt 3 }}{2}\cos \theta + \frac{1}{2}\sin \theta }}\) A1
\(\frac{{{\text{AB}}}}{{\frac{{\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{{\frac{{\sqrt 3 }}{2}\cos \theta + \frac{1}{2}\sin \theta }}\)
\(\therefore {\text{AB}} = \frac{3}{{\sqrt 3 \cos \theta + \sin \theta }}\) AG
[4 marks]
METHOD 1
\(({\text{AB}})’ = \frac{{ – 3\left( { – \sqrt 3 \sin \theta + \cos \theta } \right)}}{{{{\left( {\sqrt 3 \cos \theta + \sin \theta } \right)}^2}}}\) M1A1
setting \(({\text{AB}})’ = 0\) M1
\(\tan \theta = \frac{1}{{\sqrt 3 }}\)
\(\theta = \frac{\pi }{6}\) A1
METHOD 2
\({\text{AB}} = \frac{{\sqrt 3 \sin \frac{\pi }{3}}}{{\sin \left( {\frac{{2\pi }}{3} – \theta } \right)}}\)
\(AB\) minimum when \(\sin \left( {\frac{{2\pi }}{3} – \theta } \right)\) is maximum M1
\(\sin \left( {\frac{{2\pi }}{3} – \theta } \right) = 1\) (A1)
\(\frac{{2\pi }}{3} – \theta = \frac{\pi }{2}\) M1
\(\theta = \frac{\pi }{6}\) A1
METHOD 3
shortest distance from \(B\) to \(AC\) is perpendicular to \(AC\) R1
\(\theta = \frac{\pi }{2} – \frac{\pi }{3} = \frac{\pi }{6}\) M1A2
[4 marks]
Total [8 marks]
Question
The following diagram shows the triangle ABC where \({\text{AB}} = 2,{\text{ AC}} = \sqrt 2 \) and \({\rm{B\hat AC}} = 15^\circ \).
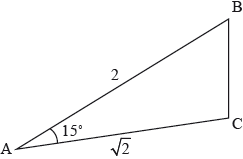
a.Expand and simplify \({\left( {1 – \sqrt 3 } \right)^2}\).[1]
b.By writing \(15^\circ \) as \(60^\circ – 45^\circ \) find the value of \(\cos (15^\circ )\).[3]
c.Find BC in the form \(a + \sqrt b \) where \(a,{\text{ }}b \in \mathbb{Z}\).[4]
▶️Answer/Explanation
Markscheme
\({\left( {1 – \sqrt 3 } \right)^2} = 4 – 2\sqrt 3 \) A1
Note: Award A0 for \(1 – 2\sqrt 3 + 3\).
[1 mark]
\(\cos (60^\circ – 45^\circ ) = \cos (60^\circ )\cos (45^\circ ) + \sin (60^\circ )\sin (45^\circ )\) M1
\( = \frac{1}{2} \times \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 2 }}{2}{\text{ }}\left( {{\text{or }}\frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}} \right)\) (A1)
\( = \frac{{\sqrt 2 + \sqrt 6 }}{4}{\text{ }}\left( {{\text{or }}\frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}} \right)\) A1
[3 marks]
\(B{C^2} = 2 + 4 – 2 \times \sqrt 2 \times 2\cos (15^\circ )\) M1
\( = 6 – \sqrt 2 \left( {\sqrt 2 + \sqrt 6 } \right)\)
\( = 4 – \sqrt {12} {\text{ }}\left( { = 4 – 2\sqrt 3 } \right)\) A1
\(BC = \pm \left( {1 – \sqrt 3 } \right)\) (M1)
\(BC = – 1 + \sqrt 3 \) A1
Note: Accept \(BC = \sqrt 3 – 1\).
Note: Award M1A0 for \(1 – \sqrt 3 \).
Note: Valid geometrical methods may be seen.
[4 marks]