Question
In the diagram below, [AB] is a diameter of the circle with centre O. Point C is on the circumference of the circle. Let \(\overrightarrow {{\text{OB}}} = \boldsymbol{b} \) and \(\overrightarrow {{\text{OC}}} = \boldsymbol{c}\) .
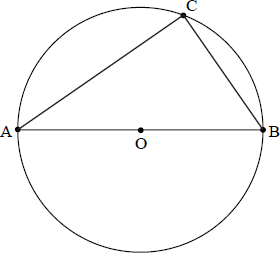
Find an expression for \(\overrightarrow {{\text{CB}}} \) and for \(\overrightarrow {{\text{AC}}} \) in terms of \(\boldsymbol{b}\) and \(\boldsymbol{c}\) .
Hence prove that \({\rm{A\hat CB}}\) is a right angle.
Answer/Explanation
Markscheme
\(\overrightarrow {{\text{CB}}} = \boldsymbol{b} – \boldsymbol{c}\) , \(\overrightarrow {{\text{AC}}} = \boldsymbol{b} + \boldsymbol{c}\) A1A1
Note: Condone absence of vector notation in (a).
[2 marks]
\(\overrightarrow {{\text{AC}}} \cdot \overrightarrow {{\text{CB}}} = \)(b + c)\( \cdot \)(b – c) M1
= \(|\)b\({|^2}\) – \(|\)c\({|^2}\) A1
= 0 since \(|\)b\(|\) = \(|\)c\(|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AC}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\rm{A\hat CB}}\) is a right angle AG
[3 marks]
Examiners report
Most candidates were able to find the expressions for the two vectors although a number were not able to do this. Most then tried to use Pythagoras’ theorem and confused scalars and vectors. There were few correct responses to the second part. Candidates did not seem to be able to use the algebra of vectors comfortably.
Most candidates were able to find the expressions for the two vectors although a number were not able to do this. Most then tried to use Pythagoras’ theorem and confused scalars and vectors. There were few correct responses to the second part. Candidates did not seem to be able to use the algebra of vectors comfortably.