Question
Two submarines A and B have their routes planned so that their positions at time t hours, 0 ≤ t < 20 , would be defined by the position vectors rA 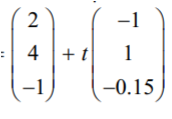 and
and 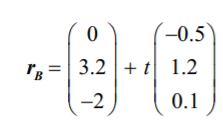 relative to a fixed point on the surface of the ocean (all lengths are in kilometres).
relative to a fixed point on the surface of the ocean (all lengths are in kilometres).
To avoid the collision submarine B adjusts its velocity so that its position vector is now given by

a. Show that the two submarines would collide at a point P and write down the coordinates of P.[4]
b.i.Show that submarine B travels in the same direction as originally planned.[1]
b.ii. Find the value of t when submarine B passes through P.[2]
c.i. Find an expression for the distance between the two submarines in terms of t.[5]
c.ii. Find the value of t when the two submarines are closest together.[2]
c.iii. Find the distance between the two submarines at this time.[1]
▶️Answer/Explanation
Markscheme
rA = rB (M1)
2 − t = − 0.5t ⇒ t = 4 A1
checking t = 4 satisfies 4 + t = 3.2 + 1.2t and − 1 − 0.15t = − 2 + 0.1t R1
P(−2, 8, −1.6) A1
Note: Do not award final A1 if answer given as column vector.
[4 marks]
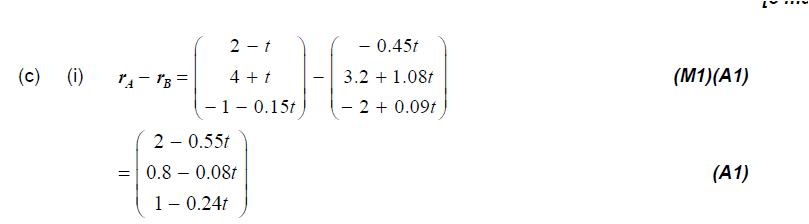

Note: Accept rA − rB.
distance \(D = \sqrt {{{\left( {2 – 0.55t} \right)}^2} + {{\left( {0.8 – 0.08t} \right)}^2} + {{\left( {1 – 0.24t} \right)}^2}} \) M1A1
\(\left( { = \sqrt {8.64 – 2.688t + 0.317{t^2}} } \right)\)
[5 marks]
minimum when \(\frac{{{\text{d}}D}}{{{\text{d}}t}} = 0\) (M1)
t = 3.83 A1
[2 marks]
0.511 (km) A1
[1 mark]