IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 10.1 Describing fields
Topic 10 Weightage : 5 %
All Questions for Topic 10.1 – Gravitational fields , Electrostatic fields , Electric potential and gravitational potential , Field lines , Equipotential surfaces
Question
Which is a correct unit for gravitational potential?
A 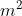
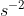
B J kg
C m 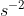
D N 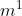
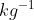
▶️Answer/Explanation
Ans: A
GRAVITATIONAL POTENTIAL
Question
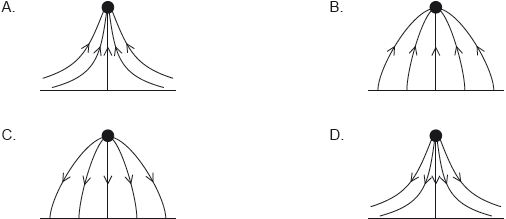
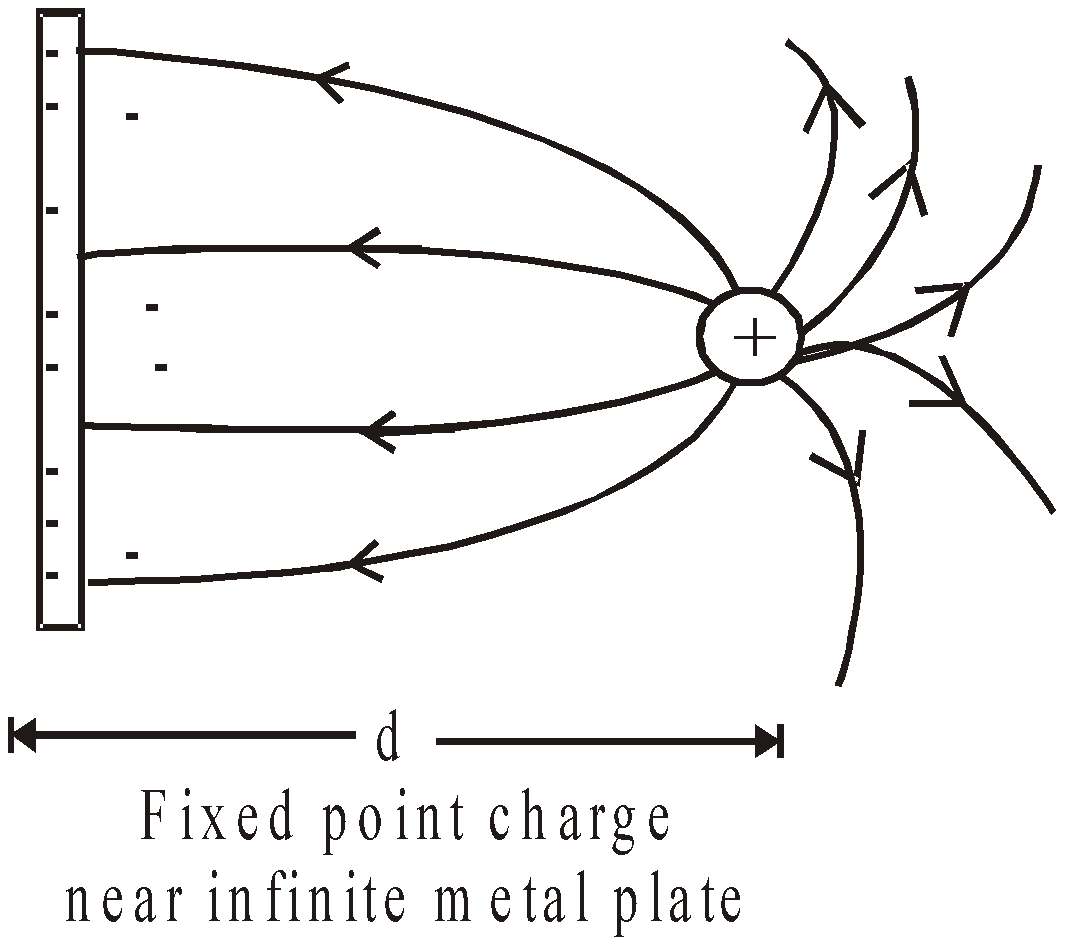
A positive point charge is placed above a metal plate at zero electric potential. Which diagram shows the pattern of electric field lines between the charge and the plate?
▶️Answer/Explanation
Markscheme
C
Electric lines of force generate or terminate at charges /surfaces at right angles. Positive charge induce a negative charge towards it positive charge on other side of plate.
Question
The diagram shows the electric field and the electric equipotential surfaces between two charged parallel plates. The potential difference between the plates is 200 V.
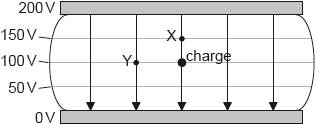
What is the work done, in nJ, by the electric field in moving a negative charge of magnitude 1 nC from the position shown to X and to Y?
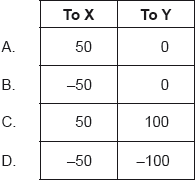
▶️Answer/Explanation
Markscheme
A
\(W_{CX} =-10^{-9}\times 50 = -50 \; nJ\)
dU=-dW
or
\(dW = -(-50) = 50 \; nJ\)
Question
A moon of mass M orbits a planet of mass 100M. The radius of the planet is R and the distance between the centres of the planet and moon is 22R.

What is the distance from the centre of the planet at which the total gravitational potential has a maximum value?
A. 2R
B. 11R
C. 20R
D. 2R and 20R
▶️Answer/Explanation
Markscheme
C
Let the potential be maximum at point x from center of planet

Gravitational potential is given by
\(V_g=-\frac{G100M}{x}-\frac{GM}{22-x}\)
now \(V_g\) to be maximum \(\frac{dV_g}{dx}=0\)
or
\(\frac{d}{dx}(-\frac{G100M}{x}-\frac{GM}{22-x})=0\)
or
\(\frac{d}{dx}(-\frac{100}{x}-\frac{1}{22-x})=0\)
or
\(\frac{100}{x^2}-\frac{1}{(22-x)^{2}}=0\)
\(100 \times (22-x)^2=x^2\)
or
\(10 \times (22-x) =x\)
\(220 – 10x =x\)
\(11 x =220\)
\(x = 20\)
Question
The diagram shows 5 gravitational equipotential lines. The gravitational potential on each line is indicated. A point mass m is placed on the middle line and is then released. Values given in MJ kg–1.

Which is correct about the direction of motion and the acceleration of the point mass?
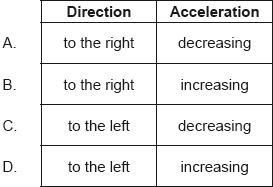
▶️Answer/Explanation
Markscheme
D
we have relation in force and potential as
\(F= -\frac{dU}{dx}=-\frac{\Delta U}{\Delta x}=\frac{U_1-U_2}{x_2-x_1}\)
Hence we can see gravitational force will be towards left and this will cause acceleration of the point mass
Question
Four identical, positive, point charges of magnitude Q are placed at the vertices of a square of side 2d. What is the electric potential produced at the centre of the square by the four charges?
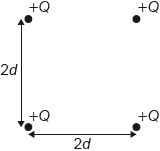
A. 0
B. \(\frac{{4kQ}}{d}\)
C. \(\frac{{\sqrt 2 kQ}}{d}\)
D. \(\frac{{2\sqrt 2 kQ}}{d}\)
▶️Answer/Explanation
Markscheme
D
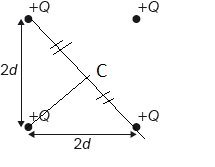
All four charges are equidistance from center square.
Hence distance for each charge \(= \frac{\sqrt{(2d)^2+(2d)^2}}{2}=\sqrt{2}d\)
potential due to a charge Q at distance \( \sqrt{2}d\) is
\(V_{p1} =k\frac{Q}{\sqrt{2}d}\)
Hence due to all four charge
\(4 \times V_{p1} \) all four charges are same and equidistance from center
\(\therefore V_p = 4 \times V_{p1} = 4 \times k\frac{Q}{\sqrt{2}d}\)
\(=\frac{2\sqrt{2} kQ}{d}\)