IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 10.1 Describing fields
Topic 10 Weightage : 5 %
All Questions for Topic 10.1 – Gravitational fields , Electrostatic fields , Electric potential and gravitational potential , Field lines , Equipotential surfaces
Question
The diagram shows the electric field lines of a positively charged conducting sphere of radius
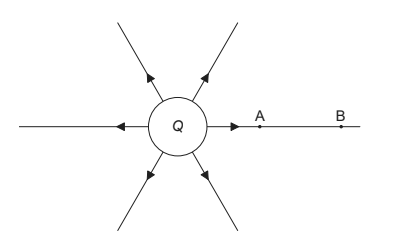
Points A and B are located on the same field line.
(a) Explain why the electric potential decreases from A to B. [2]
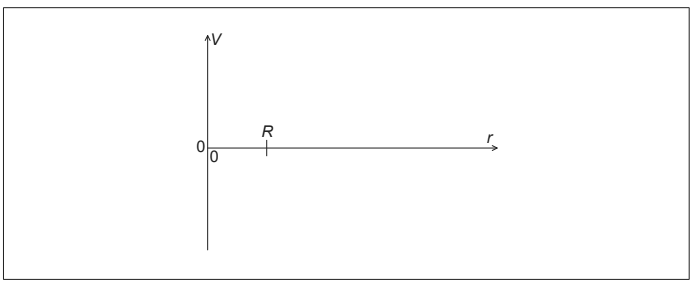
(b) Draw, on the axes, the variation of electric potential V with distance r from the centre of the sphere. [2]
(c) The concept of potential is also used in the context of gravitational fields. Suggest why scientists developed a common terminology to describe different types of fields. [1]
▶️Answer/Explanation
Ans:
a.
ALTERNATIVE 1
work done on moving a positive test charge in any outward direction is negative ✓
potential difference is proportional to this work «so V decreases from A to B» ✓
ALTERNATIVE 2
potential gradient is directed opposite to the field so inwards ✓
the gradient indicates the direction of increase of V «hence V increases towards the
centre/decreases from A to B» ✓
ALTERNATIVE 3
V = \(\frac{KQ}{R}\)
so as r increases V decreases ✓
V is positive as Q is positive ✓
ALTERNATIVE 4
the work done per unit charge in bringing a positive charge from infinity ✓
to point B is less than point A ✓
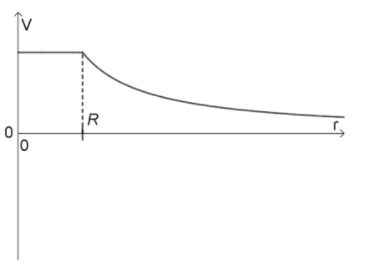
b
curve decreasing asymptotically for r > R
non – zero constant between 0 and R
c to highlight similarities between «different» fields
A planet has radius R. At a distance h above the surface of the planet the gravitational field strength is g and the gravitational potential is V.
a.i.State what is meant by gravitational field strength.[1]

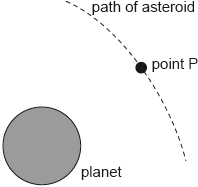
When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b). [3]
▶️Answer/Explanation
Markscheme
a.i.
the «gravitational» force per unit mass exerted on a point/small/test mass
[1 mark]
at height h potential is V = –\(\frac{{GM}}{{(R + h)}}\)
field is g = \(\frac{{GM}}{{{{(R + h)}^2}}}\)
«dividing gives answer»
Do not allow an answer that starts with g = –\(\frac{{\Delta V}}{{\Delta r}}\) and then cancels the deltas and substitutes R + h
[2 marks]
correct shape and sign
non-zero negative vertical intercept
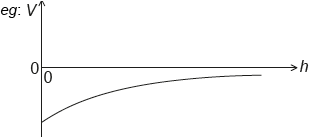
[2 marks]
V = «–2.2 × (3.1 × 106 + 2.4 × 107) =» «–» 6.0 × 107 J kg–1
Unit is essential
Allow eg MJ kg–1 if power of 10 is correct
Allow other correct SI units eg m2s–2, N m kg–1
[1 mark]
total energy at P = 0 / KE gained = GPE lost
«\(\frac{1}{2}\)mv2 + mV = 0 ⇒» v = \(\sqrt { – 2V} \)
v = «\(\sqrt {2 \times 6.0 \times {{10}^7}} \) =» 1.1 × 104 «ms–1»
Award [3] for a bald correct answer
Ignore negative sign errors in the workings
Allow ECF from 6(b)
[3 marks]
ALTERNATIVE 1
force on asteroid is «6.2 × 1012 × 2.2 =» 1.4 × 1013 «N»
«by Newton’s third law» this is also the force on the planet
ALTERNATIVE 2
mass of planet = 2.4 x 1025 «kg» «from V = –\(\frac{{GM}}{{(R + h)}}\)»
force on planet «\(\frac{{GMm}}{{{{(R + h)}^2}}}\)» = 1.4 × 1013 «N»
MP2 must be explicit
[2 marks]