This question is in two parts. Part 1 is about energy resources. Part 2 is about electric fields.
Part 1 Energy resources
A photovoltaic panel is made up of a collection (array) of photovoltaic cells. The panel has a total area of \({\text{1.3 }}{{\text{m}}^{\text{2}}}\) and is mounted on the roof of a house. The maximum intensity of solar radiation at the location of the panel is \({\text{750 W}}\,{{\text{m}}^{ – 2}}\). The panel produces a power output of 210 W when the solar radiation is at its maximum intensity.
The owner of the house chooses between photovoltaic panels and solar heating panels to provide 4.2 kW of power to heat water. The solar heating panels have an efficiency of 70%. The maximum intensity of solar radiation at the location remains at \({\text{750 W}}\,{{\text{m}}^{ – 2}}\).
Part 2 Electric fields
An isolated metal sphere is placed in a vacuum. The sphere has a negative charge of magnitude 12 nC.

Outside the sphere, the electric field strength is equivalent to that of a point negative charge of magnitude 12 nC placed at the centre of the sphere. The radius \(r\) of the sphere is 25 mm.
An electron is initially at rest on the surface of the sphere.
a.
The Sun is a renewable energy source whereas a fossil fuel is a non-renewable energy source. Outline the difference between renewable and non-renewable energy sources.[2]
With reference to the energy transformations and the operation of the devices, distinguish between a photovoltaic cell and a solar heating panel.[2]
Determine the efficiency of the photovoltaic panel.[2]
State two reasons why the intensity of solar radiation at the location of the panel is not constant.
1.
2.[2]
Calculate the minimum area of solar heating panel required to provide this power.[2]
Comment on whether it is better to use a solar heating panel rather than an array of photovoltaic panels for the house. Do not consider the installation cost of the panels in your answer.[2]
Using the diagram, draw the electric field pattern due to the charged sphere.[2]
Show that the magnitude of the electric field strength at the surface of the sphere is about \(2 \times {10^5}{\text{ N}}\,{{\text{C}}^{ – 1}}\).[2]
On the axes, draw a graph to show the variation of the electric field strength \(E\) with distance \(d\) from the centre of the sphere.
 [2]
[2]
Calculate the initial acceleration of the electron.[2]
Discuss the subsequent motion of the electron.[2]
Answer/Explanation
Markscheme
a.
renewable sources:
rate of use/depletion of energy source;
is less than rate of production/regeneration of source;
Accept equivalent statement for non-renewable sources.
or
mention of rate of production / usage;
comparison of sources in terms of being used up/depleted/lasting a long time etc;
Award [1] if answer makes clear the difference but does not address the rate of production.
solar heating panel converts solar/radiation/photon/light energy into thermal/heat energy and photovoltaic cell converts solar/radiation/photon/light energy into electrical energy; } (both needed)
in solar heating hot liquid is stored/circulated and photovoltaic cell generates emf/pd; } (both needed)
(power available at roof) \( = 1.3 \times 750{\text{ }}( = 975{\text{ W}})\);
efficiency \( = \left( {\frac{{210}}{{975}} = } \right){\text{ }}0.22\)\(\,\,\,\)or\(\,\,\,\)22%;
depends on time of day;
depends of time of year;
depends on weather (eg cloud cover) at location;
power output of Sun varies;
Earth-Sun distance varies;
area of panel \( = \frac{{4200}}{{0.7 \times 750}}\);
\({\text{8 }}{{\text{m}}^{\text{2}}}\);
calculates area of photovoltaic panels needed as about \({\text{26 }}{{\text{m}}^{\text{2}}}\) / makes a quantitative comparison;
solar heating takes up less area/more efficient/faster;
further energy conversion needed, from electrical to thermal, with photovoltaic panels, involving further losses / OWTTE;
Allow ECF from (d)(i) with appropriate reverse argument.
radial field with arrows and direction correct towards the sphere; (both needed)
no field inside sphere;
At least four lines of force to be shown on diagram.
use of \(E = \frac{{kQ}}{{{r^2}}}\);
\(1.73 \times {10^5}{\text{ N}}\,{{\text{C}}^{ – 1}}\); (must see answer to 2+ significant figures)
line drawn showing zero field strength inside sphere;
decreasing in inverse square-like way from a value of \(2 \times {10^5}{\text{ N}}\,{{\text{C}}^{ – 1}}\)\(\,\,\,\)or\(\,\,\,\)\(1.7 \times {10^5}{\text{ N}}\,{{\text{C}}^{ – 1}}\) at the surface, \(d = 25{\text{ mm}}\);
force \( = 1.7 \times {10^5} \times 1.6 \times {10^{ – 19}}\); (allow use of \(2 \times {10^5}{\text{ N}}{{\text{C}}^{ – 1}}\))
acceleration \( = \left( {\frac{{2.7 \times {{10}^{ – 14}}}}{{9.1 \times {{10}^{ – 31}}}} = } \right){\text{ }}3.0 \times {10^{16}}{\text{ m}}\,{{\text{s}}^{ – 2}}\);
radially away from sphere / away from centre of sphere;
velocity increasing but at a decreasing rate / accelerating with decreasing acceleration;
because (electric) field (strength) is decreasing;
a.
Define electric field strength.[2]
The diagram shows a pair of horizontal metal plates. Electrons can be deflected vertically using an electric field between the plates.
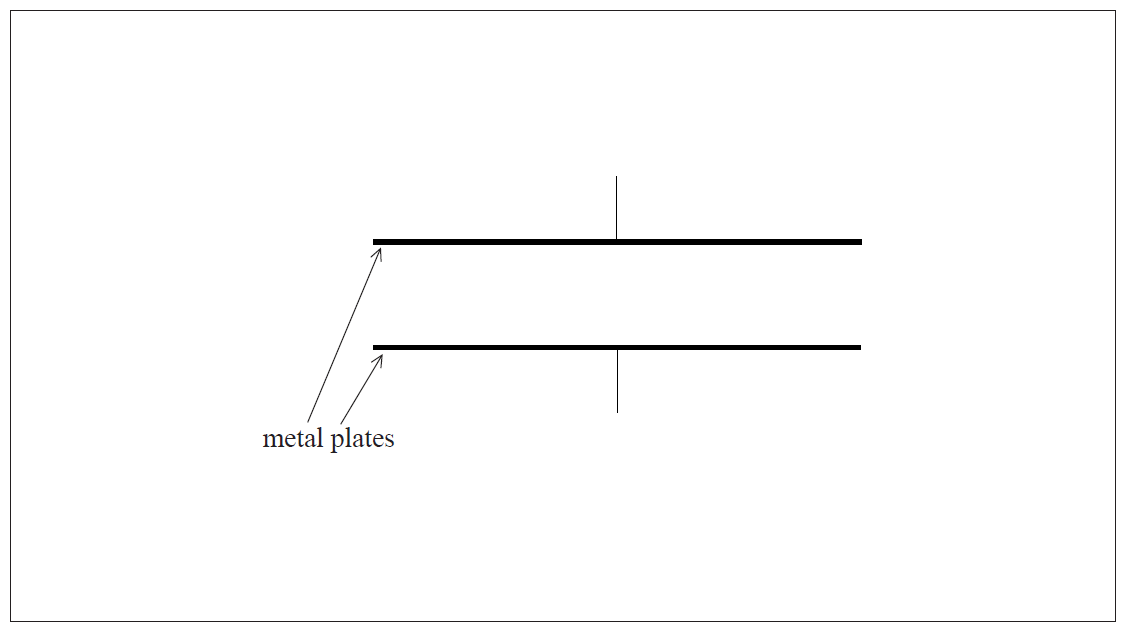
(i) Label, on the diagram, the polarity of the metal plates which would cause an electron
positioned between the plates to accelerate upwards.
(ii) Draw the shape and direction of the electric field between the plates on the diagram.
(iii) Calculate the force on an electron between the plates when the electric field strength has a value of 2.5 × 103 NC–1.[5]
The diagram shows two isolated electrons, X and Y, initially at rest in a vacuum. The initial separation of the electrons is 5.0 mm. The electrons subsequently move apart in the directions shown.

(i) Show that the initial electric force acting on each electron due to the other electron is approximately 9 × 10–24N.
(ii) Calculate the initial acceleration of one electron due to the force in (c)(i).
(iii) Discuss the motion of one electron after it begins to move.
(iv) The diagram shows Y as seen from X, at one instant. Y is moving into the plane of the paper. For this instant, draw on the diagram the shape and direction of the magnetic field produced by Y.
 [8]
[8]
Answer/Explanation
Markscheme
a.
force per unit charge;
on a positive test charge / on a positive small charge;
(i) top plate positive and bottom negative (or +/- and ground);
(ii) 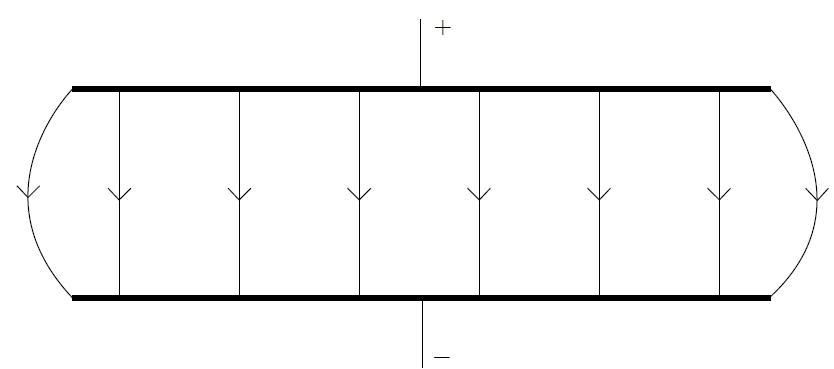
uniform (by eye) line spacing and edge effect, field lines touching both plates;
downward arrows (minimum of one and none upward);
(iii) F=2.5×103×1.6×10-19
4.0×10-16 (N);
Award [2] for a bald correct answer.
(i) use of \(F = \frac{{{{\left( {1.60 \times {{10}^{ – 19}}} \right)}^2}}}{{4\pi {\varepsilon _0}{{\left( {5.0 \times {{10}^{ – 3}}} \right)}^2}}}\) or \(F = \frac{{{{\left( {1.60 \times {{10}^{ – 19}}} \right)}^2}}}{{{{\left( {5.0 \times {{10}^{ – 3}}} \right)}^2}}} \times 8.99 \times {10^9}\);
9.2×10-24(N);
(ii) 1.0×107 (ms-2) (9.9×106 (ms-2) if 9×10-24 (N) used);
(iii) electron will continue to accelerate;
speed increases with acceleration;
acceleration reduces with separation;
when outside the field no further acceleration/constant speed;
any reference to accelerated charge radiating and losing (kinetic) energy;
(iv) minimum of two concentric circles centred on Y;
anti-clockwise;