IBDP Physics 11.1 – Electromagnetic induction: IB Style Question Bank HL Paper 1

IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics

Topic 11.1 Electromagnetic induction

Topic 11 Weightage : 5 %

All Questions for Topic 11.1 – Electromotive force (emf) , Magnetic flux and magnetic flux linkage , Faraday’s law of induction , Lenz’s law

Question

The conservation of which quantity explains Lenz’s law?

A Charge

B Energy

C Magnetic field

D Mass

▶️Answer/Explanation

Ans: B

LENZ’S LAW

The direction of induced e.m.f. is given by Lenz’s law. According to this law, the direction of induced e.m.f. in a circuit is always such that it opposes the every cause which produces it.

Thus,

Lenz’s law is in accordance with the principle of conservation of energy. Infact, work done in moving the magnet w.r.t. the coil changes into electric energy producing induced current.

Question

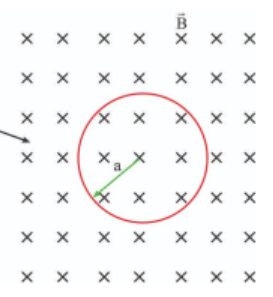
A conducting ring encloses an area of 2.0 cm² and is perpendicular to a magnetic field of strength 5.0 mT. The direction of the magnetic field is reversed in a time 4.0 s. What is the average emf induced in the ring?

A 0

B. 0.25 μV

C. 0.40μV

D. 0.50μV

▶️Answer/Explanation

Ans: D

Faraday’s Law of Induction

FARADAY’S LAW OF ELECTROMAGNETIC INDUCTION

Whenever the number of magnetic lines of force (flux) linked with any closed circuit change, an induced current flows through the circuit which lasts only so long as the change lasts. An increase in the number of lines of force produces an inverse current, while a decrease of such lines produces a direct current.

The induced emf is equal to the negative rate of change of magnetic flux.

i.e.

The -ve sign shows that the induced emf opposes the change in magnetic flux (Lenz’s law).

In the given question

\(\phi_1 = BA\)
\(\phi_2 = -BA\) ( as direction of B is reversed)
hence \(\Delta \phi = \phi_2 -\phi_1 =2BA\)
Time taken for \(\phi\) to change \(= 4 s\)
Hence
\(e =-\frac{\Delta \phi}{\Delta t} =-\frac{-2\times B \times A}{4}\)
\(=\frac{2\times 2 \times 10^{-4} \times 5 \times 10^{-3}}{4}=5\times 10^{-7} =0.5 \mu T\)

Question

A uniform magnetic field directed into the page occupies a region of width L. A conducting coil of width L moves at constant speed v, from left to right, through the field.

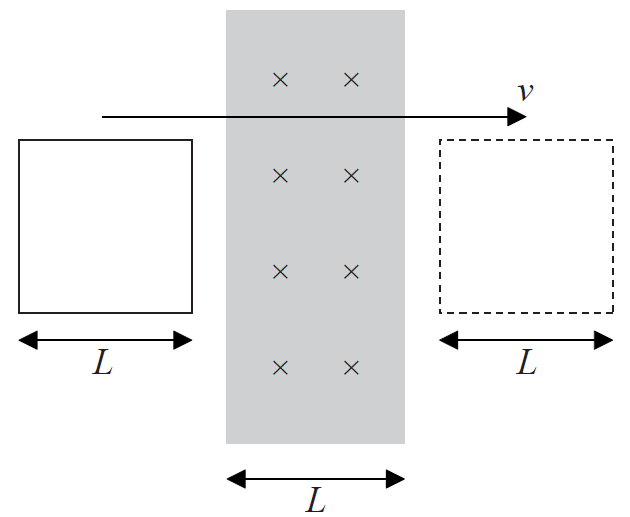
From the instant that the coil enters the field until the instant that the coil leaves the field, which of the following best describes the direction of the current induced in the coil?

A. Anti-clockwise

B. Clockwise

C. Anti-clockwise then clockwise

D. Clockwise then anti-clockwise

▶️Answer/Explanation

Markscheme

As the square is entering the field the flux linkage is increasing, while as it is leaving the linkage is decreasing. As per Lenz’s Law , direction of the current is such as to try to reduce the change in flux linkage.

Hence it should set up a magnetic field out of the page as the loop enters the field. and into the page when loop is leaving the magnetic field

Hence answer is C

Question

The current I flowing in loop A in a clockwise direction is increasing so as to induce a current both in loops B and C. All three loops are on the same plane.

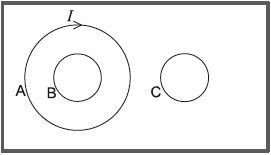
What is the direction of the induced currents in loop B and loop C?

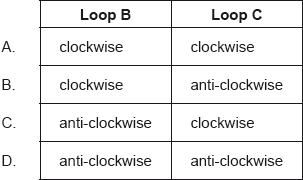
▶️Answer/Explanation

Markscheme

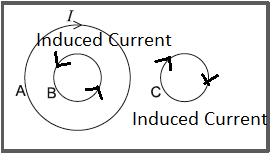
As per Lenz’s Law , direction of the current is such as to try to reduce the change in flux linkage. As current in circle A increases , this will increase linked flus to circle B and hence induced current will try to reduce this change and hence induced current will be in anti clock wise.

Similarly current goes downward near circle C , it will induced a current upward in circle C.

Question

A coil of area A is placed in a region of uniform horizontal magnetic field B. At t=0, the coil starts to rotate with constant angular speed ω about a horizontal axis.

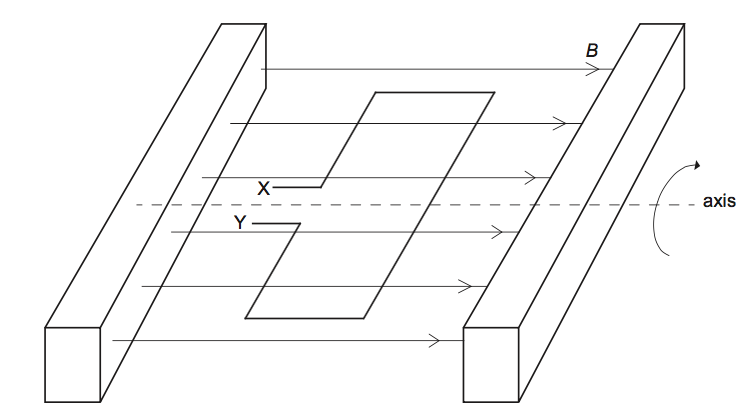
What is the emf between X and Y?

A. zero

B. ωAB sin ωt

C. AB cos ωt

D. −ωAB sin ωt

▶️Answer/Explanation

Markscheme

The number of magnetic lines of force crossing a surface is called magnetic flux linked with the surface. It is represented by

Magnetic flux \(\phi = \vec{B}. \vec{A} =\vec{B}. A\hat{n} =A(\vec{B}.\hat{n})\)

In given question

\(\theta = 90^{\circ}\)
Hence
\(cos\;90^{\circ} =0\)
or

\(\phi = BA cos\;90^{\circ} =0\)
hence

\(e =-\frac{d\phi}{dt} =0\)

Question

Faraday’s law of electromagnetic induction states that the electromotive force (emf) induced in a conductor is proportional to

A. the change of magnetic flux density.

B. the change of magnetic flux linkage.

C. the rate of change of magnetic flux density.

D. the rate of change of magnetic flux linkage.

▶️Answer/Explanation

Markscheme

FARADAY’S LAW OF ELECTROMAGNETIC INDUCTION

The induced emf is equal to the negative rate of change of magnetic flux.

i.e.

The -ve sign shows that the induced emf opposes the change in magnetic flux (Lenz’s law).

Question

The diagram shows a loop L of wire in a uniform magnetic field B.

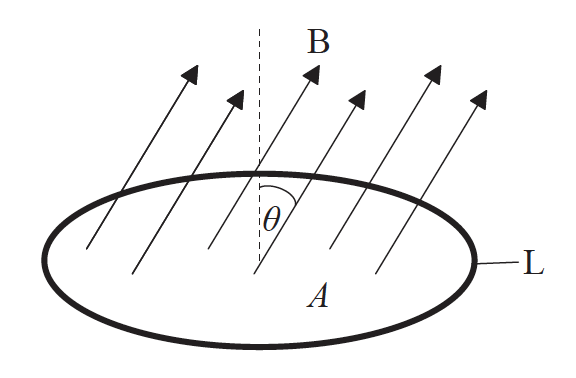
The loop encloses an area A and the field is directed at an angle θ to the normal to the plane of the loop. The strength of B is increasing at a uniform rate R. What is the emf induced in L?

A. \(\frac{{RA}}{{\cos \theta }}\)

B. RA cos θ

C. \(\frac{{RA}}{{\sin \theta }}\)

D. RA sin θ

▶️Answer/Explanation

Markscheme

\(\phi = BA cos\theta\)
hence \(e =-\frac{d\phi}{dt} =-\frac{d(BA cos\theta)}{dt} =-A cos \theta \frac{dB}{dt}\)
since \(\theta\) and Area \(A\) is constant
Hence
\(e =-A cos \theta \times R\)

Related Links

IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics

Question

Question

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Question

Markscheme

Need Help ? Book A Tutor