IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 12.2 Nuclear physics
Topic 12 Weightage : 7 %
All Questions for Topic 12.2 – Rutherford scattering and nuclear radius , Nuclear energy levels , The neutrino , The law of radioactive decay and the decay constant
Question
What was a reason to postulate the existence of neutrinos?
Nuclear energy levels had a continuous spectrum.
The photon emission spectrum only contained specific wavelengths.
Some particles were indistinguishable from their antiparticle.
The energy of emitted beta particles had a continuous spectrum.
▶️Answer/Explanation
Ans: D
Wolfgang Pauli hypothesised the existence of a third particle in the products of a beta decay in 1933. Since the energy of the electron in beta decay has a range of possible values, it means that a third very light particle must also be produced so that it carries the remainder of the available energy. Enrico Fermi coined the word neutrino for the ‘little neutral one.
Question
The graphs show the variation with time of the activity and the number of remaining nuclei for a sample of a radioactive nuclide.
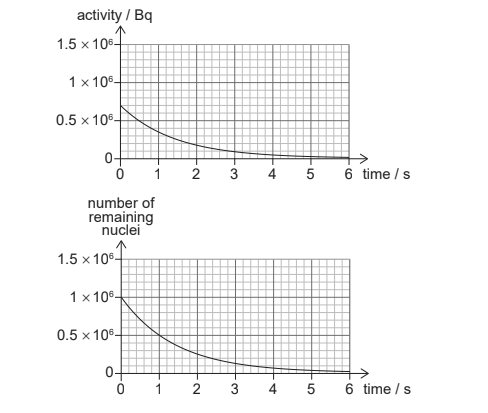
What is the decay constant of the nuclide?
A. 0.7 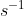
B. 1 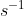
C.
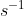
D. 1.5 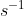
▶️Answer/Explanation
Ans: A
\(=N_0 \lambda e^{-\lambda \times 0} =N_0 \lambda\)
Hence
\(\lambda =\frac{\left [ R \right ]_0}{N_0}\)
\(=\frac{0.7\times 10^6}{1\times 10^6}\)
\(=0.7\)
Question
Two samples X and Y of different radioactive isotopes have the same initial activity. Sample X has twice the number of atoms as sample Y. The half-life of X is T. What is the half-life of Y?
A. 2T
B. T
C. \(\frac{T}{2}\)
D. \(\frac{T}{4}\)
▶️Answer/Explanation
Markscheme
C
Initial activity
\(\left [ R \right ]_0=N_0 \lambda e^{-\lambda t}\)
\(=N_0 \lambda e^{-\lambda \times 0} =N_0 \lambda\)
Hence
\(\lambda =\frac{\left [ R \right ]_0}{N_0}\)
Sample X and Y has same initial activity Also
\(N_{OX}=2N_{OY}\)
and
\(T_{1/2(X)}= T T_{1/2(Y)}= ?\)
\(N_{OX}\lambda_X=N_{OY}\lambda_Y\)
\(\lambda =\frac{0.63}{T_{1/2}}\)
hence
\(\frac{N_{OX}}{T_{1/2(X)}} =\frac{N_{OY}}{T_{1/2(Y)}}\)
or
\(T_{1/2(Y)} =\frac{N_{OY}}{N_{OX}}\times T_{1/2(X)}\)
\(=\frac{T_{1/2(X)}}{2}=\frac{T}{2}\)
Question
An electron of initial energy E tunnels through a potential barrier. What is the energy of the electron after tunnelling?
A. greater than E
B. E
C. less than E
D. zero
▶️Answer/Explanation
Markscheme
B
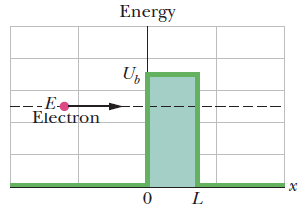
Energy of electron remain same.
Question
Two radioactive nuclides, X and Y, have half-lives of 50 s and 100 s respectively. At time t = 0 samples of X and Y contain the same number of nuclei.
What is \(\frac{{{\text{number of nuclei of X undecayed}}}}{{{\text{number of nuclei of Y undecayed}}}}\) when t = 200 s?
A. 4
B. 2
C. \(\frac{1}{2}\)
D. \(\frac{1}{4}\)
▶️Answer/Explanation
Markscheme
D
\(N_t=\frac{N_o}{2^n}\) where n is number of half life
For nuclides X \(n_x=\frac{200}{50}=4\)
for nuclides Y \(n_y=\frac{200}{100}=2\)
Also given that \(N_{0X} =N_{0X}\)
Hence
\(\frac{ N_{tX}}{ N_{tY}}=\frac{\frac{N_o}{2^{n_x}}}{\frac{N_o}{2^{n_y}}}\)
\(=\frac{2^2}{2^4}=\frac{1}{4}\)
Question
Alpha particles with energy E are directed at nuclei with atomic number Z. Small deviations from the predictions of the Rutherford scattering model are observed.
Which change in E and which change in Z is most likely to result in greater deviations from the Rutherford scattering model?

▶️Answer/Explanation
Markscheme
B
The derivation of the Rutherford formula is based on a number of assumptions. The most important is that the only force in play during the scattering process is the electric force. As the energy of the alpha particles increases, the alpha particles can get closer to the nucleus. When the distance of closest approach gets to be about 10−15 m or less, deviations from the Rutherford formula are observed . This is due to the fact that the alpha particles are so close to the nucleus that the strong nuclear force begins to act on the alpha particles. Hence nuclear force is felt with high energy and smaller Z .
Question
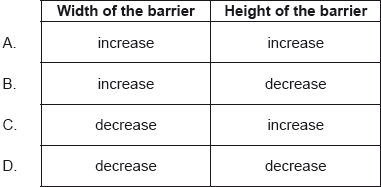
A particle of fixed energy is close to a potential barrier.
Which changes to the width of the barrier and to the height of the barrier will always make the tunnelling probability greater?
▶️Answer/Explanation
Markscheme
D

An energy diagram containing two plots for the situation of Fig. above:
- The electron’s mechanical energy E is plotted when the electron is at any coordinate x < 0.
- The electron’s electric potential energy U is plotted as a function of the electron’s position x, assuming that the electron can reach any value of x.
- The nonzero part of the plot (the potential barrier) has height Ub and thickness L.
For a particle with mass m and a barrier of thickness L, the transmission coefficient is
\(T\approx e^{-2bL}\)
where
\(b=\sqrt{\frac{8\pi ^2 m(U_b-E)}{h^2}}\)
hence for Smaller \(L\) and \(U_b-E\) , \(T\) is greater
Question
A radioactive element has decay constant \(\lambda \) (expressed in s–1). The number of nuclei of this element at t = 0 is N. What is the expected number of nuclei that will have decayed after 1 s?
A. \(N\left( {1 – {e^{ – \lambda }}} \right)\)
B. \(\frac{N}{\lambda }\)
C. \(N{e^{ – \lambda }}\)
D. \(\lambda N\)
▶️Answer/Explanation
Markscheme
A
Number of nuclei after time \(t\) is given by
\(N_t= N_0 e^{-\lambda t}\)
Now after 1 sec
\(N_1=N e^{-\lambda}\)
hence Number of Nuclei declayed
\(= N – N_1\)
\(=N-N e^{-\lambda}\)
\(=N(1-e^{-\lambda})\)
Question
What was a reason to postulate the existence of neutrinos?
Nuclear energy levels had a continuous spectrum.
The photon emission spectrum only contained specific wavelengths.
Some particles were indistinguishable from their antiparticle.
The energy of emitted beta particles had a continuous spectrum.
▶️Answer/Explanation
Ans: D
Wolfgang Pauli hypothesised the existence of a third particle in the products of a beta decay in 1933. Since the energy of the electron in beta decay has a range of possible values, it means that a third very light particle must also be produced so that it carries the remainder of the available energy. Enrico Fermi coined the word neutrino for the ‘little neutral one.