IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.3 – Work , Energy and Power
Topic 2 Weightage : 13 %
All Questions for Topic 2.3 – Kinetic energy , Gravitational potential energy , Elastic potential energy ,Work done as energy transfer , Power as rate of energy transfer , Principle of conservation of energy , Efficiency
This question is in two parts. Part 1 is about the motion of a ship. Part 2 is about melting ice.
Part 1 Motion of a ship
Some cargo ships use kites working together with the ship’s engines to move the vessel.
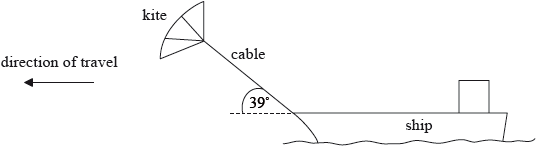
The tension in the cable that connects the kite to the ship is 250 kN. The kite is pulling the ship at an angle of 39° to the horizontal. The ship travels at a steady speed of \({\text{8.5 m}}\,{{\text{s}}^{ – 1}}\) when the ship’s engines operate with a power output of 2.7 MW.
The ship’s engines are switched off and the ship comes to rest from a speed of \({\text{7 m}}\,{{\text{s}}^{ – 1}}\) in a time of 650 s.
Part 2 Melting ice
A container of negligible mass, isolated from its surroundings, contains 0.150 kg of ice at a temperature of –18.7 °C. An electric heater supplies energy at a rate of 125 W.
a. Outline the meaning of work. [2]
\[F = k{v^2}\]
where \(k\) is a constant.
Show that, if the power output of the engines remains at 2.7 MW, the speed of the ship will decrease to about \({\text{7 m}}\,{{\text{s}}^{ – 1}}\). Assume that \(k\) is independent of whether the kite is in use or not. [3]
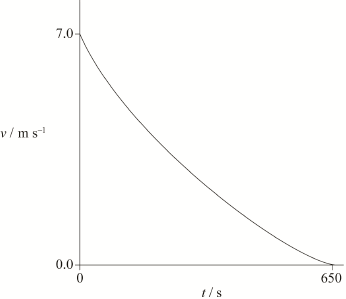
 [2]
[2]
Specific heat capacity of water \( = 4200{\text{ J}}\,{\text{k}}{{\text{g}}^{ – 1}}{{\text{K}}^{ – 1}}\)
Specific latent heat of fusion of ice \( = 3.30 \times {10^5}{\text{ J}}\,{\text{k}}{{\text{g}}^{ – 1}}\)
Determine the final temperature of the water when the heater supplies energy for a further 600 s. [3]
▶️Answer/Explanation
Markscheme
a. \({\text{work done}} = {\text{force}} \times {\text{distance moved}}\);
(distance moved) in direction of force;
or
energy transferred;
from one location to another;
or
\({\text{work done}} = Fs\cos \theta \);
with each symbol defined;
\({\text{horizontal force}} = 250\,000 \times \cos 39^\circ {\text{ }}( = 1.94 \times {10^5}{\text{ N}})\);
\({\text{work done}} = 1.9 \times {10^8}{\text{ J}}\);
\({\text{power provided by kite}} = (1.94 \times {10^5} \times 8.5 = ){\text{ }}1.7 \times {10^6}{\text{ W}}\);
\({\text{total power}} = (2.7 + 1.7) \times {10^6}{\text{ W }}( = 4.4 \times {10^6}{\text{ W}})\);
\({\text{fraction provided by kite}} = \frac{{1.7}}{{2.7 + 1.7}}\);
38% or 0.38; (must see answer to 2+ sig figs as answer is given)
Allow answers in the range of 37 to 39% due to early rounding.
or
Award [3 max] for a reverse argument such as:
if 2.7 MW is 60%;
then kite power is \(\frac{2}{3} \times 2.7{\text{ MW}} = 1.8{\text{ MW}}\);
shows that kite power is actually 1.7 MW; (QED)
\(P = (k{v^2}) \times v = k{v^3}\);
\(\frac{{{v_1}}}{{{v_2}}} = \left( {\sqrt[3]{{\left( {\frac{{{P_1}}}{{{P_2}}}} \right)}} = } \right){\text{ }}\sqrt[3]{{\left( {\frac{{7.7}}{{4.4}}} \right)}}\);
\({\text{final speed of ship}} = 7.2{\text{ m}}\,{{\text{s}}^{ – 1}}\); (at least 2 sig figs required).
Approximate answer given, marks are for working only.
an answer in the range of 2200 to 2400 m;
starts at \(7.0/7.2{\text{ m}}\,{{\text{s}}^{ – 1}}\); (allow ECF from (d)(i))
correct shape;
in ice, molecules vibrate about a fixed point;
as their total energy increases, the molecules (partly) overcome the attractive force between them;
in liquid water the molecules are able to migrate/change position;
\((Q = ){\text{ }}45.0 \times 125{\text{ }}( = 5625{\text{ J}})\);
\(c = \left( {\frac{Q}{{m\Delta \theta }} = } \right){\text{ }}2.01 \times {10^3}{\text{ J}}\,{\text{k}}{{\text{g}}^{ – 1}}{{\text{K}}^{ – 1}}\);
\({\text{energy available}} = 125 \times 600{\text{ }}( = 75000{\text{ J}})\);
\({\text{energy available to warm the water}} = 75000 – [0.15 \times 3.3 \times {10^5}]{\text{ }}( = 25500{\text{ J}})\);
\({\text{temperature}} = \left( {\frac{{25500}}{{0.15 \times 4200}} = } \right){\rm{ 40.5 ^\circ C}}\);
ice/water spends more time below 18 °C;
so net energy transfer is in to the system;
so final water temperature is higher;
or
ice/water spends less time below 18 °C;
so net energy transfer is out of the system;
so final water temperature is lower;
Examiners report
Many good answers, although those that did not get the correct answers presented their working in such a way that part marks (ECF) were not able to be given.
The significance of the temperature of the surroundings was ignored by nearly all candidates, but most were able to obtain 2 marks for suggesting that thermal energy would be lost to the surroundings causing a lower final temperature.
This question is in two parts. Part 1 is about the motion of a car. Part 2 is about electricity.
Part 1 Motion of a car
A car is travelling along the straight horizontal road at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\). The power output required at the wheels is 0.13 MW.
A driver moves the car in a horizontal circular path of radius 200 m. Each of the four tyres will not grip the road if the frictional force between a tyre and the road becomes less than 1500 N.
Part 2 Electricity
A lemon can be used to make an electric cell by pushing a copper rod and a zinc rod into the lemon.
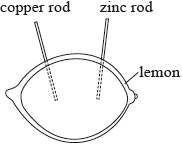
A student constructs a lemon cell and connects it in an electrical circuit with a variable resistor. The student measures the potential difference V across the lemon and the current I in the lemon.
a. A car accelerates uniformly along a straight horizontal road from an initial speed of \({\text{12 m}}\,{{\text{s}}^{ – 1}}\) to a final speed of \({\text{28 m}}\,{{\text{s}}^{ – 1}}\) in a distance of 250 m. The mass of the car is 1200 kg. Determine the rate at which the engine is supplying kinetic energy to the car as it accelerates. [4]
(i) Calculate the total resistive force acting on the car when it is travelling at a constant speed of \({\text{56 m}}\,{{\text{s}}^{ – 1}}\).
(ii) The mass of the car is 1200 kg. The resistive force \(F\) is related to the speed \(v\) by \(F \propto {v^2}\). Using your answer to (b)(i), determine the maximum theoretical acceleration of the car at a speed of \({\text{28 m}}\,{{\text{s}}^{ – 1}}\). [5]
(i) Calculate the maximum speed of the car at which it can continue to move in the circular path. Assume that the radius of the path is the same for each tyre.
(ii) While the car is travelling around the circle, the people in the car have the sensation that they are being thrown outwards. Outline how Newton’s first law of motion accounts for this sensation. [6]
(i) Draw a circuit diagram of the experimental arrangement that will enable the student to collect the data for the graph.
(ii) Show that the potential difference \(V\) across the lemon is given by
\[V = E – Ir\]
where \(E\) is the emf of the lemon cell and \(r\) is the internal resistance of the lemon cell.
(iii) The graph shows how \(V\) varies with \(I\).
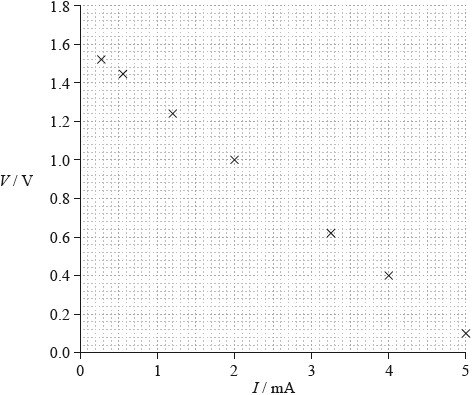
Using the graph, estimate the emf of the lemon cell.
(iv) Determine the internal resistance of the lemon cell.
(v) The lemon cell is used to supply energy to a digital clock that requires a current of \({\text{6.0 }}\mu {\text{A}}\). The clock runs for 16 hours. Calculate the charge that flows through the clock in this time.
▶️Answer/Explanation
Markscheme
a. use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
change in kinetic energy \( = \frac{1}{2} \times 1200 \times \left[ {{{28}^2} – {{12}^2}} \right]{\text{ }}( = 384{\text{ kJ)}}\);
rate of change in kinetic energy \( = \frac{{384000}}{{12.5}}\); } (allow ECF of 162 from (28 – 12)2 for this mark)
31 (kW);
or
use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
use of a kinematic equation to determine acceleration \(( = {\text{1.28 m}}\,{{\text{s}}^{ – 2}}{\text{)}}\);
work done \( = \frac{{F \times s}}{{{\text{time}}}} = \frac{{1536 \times 250}}{{12.5}}\);
31 (kW);
(i) \({\text{force}} = \frac{{{\text{power}}}}{{{\text{speed}}}}\);
2300 or 2.3k (N);
Award [2] for a bald correct answer.
(ii) resistive force \( = \frac{{2300}}{4}\)\(\,\,\,\)or\(\,\,\,\)\(\frac{{2321}}{4}{\text{ }}( = 575)\); (allow ECF)
so accelerating force = \((2300 – 580 = ){\text{ }}1725{\text{ (N)}}\)\(\,\,\,\)or\(\,\,\,\)1741 (N);
\(a = \frac{{1725}}{{1200}} = 1.44{\text{ (m}}{{\text{s}}^{ – 2}}{\text{)}}\)\(\,\,\,\)or\(\,\,\,\)\(a = \frac{{1741}}{{1200}} = 1.45{\text{ (m}}\,{{\text{s}}^{ – 2}}{\text{)}}\);
Award [2 max] for an answer of 0.49 (m\(\,\)s–2) (omits 2300 N).
(i) centripetal force must be \( < {\text{6000 (N)}}\); (allow force = 6000 N)
\({v^2} = F \times \frac{r}{m}\);
\({\text{31.6 (m}}\,{{\text{s}}^{ – 1}}{\text{)}}\);
Allow [3] for a bald correct answer.
Allow [2 max] if 4\( \times \) is omitted, giving 15.8 (m\(\,\)s–1).
(ii) statement of Newton’s first law;
(hence) without car wall/restraint/friction at seat, the people in the car would move in a straight line/at a tangent to circle;
(hence) seat/seat belt/door exerts centripetal force;
(in frame of reference of the people) straight ahead movement is interpreted as “outwards”;
(i) voltmeter in parallel with cell; (allow ammeter within voltmeter leads)
ammeter in series with variable resistor; } (must draw as variable arrangement or as potential divider)
Allow cell symbol for lemon/cell/box labelled “lemon cell”.
Award [1 max] if additional cell appears in the circuit.
(ii) \(E = I(R + r)\) and \(V = IR\) used; (must state both explicitly)
re-arrangement correct ie \(E = V + Ir\); } (accept any other correct re-arrangement eg. involving energy conversion)
(iii) line correctly extrapolated to y-axis; (judge by eye)
1.6 or 1.60 (V); (allow ECF from incorrect extrapolation)
(iv) correct read-offs from large triangle greater than half line length;
gradient determined;
290 to 310 \({\text{(}}\Omega {\text{)}}\);
Award [2 max] for the use of one point on line and equation.
(v) 0.35 (C);
Examiners report
a. There were at least two routes to tackle this problem. Some solutions were so confused that it was difficult to decide which method had been used. Common errors included: forgetting that the initial speed was \({\text{12 m}}\,{{\text{s}}^{ – 1}}\) not zero, power of ten errors, and simple mistakes in the use of the kinematic equations, or failure to evaluate work done = force \( \times \) distance correctly. However, many candidates scored partial credit. Scores of two or three out of the maximum four were common showing that many are persevering to get as far as they can.
(i) Many correct solutions were seen. Candidates are clearly comfortable with the use of the equation force = power/speed.
(ii) The method to be used here was obvious to many. What was missing was a clear appreciation of what was happening in terms of resistive force in the system. Many scored two out of three because they indicated a sensible method but did not use the correct value for the force. Scoring two marks does require that the explanation of the method is at least competent. Those candidates who give limited explanations of their method leading to a wrong answer will generally accumulate little credit. A suggestion (never seen in answers) is that candidates should have begun from a free-body force diagram which would have revealed the relationship of all the forces.
(i) The major problem here was that most candidates did not recognise that 1500 N of force acting at each of four wheels will imply a total force of 6 kN. Again, partial credit was available only if it was clear what the candidate was doing and what the error was.
(ii) Statements of Newton’s first law were surprisingly poor. As in previous examinations, few candidates appear to have learnt this essential rule by heart and they produce a garbled and incomplete version under examination pressure. The first law was then only loosely connected to the particular context of the question. Candidates have apparently not learnt to relate the physics they learn to everyday contexts.
(i) Circuit diagrams continue to be a particular issue for many candidates. Neat, well-drawn diagrams are rarely seen. Some diagrams had two cells, the lemon cell and another. Variable resistors were sometimes absent (or were drawn as fixed). Potential dividers were often attempted usually unsuccessfully. Generally candidates gained an average one mark for what should have been a familiar task.
(ii) Those who quoted the data booklet equation and the definition of resistance were generally able to show the final expression. Some however could not convince the examiners that they knew what they were doing.
(iii) Candidates were expected to understand the physical point that the emf can be determined when the current in the cell is zero. For many, an extrapolation of the obvious straight line to the emf axis and a correct read-off gave an easy couple of marks. Some however did not understand the physics of the circuit and gave poorly described solutions.
(iv) The internal resistance was best obtained from a large triangle drawn on the graph. Many however gained two of the three marks because they engendered power of ten errors or because they used only one point, or because their triangle was too small.
(v) Only a minority were able to use the data to calculate the charge transferred correctly.
Impulse and momentum
The diagram shows an arrangement used to test golf club heads.
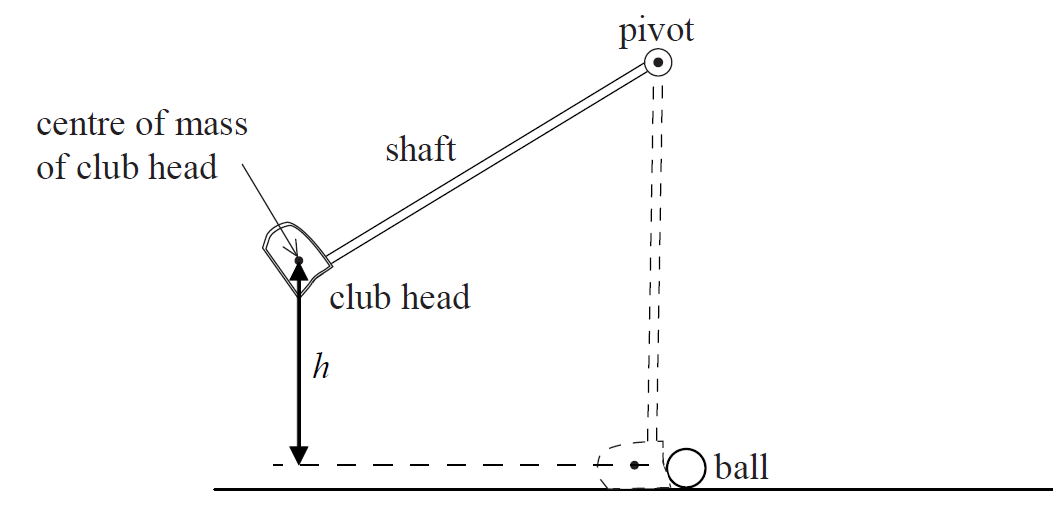
The shaft of a club is pivoted and the centre of mass of the club head is raised by a height h before being released. On reaching the vertical position the club head strikes the ball.
a. (i) Describe the energy changes that take place in the club head from the instant the club is released until the club head and the ball separate.
(ii) Calculate the maximum speed of the club head achievable when h = 0.85 m. [4]
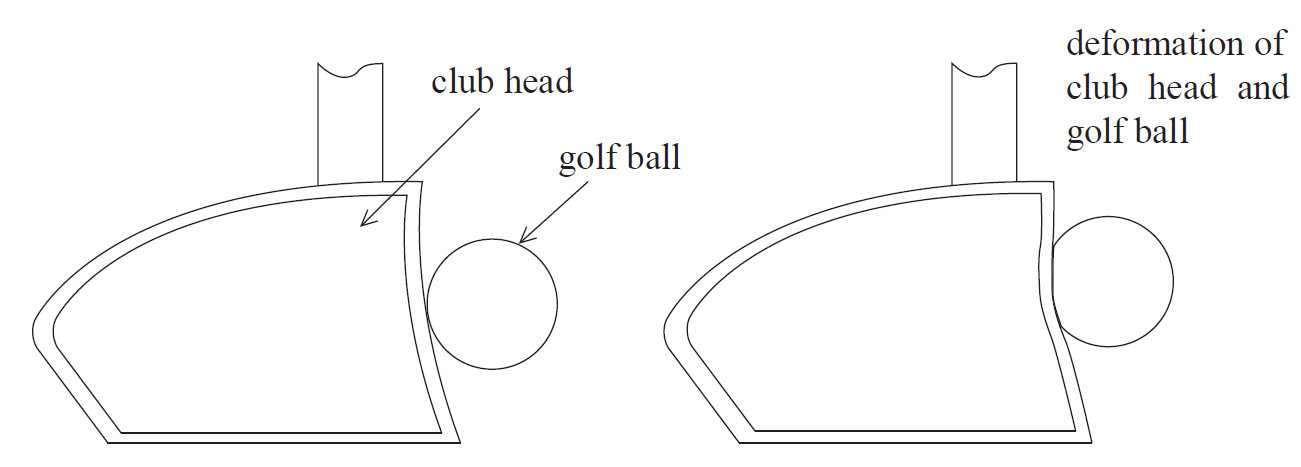
Explain how increasing the deformation of the club head may be expected to increase the speed at which the ball leaves the club. [2]
In a different experimental arrangement, the club head is in contact with the ball for a time of 220 μs. The club head has mass 0.17 kg and the ball has mass 0.045 kg. At the moment of contact the ball is at rest and the club head is moving with a speed of 38 ms–1. The ball moves off with an initial speed of 63 ms–1.
(i) Calculate the average force acting on the ball while the club head is in contact with the ball.
(ii) State the average force acting on the club head while it is in contact with the ball.
(iii) Calculate the speed of the club head at the instant that it loses contact with the ball. [5]
▶️Answer/Explanation
Markscheme
a. (i) (gravitational) potential energy (of club head) goes to kinetic energy (of club head);
some kinetic energy of club head goes to internal energy of club head/kinetic energy of ball;
(ii) equating mgh to \(\frac{1}{2}\)mv2 ;
v=4.1(ms-1);
Award [0] for answers using equation of motion – not uniform acceleration.
deformation prolongs the contact time;
increased impulse => bigger change of momentum/velocity;
or
(club head) stores (elastic) potential energy on compression;
this energy is passed to the ball;
(i) any value of \(\frac{{{\rm{mass}} \times {\rm{velocity}}}}{{{\rm{time}}}}\);
1.3 x 104 (N);
(ii)-1.3 x 10-4 (N);
Accept statement that force is in the opposite direction to (c)(i).
Allow the negative of any value given in (c)(i).
(iii) clear use of conservation of momentum / impulse = change of momentum;
21(ms-1 );
or
a=\(\left( {\frac{{\rm{F}}}{{\rm{m}}} = \frac{{ – 13000}}{{0.17}} = } \right)\left( – \right)76500\left( {{\rm{m}}{{\rm{s}}^{ – 1}}} \right)\);
v=(u+at=38-76500 x 0.00022=) 21(ms-1);
Award [2] for a bald correct answer.
Examiners report
a. (i) Nearly all candidates gained a mark for recognising the change from kinetic to potential energy in this part. Fewer recognised that the club head would not transfer all of its energy to the ball and therefore retained a significant amount of energy.
(ii) This part was well done by many.
A minority of candidates became bogged down by the deformation of the ball and club head idea and ventured into elastic potential energy ideas. This had a successful outcome in many cases when there was discussion of the compression providing further kinetic energy to the ball on recovering its shape. The most straightforward solution was to use to principle of impulse being equal to the change in momentum (as shown in the question heading) and simply to recognise that an increased contact time would be expected to give a greater change of momentum for a constant force.
(i) This was well done with the only real problem being deciding which was the speed change of the ball.
(ii) Less candidates than anticipated recognised that the force on the club head was equal and opposite to that acting on the ball (applying Newton’s third law of motion).
(iii) Most made a good attempt at calculating the speed of the club head.