IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.4 – Momentum and impluse
Topic 2 Weightage : 13 %
All Questions for Topic 2.4 – Newton’s second law expressed in terms of rate of change of momentum ,Impulse and force–time graphs , Conservation of linear momentum , Elastic collisions, inelastic collisions and explosions
This question is in two parts. Part 1 is about momentum. Part 2 is about electric point charges.
Part 1 Momentum
Part 2 Electric point charges
a. State the law of conservation of linear momentum. [2]
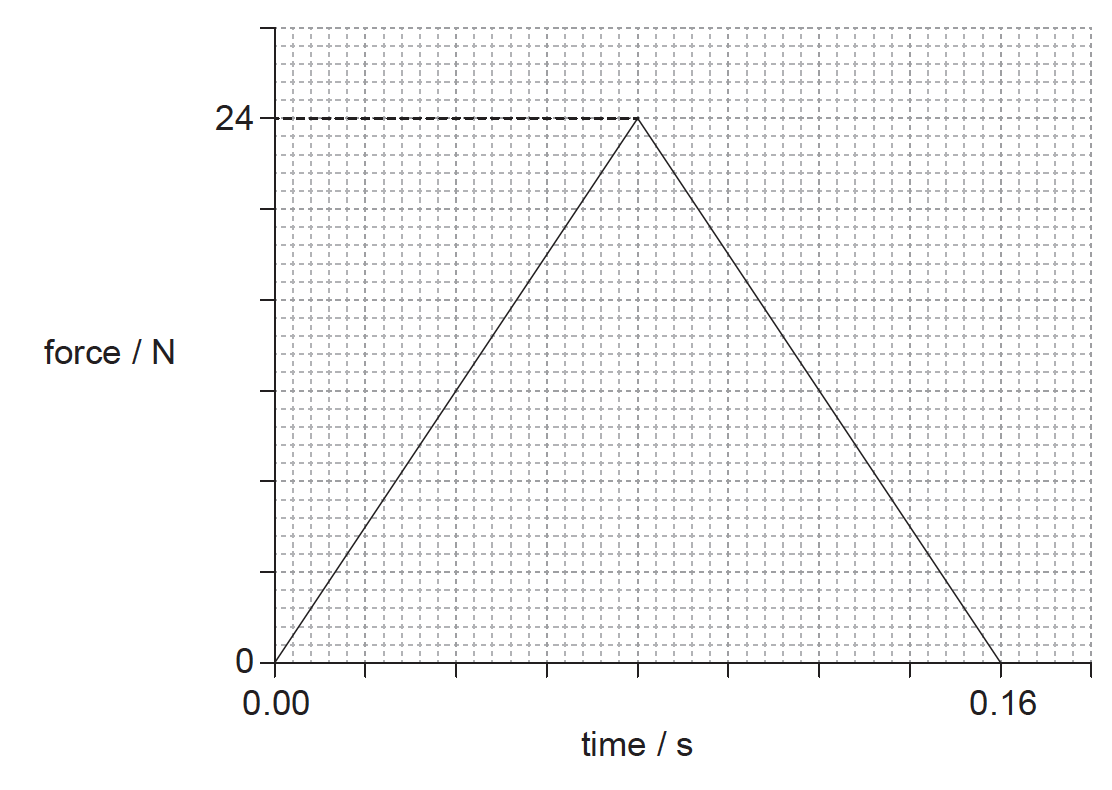
The graph shows the variation with time of the force acting on the car due to the wall during the collision.
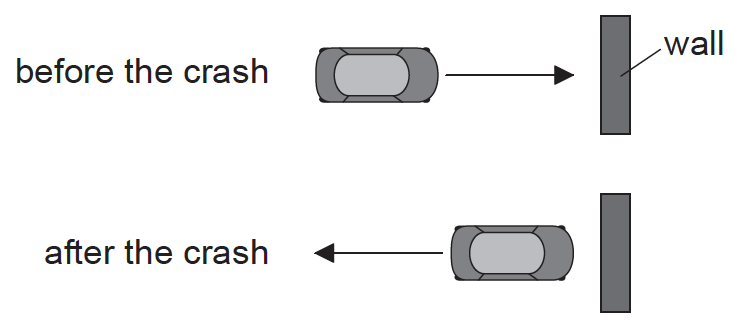
 The kinetic energy of the car is unchanged after the collision. The mass of the car is 0.80 kg.
The kinetic energy of the car is unchanged after the collision. The mass of the car is 0.80 kg.
(i) Determine the initial momentum of the car.
(ii) Estimate the average acceleration of the car before it rebounds.
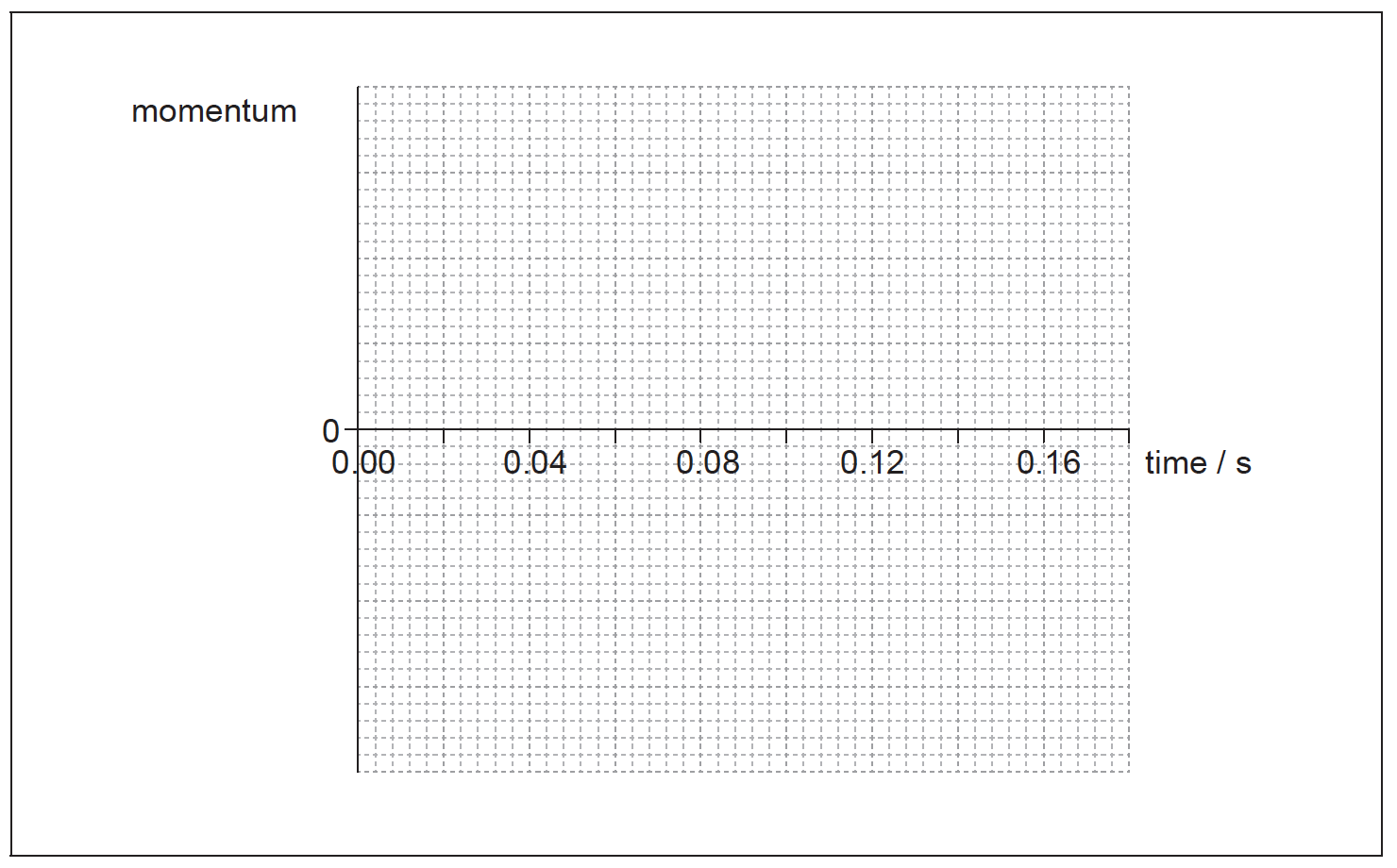
(iii) On the axes, draw a graph to show how the momentum of the car varies during the impact. You are not required to give values on the y-axis.
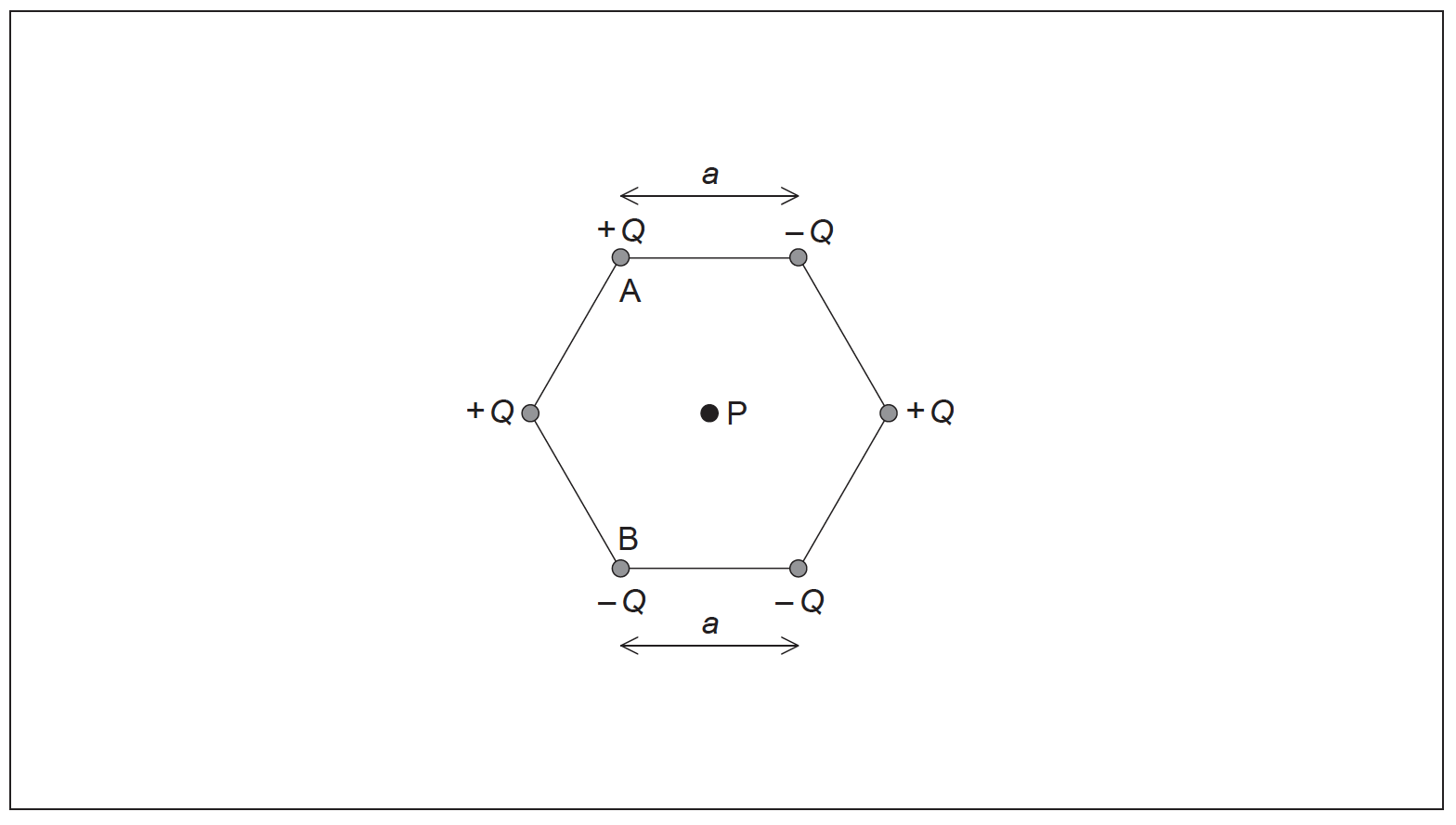
P is at the centre of the hexagon.
(i) Show, using Coulomb’s law, that the magnitude of the electric field strength at point P due to one of the point charges is
\[\frac{{kQ}}{{{a^2}}}\]
(ii) On the diagram, draw arrows to represent the direction of the field at P due to point charge A (label this direction A) and point charge B (label this direction B).
(iii) The magnitude of Q is 3.2 μC and length a is 0.15 m. Determine the magnitude and the direction of the electric field strength at point P due to all six charges. [8]
▶️Answer/Explanation
Markscheme
a.total momentum does not change/is constant; } (do not allow “momentum is conserved”)
provided external force is zero / no external forces / isolated system;
(i) clear attempt to calculate area under graph;
initial momentum is half change in momentum;
\(\left( {\frac{1}{2} \times \frac{1}{2} \times 24 \times 0.16} \right) = 0.96\left( {{\rm{kgm}}{{\rm{s}}^{ – 1}}} \right)\)
Award [2 max] for calculation of total change (1.92kg ms–1)
(ii) initial speed \( = \left( {\frac{{0.96}}{{0.8}} = } \right)1.2{\rm{m}}{{\rm{s}}^{ – 1}}\);
\(a = \frac{{1.2 – \left( { – 1.2} \right)}}{{0.16}}\) or \(a = \frac{{ – 1.2 – 1.2}}{{0.16}}\);
–15(ms–2); (must see negative sign or a comment that this is a deceleration)
or
average force =12 N;
uses F=0.8×a ;
–15(ms–2); (must see negative sign or a comment that this is a deceleration)
Award [3] for a bald correct answer.
Other solution methods involving different kinematic equations are possible.
(iii) goes through t=0.08s and from negative momentum to positive / positive momentum to negative;
constant sign of gradient throughout;
curve as shown;
Award marks for diagram as shown.
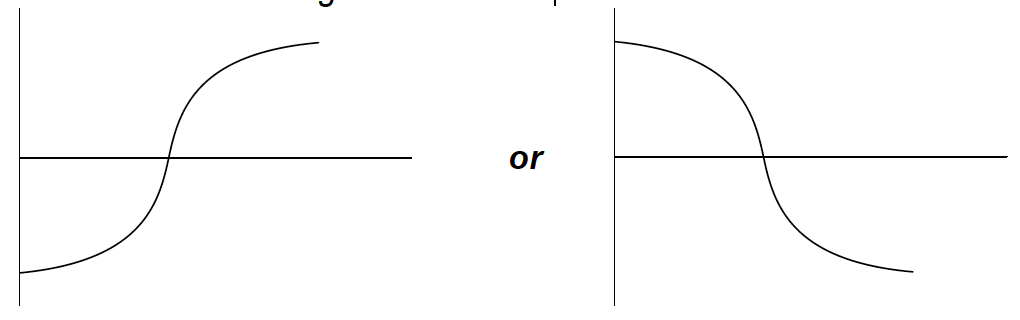
impulse is the same/similar in both cases / momentum change is same;
impulse is force × time / force is rate of change of momentum;
time to come to rest is longer for car B;
force experienced by car B is less (so less likely to be damaged);
electric force per unit charge;
acting on a small/point positive (test) charge;
(i) states Coulomb’s law as \(\frac{{kQq}}{{{r^2}}}\) or \(\frac{F}{q} = \frac{{kQ}}{{{r^2}}}\)
states explicitly q=1;
states r=a;
(ii) 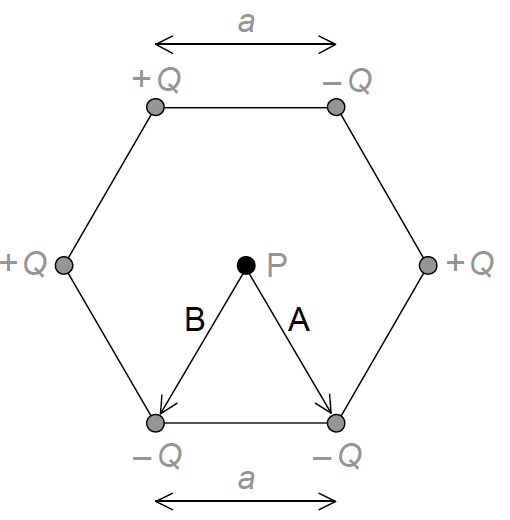
arrow labelled A pointing to lower right charge;
arrow labelled B point to lower left charge;
Arrows can be anywhere on diagram.
(iii) overall force is due to +Q top left and -Q bottom right / top right and bottom left and centre charges all cancel; } (can be seen on diagram)
force is therefore \(\frac{{2kQ}}{{{a^2}}}\);
2.6×106 (N C-1) ;
towards bottom right charge; (allow clear arrow on diagram showing direction)
This question is about the use of energy resources.
Electrical energy is obtained from tidal energy at La Rance in France.
Water flows into a river basin from the sea for six hours and then flows from the basin back to the sea for another six hours. The water flows through turbines and generates energy during both flows.
The following data are available.
Area of river basin \( = 22{\text{ k}}{{\text{m}}^{\text{2}}}\)
Change in water level of basin over six hours \( = 6.0{\text{ m}}\)
Density of water \( = 1000{\text{ kg}}\,{{\text{m}}^{ – 3}}\)
Nuclear reactors are used to generate energy. In a particular nuclear reactor, neutrons collide elastically with carbon-12 nuclei \(\left( {_{\;{\text{6}}}^{{\text{12}}}{\text{C}}} \right)\) that act as the moderator of the reactor. A neutron with an initial speed of \(9.8 \times {10^6}{\text{ m}}\,{{\text{s}}^{ – 1}}\) collides head-on with a stationary carbon-12 nucleus. Immediately after the collision the carbon-12 nucleus has a speed of \(1.5 \times {10^6}{\text{ m}}\,{{\text{s}}^{ – 1}}\).
a. State the difference between renewable and non-renewable energy sources. [1]
(ii) Show that the average power that the water can supply over the six hour period is about 0.2 GW.
(iii) La Rance tidal power station has an energy output of \(5.4 \times {10^8}{\text{ kW}}\,{\text{h}}\) per year. Calculate the overall efficiency of the power station. Assume that the water can supply 0.2 GW at all times.
Energy resources such as La Rance tidal power station could replace the use of
fossil fuels. This may result in an increase in the average albedo of Earth.
(iv) State two reasons why the albedo of Earth must be given as an average value. [10]
(i) State the principle of conservation of momentum.
(ii) Show that the speed of the neutron immediately after the collision is about \(8.0 \times {10^6}{\text{ m}}\,{{\text{s}}^{ – 1}}\).
(iii) Show that the fractional change in energy of the neutron as a result of the collision
is about 0.3.
(iv) Estimate the minimum number of collisions required for the neutron to reduce its initial energy by a factor of \({10^6}\).
(v) Outline why the reduction in energy is necessary for this type of reactor to function.
▶️Answer/Explanation
Markscheme
a. only non-renewable is depleted/cannot re-generate whereas renewable can / consumption rate of non-renewables is greater than formation rate and consumption rate of renewables is less than formation rate;
Do not allow “cannot be used again”.
(i) volume released = \((22 \times {10^6} \times 6 = ){\text{ }}1.32 \times {10^8}{\text{ (}}{{\text{m}}^3}{\text{)}}\);
volume per second \(\frac{{1.32 \times {{10}^8}}}{{6 \times 3600}}{\text{ }}( = 6111{\text{ }}{{\text{m}}^3})\);
(ii) use of average depth for calculation (3 m);
gpe lost \(6100 \times 1000 \times 9.81 \times 3\);
0.18 (GW);
Accept g = 10 m\(\,\)s–2.
Award [1 max] if 6 m is used and an “average” is used at end of solution without mention of average depth.
(iii) converts/states output with units; } (allow values quoted from question without unit)
converts/states input with units; } (allow values quoted from question without unit)
calculates efficiency from \(\frac{{{\text{output}}}}{{{\text{input}}}}\) as 0.31;
Award [3] for bald correct answer.
eg:
power output \(\frac{{5.4 \times {{10}^8}}}{{365 \times 24 \times 3600}}{\text{ }}\left( { = 17{\text{ kW}}\,{\text{h}}\,{{\text{s}}^{ – 1}}} \right)\);
\( = 17 \times 3600000 = 6.16 \times {10^7}{\text{ (W)}}\);
efficiency = \(\left( {\frac{{6.16 \times {{10}^7}}}{{2.0 \times {{10}^8}}} = } \right){\text{ }}31\% \)\(\,\,\,\)or\(\,\,\,\)0.31;
or
0.2 GW is \(1.752 \times {10^9}{\text{ (kW}}\,{\text{h}}\,{\text{yea}}{{\text{r}}^{ – 1}}{\text{)}}\);
\(\frac{{5.4 \times {{10}^8}}}{{1.752 \times {{10}^9}}}\);
efficiency \( = 0.31\);
(iv) cloud cover / weather conditions;
latitude;
time of year / season;
nature/colour of surface;
(i) (total) momentum unchanged before and after collision / momentum of a system is constant; } (allow symbols if explained)
no external forces / isolated system / closed system;
Do not accept “conserved”.
(ii) final momentum of neutron \( = {\text{neutron mass}} \times 9.8 \times {10^6} – 1{\text{u}} \times 12 \times 1.5 \times {10^6}\); } (allow any appropriate and consistent mass unit)
final speed of neutron \( = 8.0\)\(\,\,\,\)or\(\,\,\,\)\(8.2 \times {10^6}{\text{ (m}}\,{{\text{s}}^{ – 1}}{\text{)}}\);
\(\left( { \approx {\text{8.0}} \times {\text{1}}{{\text{0}}^6}{\text{ (m}}\,{{\text{s}}^{ – 1}}{\text{)}}} \right)\)
Allow use of 1 u for both masses giving an answer of 8.2 \( \times \) 106 (m\(\,\)s–1).
(iii) initial energy of neutron \( = 8.04 \times {10^{ – 14}}{\text{ (J)}}\) and final energy of neutron \( = 5.36 \times {10^{ – 14}}{\text{ (J)}}\); } (both needed)
fractional change in energy \( = \left( {\frac{{(8.04 – 5.36)}}{{8.04}} = } \right){\text{ }}0.33\);
or
fractional change \( = \left( {\frac{{\frac{1}{2}mv_{\text{i}}^2 – \frac{1}{2}mu_{\text{f}}^2}}{{\frac{1}{2}mv_{\text{i}}^2}}} \right)\); }(allow any algebra that shows a subtraction of initial term from final term divided by initial value)
\(\left( { = \frac{{{{(9.8 \times {{10}^6})}^2} – {{(8.0 \times {{10}^6})}^2}}}{{{{(9.8 \times {{10}^6})}^2}}}} \right)\) (allow omission of 106)
\( = 0.33\); (allow 0.30 if 8.2 used)
Do not allow ECF if there is no subtraction of energies in first marking point.
(iv) \({(0.33)^n} = {10^{ – 6}}\);
\(n = 13\); (allow n = 12 if 0.3 is used)
(v) neutrons produced in fission have large energies;
greatest probability of (further) fission/absorption (when incident neutrons have thermal energy or low energy);
Do not accept “reaction” for “fission reaction”.
Part 2 Momentum
b. State the law of conservation of momentum. [2]
The following data are available.
Mass of Jane = 52 kg
Mass of Joe = 74 kg
Mass of ball = 1.3 kg
Use the data to calculate the
(i) speed v of Jane relative to the ground immediately after she throws the ball.
(ii) speed V of Joe relative to the ground immediately after he catches the ball. [4]
▶️Answer/Explanation
Markscheme
b if the net external force acting on a system is zero;
the momentum of the system remains constant/unchanged/the same;
or
for a closed system;
the momentum remains constant/unchanged/the same;
Award [1] for “momentum before collision equals momentum after collision”.
Do not accept “momentum is conserved”.
no external forces act on this system / closed system;
increase/change in momentum of the gases is equal and opposite to the increase/change of momentum of the rocket;
v=0.20(ms-1);
Award [2] for a bald correct answer.
(ii) identifies new mass as 75.3(kg);
V=0.14(ms-1);