IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 3.1 – Thermal Concepts
Topic 3 Weightage : 6 %
All Questions for Topic 3.1 – Molecular theory of solids, liquids and gases , Temperature and absolute temperature , Internal energy , Specific heat capacity , Phase change , Specific latent heat
Question
A sample of vegetable oil, initially in the liquid state, is placed in a freezer that transfers thermal energy from the sample at a constant rate. The graph shows how temperature T of the sample varies with time t. 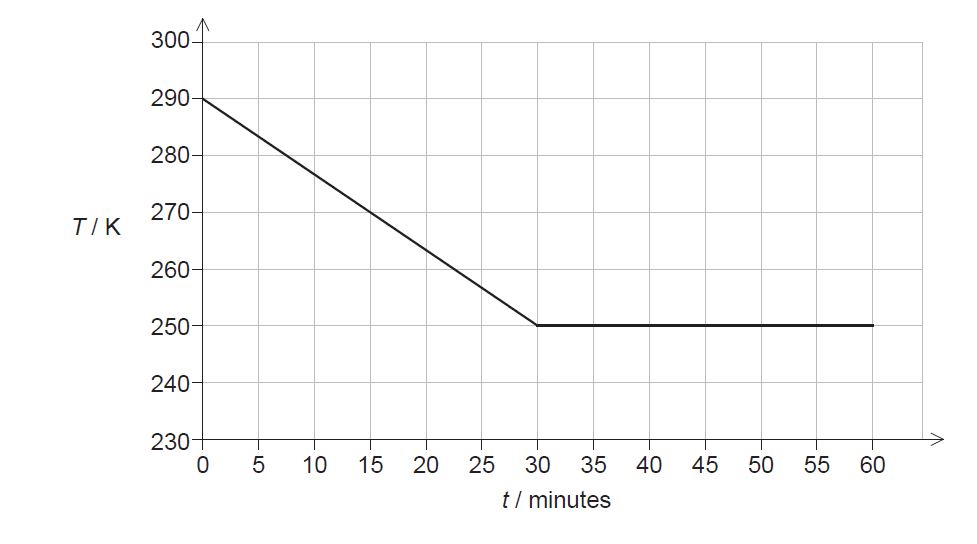
The following data are available.
Mass of the sample = 0.32 kg
Specific latent heat of fusion of the oil = 130 kJ kg–1
Rate of thermal energy transfer = 15 W
a. Calculate the thermal energy transferred from the sample during the first 30 minutes. [1]
b. Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.[2]
c. The sample begins to freeze during the thermal energy transfer. Explain, in terms of the molecular model of matter, why the temperature of the sample remains constant during freezing. [3]
d. Calculate the mass of the oil that remains unfrozen after 60 minutes.[2]
▶️Answer/Explanation
Ans:
a. «15x30x60» = 27000 «J»
b. 27 x 10 3 = 0.32 x c x (290 250) OR 2100 J kg -1 K -1 OR J kg -1 0 C -1
c.
«intermolecular» bonds are formed during freezing ✓
bond-forming process releases energy
OR
«intermolecular» PE decreases «and the difference is transferred as heat» ✓
«average random» KE of the molecules does not decrease/change ✓
temperature is related to «average» KE of the molecules «hence unchanged» ✓
d.
mass of frozen oil 27x 10 3/130 x 10 3 = 0.21 kg
unfrozen mass «= 0.32 −0.21» = 0.11«kg» ✓
Question
This question is about thermal properties of matter.
a
Explain, in terms of the energy of its molecules, why the temperature of a pure substance does not change during melting.[3]
Three ice cubes at a temperature of 0°C are dropped into a container of water at a temperature of 22°C. The mass of each ice cube is 25 g and the mass of the water is 330 g. The ice melts, so that the temperature of the water decreases. The thermal capacity of the container is negligible.
The following data are available.
Specific latent heat of fusion of ice \( = \) 3.3 \( \times \) 105J kg–1
Specific heat capacity of water \( = \) 4.2 \( \times \) 103 J kg–1 K–1
Calculate the final temperature of the water when all of the ice has melted. Assume that no thermal energy is exchanged between the water and the surroundings.[4]
▶️Answer/Explanation
Markscheme
a
energy supplied/bonds broken/heat absorbed;
increases potential energy;
no change in kinetic energy (so no change in temperature);
recognition that melted ice warms and water cools to common final temperature;
Question
This question is about internal energy.
(i) Mathilde raises the temperature of water in an electric kettle to boiling point. Once the water is boiling steadily, she measures the change in the mass of the kettle and its contents over a period of time.
The following data are available.
Initial mass of kettle and water = 1.880 kg
Final mass of kettle and water = 1.580 kg
Time between mass measurements = 300 s
Power dissipation in the kettle = 2.5 kW
Determine the specific latent heat of vaporization of water.
(ii) Outline why your answer to (b)(i) is an overestimate of the specific latent heat of vaporization of water.
▶️Answer/Explanation
Markscheme
(i) mass lost in 300 s=(1.880-1.580)=0.3 (kg);
(energy supplied=750 kJ) (do not award credit for this line)
L=2.5 MJ kg–1; (unit must appear correctly here)
Award [2] for a bald correct answer.
(ii) energy will be transferred to surroundings; } (accept energy is lost by/from kettle to surroundings)
so calculated energy to water is too large / change in mass too large;
(hence overestimate)
Award [0] for a bald correct answer.
Treat references to energy gained by kettle as neutral; the kettle is at a constant temperature.
Question
This question is about thermal energy transfer.
A hot piece of iron is placed into a container of cold water. After a time the iron and water reach thermal equilibrium. The heat capacity of the container is negligible.
a
Define specific heat capacity.[2]
The following data are available.
Mass of water = 0.35 kg
Mass of iron = 0.58 kg
Specific heat capacity of water = 4200 J kg–1K–1
Initial temperature of water = 20°C
Final temperature of water = 44°C
Initial temperature of iron = 180°C
(i) Determine the specific heat capacity of iron.
(ii) Explain why the value calculated in (b)(i) is likely to be different from the accepted value.[5]
▶️Answer/Explanation
Markscheme
a
the energy required to change the temperature (of a substance) by 1K/°C/unit degree;
of mass 1 kg / per unit mass;
(i) use of mcΔT;
0.58×c×[180-44]=0.35×4200×[44-20];
c=447Jkg-1K-1≈450Jkg-1K-1;
(ii) energy would be given off to surroundings/environment / energy would be absorbed by container / energy would be given off through vaporization of water;
hence final temperature would be less;
hence measured value of (specific) heat capacity (of iron) would be higher;
Question
Part 2 Internal energy
Humans generate internal energy when moving, while their core temperature remains approximately constant.
a
Distinguish between the concepts of internal energy and temperature.[3]
An athlete loses 1.8 kg of water from her body through sweating during a training session that lasts one hour.
Estimate the rate of energy loss by the athlete due to sweating. The specific latent heat of evaporation of water is 2.3×106 J kg–1.[2]
▶️Answer/Explanation
Markscheme
a
internal energy:
total energy of component particles (in the human);
comprises potential energy + (random) kinetic energy;
temperature:
measure of average kinetic energy of particles;
indicates direction of (natural) flow of thermal energy;
internal energy measured in J and temperature measured
in K/°C ; (both needed)
(accept alternative suitable units)
total energy lost=2.3×106×1.8(=4.14×106J);
1.2 kW;
Part 2 Melting of the Pobeda ice island
a
The Pobeda ice island forms regularly when icebergs run aground near the Antarctic ice shelf. The “island”, which consists of a slab of pure ice, breaks apart and melts over a period of decades. The following data are available.
Typical dimensions of surface of island = 70 km × 35 km
Typical height of island = 240 m
Average temperature of the island = –35°C
Density of sea ice = 920 kg m–3
Specific latent heat of fusion of ice = 3.3×105J kg–1
Specific heat capacity of ice = 2.1×10\(^3\)J kg–1K–1
(i) Distinguish, with reference to molecular motion and energy, between solid ice and liquid water.
(ii) Show that the energy required to melt the island to form water at 0°C is about 2×1020J. Assume that the top and bottom surfaces of the island are flat and that it has vertical sides.
(iii) The Sun supplies thermal energy at an average rate of 450 W m–2 to the surface of the island. The albedo of melting ice is 0.80. Determine an estimate of the time taken to melt the island assuming that the melted water is removed immediately and that no heat is lost to the surroundings.[8]
Suggest the likely effect on the average albedo of the region in which the island was floating as a result of the melting of the Pobeda ice island.
▶️Answer/Explanation
Markscheme
a
(i) in water, molecules are able to move relative to other molecules, less movement possible in ice / in water, vibration and translation of molecules possible, in ice only vibration;
in liquid there is sufficient energy/vibration (from latent heat) to break and re-form inter-molecular bonds;
(ii) mass of ice=70000×35000×240×920(=5.4×1014kg);
energy to raise ice temperature to 0°C=5.4×1014×2.1×103×35(= 3.98×1019J);
energy to melt ice=5.4×1014×3.3×105(=1.8×1020J);
total= 2.2×1020J
(iii) energy incident=450×70000×35000(=1.1×1012Js–1m−2);
energy available for melting=1.1×1012×0.2(=2.2×1011J);
time \( = \left( {\frac{{2.2 \times {{10}^{20}}}}{{2.2 \times {{10}^{11}}}} = } \right)9.9 \times {10^8}{\rm{s}}\) or 32 years;
average albedo of ocean much smaller than (snow and) ice;
so average albedo (of Earth) is reduced;