IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.1 – Oscillations
Topic 4 Weightage : 5 %
All Questions for Topic 4.1 – Simple harmonic oscillations , Time period, frequency, amplitude, displacement and phase difference , Conditions for simple harmonic motion
Question
This question is about simple harmonic motion (SHM).
The graph shows the variation with time \(t\) of the acceleration \(a\) of an object X undergoing simple harmonic motion (SHM).
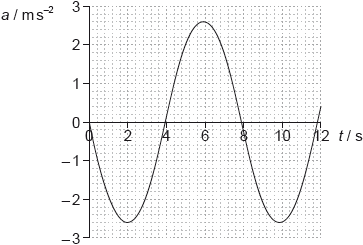
a
Define simple harmonic motion (SHM).[2]
X has a mass of 0.28 kg. Calculate the maximum force acting on X.[1]
Determine the maximum displacement of X. Give your answer to an appropriate number of significant figures.[4]
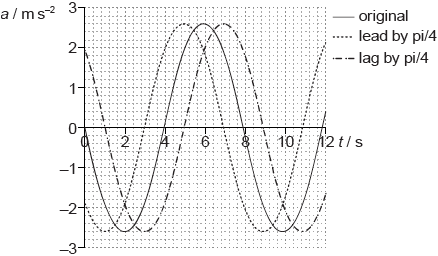
A second object Y oscillates with the same frequency as X but with a phase difference of \(\frac{\pi }{4}\). Sketch, using the graph opposite, how the acceleration of object Y varies with \(t\).[2]
▶️Answer/Explanation
Markscheme
a
force/acceleration proportional to the displacement/distance from a (fixed/equilibrium) point/mean position;
directed towards this (equilibrium) point / in opposite direction to displacement/ distance;
Allow algebra only if symbols are fully explained.
0.73 (N); (allow answer in range of 0.71 to 0.75 (N))
use of \({a_0} = – {\omega ^2}{x_0}\);
\(T = 7.9{\text{ (s)}}\) or \(\omega = 0.795\) or \(\frac{\pi }{4}{\text{ (rad}}\,{{\text{s}}^{ – 1}})\); } (allow answers in the range of T = 7.8 to 8.0 (s) or \(\omega \) = 0.785 to 0.805 (rad s–1))
\({x_0} = 4.1(1){\text{ (m)}}\); (allow answers in the range of 4.0 to 4.25 (m))
two significant figures in final answer whatever the value;
Award [4] for a bald correct answer.
shape correct, constant amplitude for new curve, minimum of 10 s shown; } (there must be some consistent lead or lag and no change in T)
lead/lag of 1 s (to within half a square by eye);
Simple harmonic motion and forced oscillations
The graph shows the variation with time of the displacement of an object undergoing simple harmonic motion.
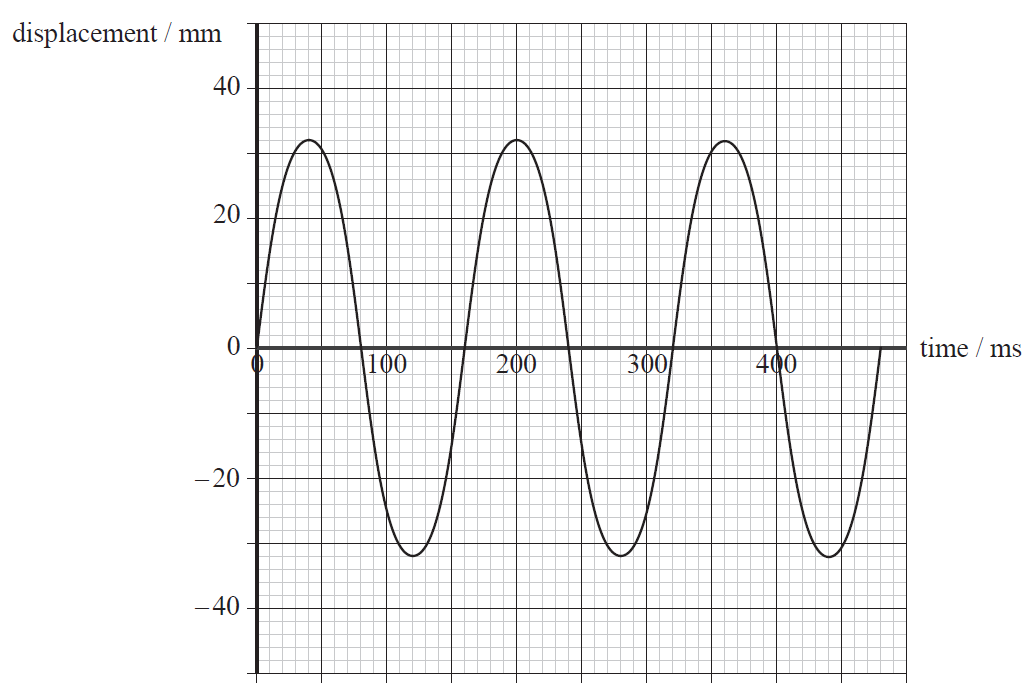
a
(i) State the amplitude of the oscillation.
(ii) Calculate the frequency of the oscillation.[3]
(i) Determine the maximum speed of the object.
(ii) Determine the acceleration of the object at 140 ms.[4]
The graph below shows how the displacement of the object varies with time. Sketch on the same axes a line indicating how the kinetic energy of the object varies with time.
You should ignore the actual values of the kinetic energy.
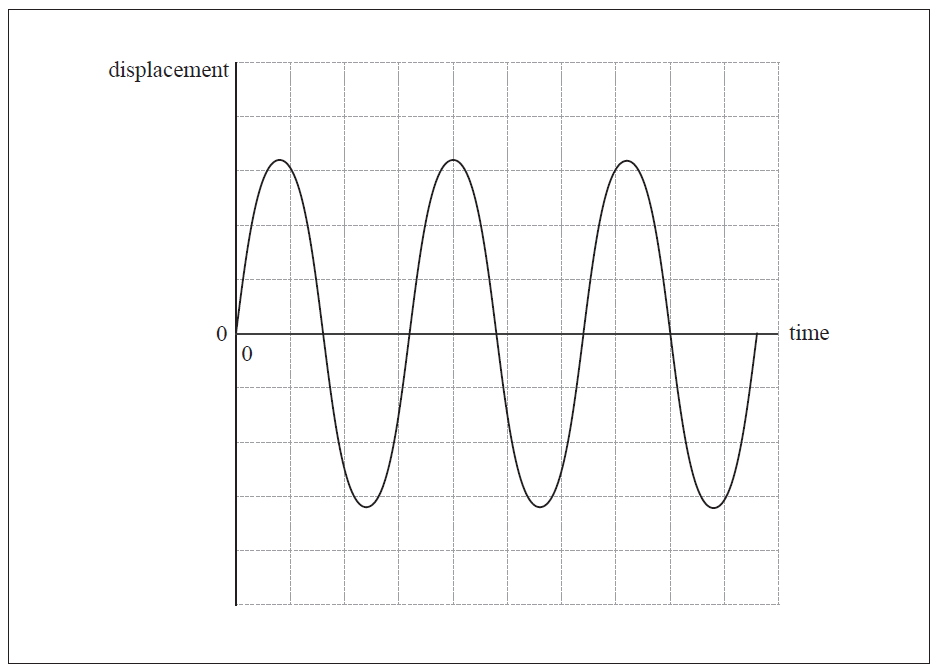 [3]
[3]
▶️Answer/Explanation
Markscheme
a
(i) 32 (mm);
(ii) period = 160 (ms);
frequency = 6.2/6.3 (Hz);
Allow ECF for incorrect period.
(i) ω=2π×6.25;
v(=39.3×32×10-3)=1.3(ms-1); (allow ECF from (a))
or
tangent drawn to graph at a point of zero displacement;
gradient calculated between 1.2 and 1.4;
(ii) displacement = 23–26 (mm);
35–40 (ms-2);
23 mm found by calculating displacement
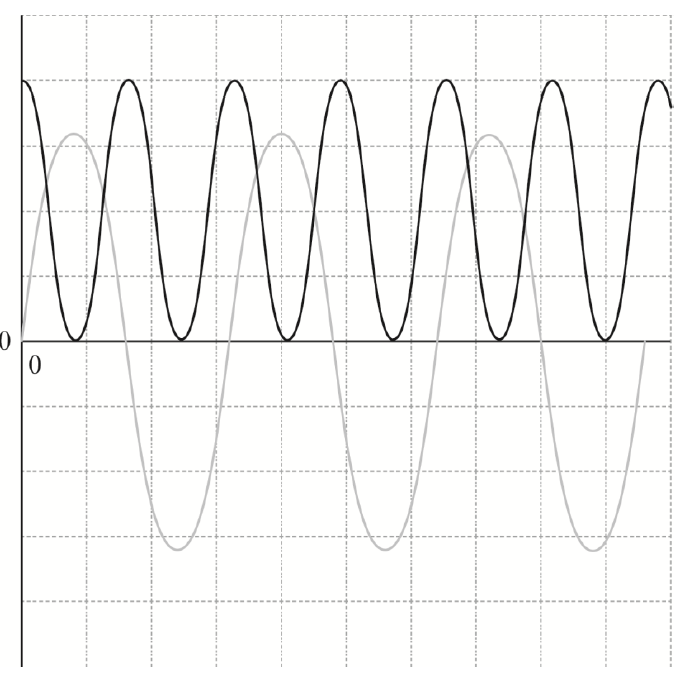
double frequency;
always positive and constant amplitude;
correct phase ie cosine squared;
Ignore amplitude value.
A minimum of one complete, original oscillation needed to award [3].
This question is in two parts. Part 1 is about simple harmonic motion (SHM) and waves. Part 2 is about wind power and the greenhouse effect.
Part 1 Simple harmonic motion (SHM) and waves
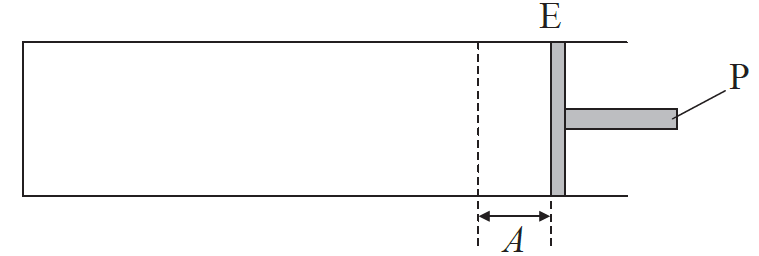
A gas is contained in a horizontal cylinder by a freely moving piston P. Initially P is at rest at the equilibrium position E.
a
The piston P is displaced a small distance A from E and released. As a result, P executes simple harmonic motion (SHM).
Define simple harmonic motion as applied to P.
The graph shows how the displacement x of the piston P in (a) from equilibrium varies with time t.
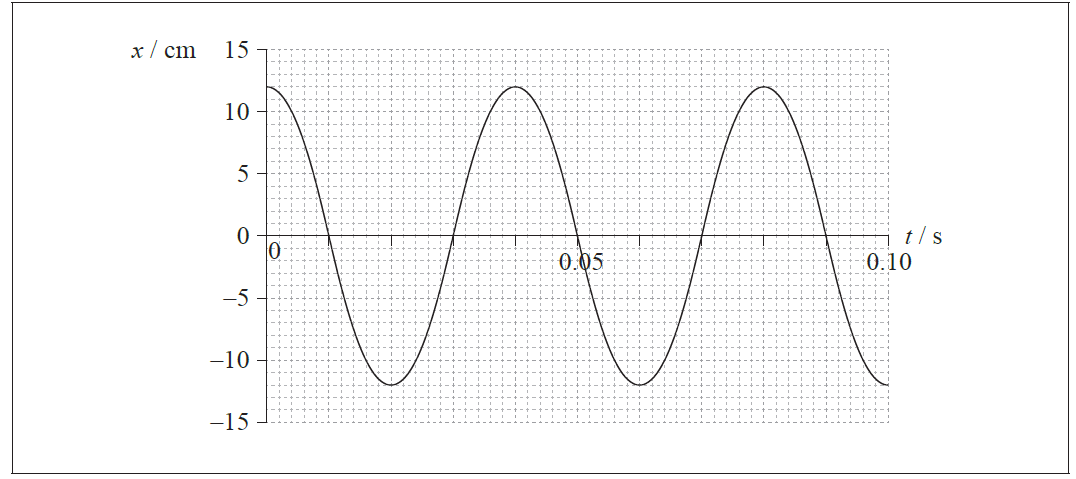
(i) State the value of the displacement A as defined in (a).
(ii) On the graph identify, using the letter M, a point where the magnitude of the acceleration of P is a maximum.
(iii) Determine, using data from the graph and your answer to (b)(i), the magnitude of the maximum acceleration of P.
(iv) The mass of P is 0.32 kg. Determine the kinetic energy of P at t=0.052 s.[7]
The oscillations of P initially set up a longitudinal wave in the gas.
(i) Describe, with reference to the transfer of energy, what is meant by a longitudinal wave.
(ii) The speed of the wave in the gas is 340 m s–1. Calculate the wavelength of the wave in the gas.[4]
▶️Answer/Explanation
Markscheme
a.
the acceleration of piston/P is proportional to its displacement from equilibrium;
and directed towards equilibrium;
There must be a clear indication what is accelerating otherwise award [1 max].
(i) 12(cm); (accept –12)
(ii) any maximum or minimum of the graph;
(iii) period= 0.04 (s); (allow clear substitution of this value)
\(\omega = \left( {\frac{{2\pi }}{T} = } \right)\frac{{2 \times 3.14}}{{0.04}} = 157\left( {{\rm{rad }}{{\rm{s}}^{ – 1}}} \right)\)
maximum acceleration=(Aω2=)0.12×1572=3.0×103(ms-2); (watch for ECF from wrong period)
(iv) at t=0.052sx=(-)4(±1)cm;
\({\rm{KE = }}\left( {\frac{1}{2}m{\omega ^2}\left[ {{A^2} – {x^2}} \right] = } \right)0.5 \times 0.32 \times {157^2}\left[ {{{0.12}^2} – {{0.04}^2}} \right] = 50\left( { \pm 7} \right)\left( {\rm{J}} \right)\);
Watch for incorrect use of cm.
Allow ECF from calculations in (b)(iii).
Do not retrospectively credit a mark for ω to (b)(iii) if it was not gained there on original marking.
Allow use of sin ωt to obtain v.
Award [2] for a bald correct answer.
(i) the direction of the oscillations/vibrations/movements of the particles (in the medium/gas);
for a longitudinal wave are parallel to the direction of the propagation of the energy of the wave;
(ii) \(f = \left( {\frac{1}{T} = } \right)\frac{1}{{0.04}} = 25\left( {{\rm{Hz}}} \right)\);
\(\lambda = \left( {\frac{v}{f} = } \right)\frac{{340}}{{25}} = 14\left( {\rm{m}} \right)\);
Award [1 max] if frequency is not clearly stated.
Allow ECF from calculations in (b)(iii).