IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.3 – Wave characteristics
Topic 4 Weightage : 10 %
All Questions for Topic 4.3 – Wavefronts and rays , Amplitude and intensity , Superposition , Polarization
a. Outline what is meant by the principle of superposition of waves.[2]
A double-slit interference pattern is observed on a screen 2.4 m from the slits.
The distance between successive maxima on the screen is 4.7 mm.
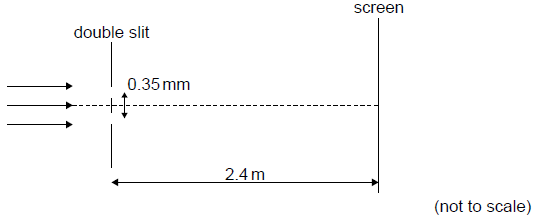
Calculate the wavelength of the light. Give your answer to an appropriate number of significant figures.[3]
Describe the appearance of the pattern on the screen.[2]
▶️Answer/Explanation
Markscheme
a.
when 2 waves meet the resultant displacement
is the «vector» sum of their individual displacements
Displacement should be mentioned at least once in MP 1 or 2.
λ = \(\frac{{4.7 \times {{10}^{ – 3}} \times 0.35 \times {{10}^{ – 3}}}}{{2.4}}\)
= 6.9 x 10–7 «m»
answer to 2 SF
Allow missed powers of 10 for MP1.
green wavelength smaller than red
fringe separation / distance between maxima decreases
Allow ECF from MP1.
bright central maximum
subsidiary maxima «on either side»
the width of the central fringe is twice / larger than the width of the subsidiary/secondary fringes/maxima
OR
intensity of pattern is decreased
Allow marks from a suitably labelled intensity graph for single slit diffraction.
Two microwave transmitters, X and Y, are placed 12 cm apart and are connected to the same source. A single receiver is placed 54 cm away and moves along a line AB that is parallel to the line joining X and Y.
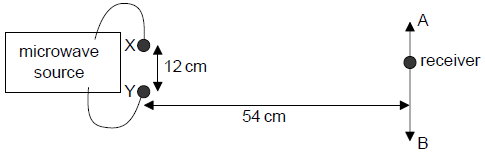
a. Maxima and minima of intensity are detected at several points along AB.
(i) Explain the formation of the intensity minima.
(ii) The distance between the central maximum and the first minimum is 7.2 cm. Calculate the wavelength of the microwaves.[4]
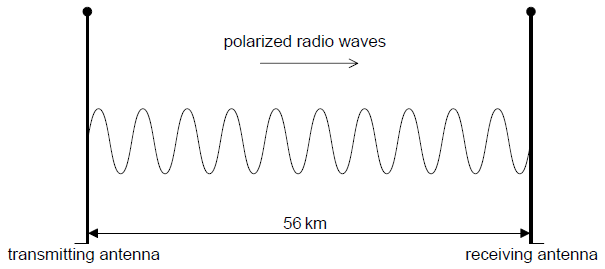
An identical antenna is used for reception. Suggest why the receiving antenna needs to be be parallel to the transmitting antenna.[2]
The receiving antenna becomes misaligned by 30° to its original position.
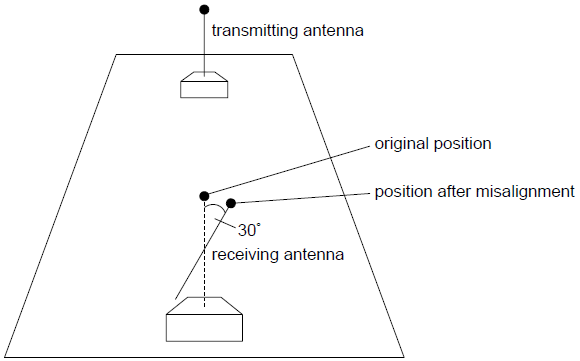
The power of the received signal in this new position is 12 μW.
(i) Calculate the power that was received in the original position.
(ii) Calculate the minimum time between the wave leaving the transmitting antenna and its reception.[3]
▶️Answer/Explanation
Markscheme
a.
i
minima = destructive interference
Allow “crest meets trough”, but not “waves cancel”.
Allow “destructive superposition” but not bald “superposition”.
at minima waves meet 180° or π out of phase
Allow similar argument in terms of effective path difference of \(\frac{\lambda }{2}\).
Allow “antiphase”, allow “completely out of phase”
Do not allow “out of phase” without angle. Do not allow \(\frac{{n\lambda }}{2}\) unless qualified to odd integers but accept \(\left( {n + \frac{1}{2}} \right)\lambda \)
ii
\(\lambda = \frac{{sd}}{D}\) or \(\lambda = \frac{{12 \times 2 \times 7.2}}{{54}} = \) or \(\lambda = \frac{{12 \times 7.2}}{{54}} = \) seen
Award [2] for a bald correct answer.
\(\lambda = \) «\(\frac{{12 \times 2 \times 7.2}}{{54}} = \)» 3.2 «cm»
Award [1 max] for 1.6 «cm»
Award [2 max] to a trigonometric solution in which candidate works out individual path lengths and equates to \(\frac{\lambda }{2}\).
ALTERNATIVE 1
the component of the polarized signal in the direction of the receiving antenna
is a maximum «when both are parallel»
ALTERNATIVE 2:
receiving antenna must be parallel to plane of polarisation
for power/intensity to be maximum
Do not accept “receiving antenna must be parallel to transmitting antenna”
ALTERNATIVE 3:
refers to Malus’ law or I = I0 cos2θ
explains that I is max when θ = 0
ALTERNATIVE 4:
an electric current is established in the receiving antenna which is proportional to the electric field
maximum current in receiving antenna requires maximum field «and so must be parallel»
i
\({I_0} = \frac{I}{{{{\cos }^2}\theta }}\) or \(\frac{{12}}{{{{\cos }^2}30}}\) seen
Award [2] for bald correct answer.
Award [1 max] for MP1 if 9 x 10-6W is the final answer (I and I0 reversed).
Award [1 max] if cos not squared (14 μW).
1.6 × 10-5«W»
Units not required but if absent assume W.
ii
1.9 × 10–4 «s»
This question is about the superposition of waves.
a.
State what is meant by the principle of superposition of waves.[1]
The diagram shows two point sources of sound, X and Y. Each source emits waves of wavelength 1.1 m and amplitude A. Over the distances shown, any decrease in amplitude can be neglected. The two sources vibrate in phase.
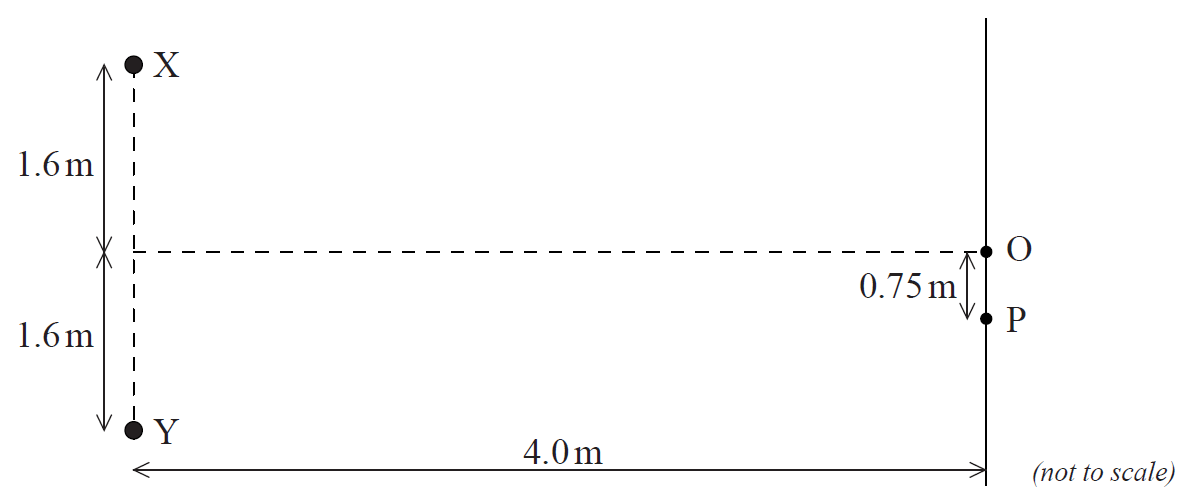
Points O and P are on a line 4.0 m from the line connecting X and Y. O is opposite the midpoint of XY and P is 0.75 m from O.
(i) Explain why the intensity of the sound at O is 4A2.
(ii) Deduce that no sound is detected at P.[5]
▶️Answer/Explanation
Markscheme
a.
(when two similar waves meet) the resultant displacement is the (vector) sum of the individual displacements;
Allow [0] for description in terms of amplitude.
(i) (constructive interference gives) amplitude 2A; intensity is proportional to square of total amplitude (=4A2);
(ii) attempted use of Pythagoras to measure path difference;
path difference =0.55 (m);
path difference = \(\frac{\lambda }{2}\) (so out of phase / destructive interference);
Attempted use of Pythagoras may appear on diagram for (b)(i).