IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.5 – Standing Waves
Topic 4 Weightage : 10 %
All Questions for Topic 4.5 – The nature of standing waves , Boundary conditions , Nodes and antinodes
Question
A pipe of length L is closed at one end. Another pipe is open at both ends and has length 2L.
What is the lowest common frequency for the standing waves in the pipes?

Answer/Explanation
Ans: B
For Pipe closed at one end
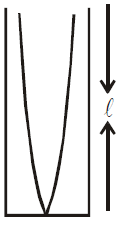
![]() (b)
(b) 
![]() (c)
(c) 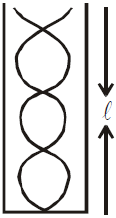
![]()
\(L=(2n+1)\frac{\;\lambda}{4} \; where \; n=0,1,2,3 \; etc..\)
\(\because v=f\lambda\)
\(\therefore f=\frac{v}{\lambda}=\frac{2n+1}{4L}\times v\)
For Pipe Open at both Ends

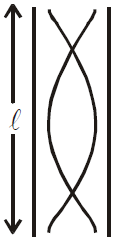
\(2L=n{}’\frac{\lambda}{2}\)
\(v= f \lambda\)
or
\(f=\frac{v}{\lambda}=\frac{n{}’}{4L} \times v\)
for common frequency
\(\frac{2n+1}{4L}\times v=\frac{n{}’}{4L} \times v\)
\(for \; 2n+1 =n{}’\; n=0 \;and\; n{}’ =1\)
\(\therefore f= \frac{v}{4L}\)
Question
A first-harmonic standing wave is formed on a vertical string of length 3.0 m using a vibration generator. The boundary conditions for this string are that it is fixed at one boundary and free at the other boundary.

The generator vibrates at a frequency of 300 Hz.
What is the speed of the wave on the string?
A. 0.90 km s–1
B. 1.2 km s–1
C. 1.8 km s–1
D. 3.6 km s–1
Answer/Explanation
Markscheme
D

\(l= (2n+1)\frac{\lambda}{4} \;\)
for first harmonic \(n=0\)
\(l=\frac{\lambda}{4}\)
Also \( v=f\lambda\)
or
\(v=300 \times 3\times 4 =3.6 \; km s^{-1}\)
Question
A pipe of fixed length is closed at one end. What is \(\frac{{{\text{third harmonic frequency of pipe}}}}{{{\text{first harmonic frequency of pipe}}}}\)?
A. \(\frac{1}{5}\)
B. \(\frac{1}{3}\)
C. 3
D. 5
Answer/Explanation
Markscheme
C
For Pipe Closed at on end
\(L=(2n+1)\frac{\;\lambda}{4} \; where \; n=0,1,2,3 \; etc..\)
\(\because v=f\lambda\)
\(\therefore f=\frac{v}{\lambda}=\frac{2n+1}{4L}\times v\)
for first harmonic \(n =0\) and third harmonic (or first overtone)\( n=1\)
\(\frac{f_{n=1}}{f_{n=0}} =\frac{\frac{3}{4L}}{\frac{1}{4L}}=3\)
Question
The frequency of the first harmonic standing wave in a pipe that is open at both ends is 200 Hz. What is the frequency of the first harmonic in a pipe of the same length that is open at one end and closed at the other?
A. 50 Hz
B. 75 Hz
C. 100 Hz
D. 400 Hz
Answer/Explanation
Markscheme
C
For Pipe Open at both Ends
\(L=n{}’\frac{\lambda}{2}\)
\(v= f \lambda\)
or
\(f=\frac{v}{\lambda}=\frac{n{}’}{2L} \times v\)
For first harmonic \(n{}’ =1 \)
\(f_{1(n=1)}=\frac{1}{2L}v =200\; Hz\) —-(1)
For Pipe closed at one end
\(L=(2n+1)\frac{\;\lambda}{4} \; where \; n=0,1,2,3 \; etc..\)
\(\because v=f\lambda\)
\(\therefore f=\frac{v}{\lambda}=\frac{2n+1}{4L}\times v\)
\(f_{2(n=0)}=\frac{1}{4L}v\) —-(2)
From eqn (1) and (2) We get
\(f_{2(n=0)} =100\; Hz\)
Question
A pipe of length L has two open ends. Another pipe of length L′ has one open end and one closed end.
The frequency of the first harmonic of both pipes is the same. What is \(\frac{{L’}}{L}\) ?
A. 2
B. \(\frac{3}{2}\)
C. 1
D. \(\frac{1}{2}\)
Answer/Explanation
Markscheme
D
For Pipe closed at one end
\(L{}’=(2n+1)\frac{\;\lambda}{4} \; where \; n=0,1,2,3 \; etc..\)
\(\because v=f\lambda\)
\(\therefore f=\frac{v}{\lambda}=\frac{2n+1}{4L{}’}\times v\)
\(f_{1(n=0)} =\frac{1}{4L{}’}\times v\)—-(1)
For Pipe Open at both Ends
\(L=n{}’\frac{\lambda}{2}\)
\(v= f \lambda\)
or
\(f=\frac{v}{\lambda}=\frac{n{}’}{2L} \times v\)
\(f_{2(n{}’=1)} =\frac{1}{2L}\times v\) —-(2)
from eqn (1) and (2) we get
\(\frac{1}{4L{}’}\times v = \frac{1}{2L}\times v\)
\(\therefore \frac{{L’}}{L} =\frac{1}{2}\)