IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 7.1 – Discrete energy and radioactivity
Topic 7 Weightage : 7%
All Questions for Topic 7.1 – Discrete energy and discrete energy levels, Transitions between energy levels, Radioactive decay, Fundamental forces and their properties, Alpha particles, beta particles and gamma rays , Half-life, Absorption characteristics of decay particles, Isotopes ,Background radiation
Question
The energy-level diagram for an atom that has four energy states is shown.
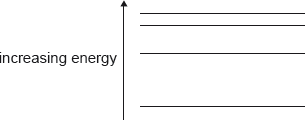
What is the number of different wavelengths in the emission spectrum of this atom?
A. 1
B. 3
C. 6
D. 7
▶️Answer/Explanation
Markscheme
C
Maximum number of spectral lines that can be emitted when an electron jumps from nth orbit is 
Here \(n\) =4
Hence number of spectral lines ( or number of different wavelength , since each spectral line is of different wavelength ) = \(\frac{4 \times 3}{2}= 6\)
Question
A simple model of an atom has three energy levels. The differences between adjacent energy levels are shown below.
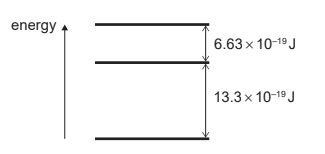
What are the two smallest frequencies in the emission spectrum of this atom?
A. 0.5 ×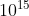 
Hz and 1.0 × 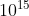Hz
B. 0.5 × 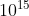Hz and 1.5 × 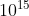Hz
C. 1.0 × 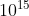Hz and 2.0 × 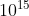Hz
D. 1.0 × 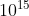Hz and 3.0 × 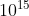Hz
▶️Answer/Explanation
Ans: C
\(6.63 \times 10^{-19}J \)and
\(13.3 \times 10^{-19}J\) are two smallest energy jump
Hence for \(6.63 \times 10^{-19}J\)
\(\nu =\frac{6.63 \times 10^{-19}}{h}\)
Now \( h = 6.6 \times 10^{-34}\)
\(\therefore\)
\(\nu =\frac{6.63 \times 10^{-19}}{h} = \frac{6.63 \times 10^{-19}}{6.6 \times 10^{-34}}= 1.0 \times 10^{15}\)
for \( 13.3 \times 10^{-19}J\)
\nu =\frac{13.3 \times 10^{-19}}{6.6 \times 10^{-34}} =2.0 \times 10^{15}\)
Hence C is answer
Question
Three of the fundamental forces between particles are
I. strong nuclear
II. weak nuclear
III. electromagnetic.
What forces are experienced by an electron?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Markscheme
C
We can also classify particles in terms of the four fundamental forces that act on them. The gravitational force acts on all particles, but its effects at the level of
subatomic particles are so weak that we need not consider that force (at least not in today’s research). The electromagnetic force acts on all electrically charged
particles; its effects are well known, and we can take them into account when we need to; we largely ignore this force in this chapter. We are left with the strong force, which is the force that binds nucleons together, and the weak force, which is involved in beta decay and similar processes.The weak force acts on all particles, the strong force only on some.
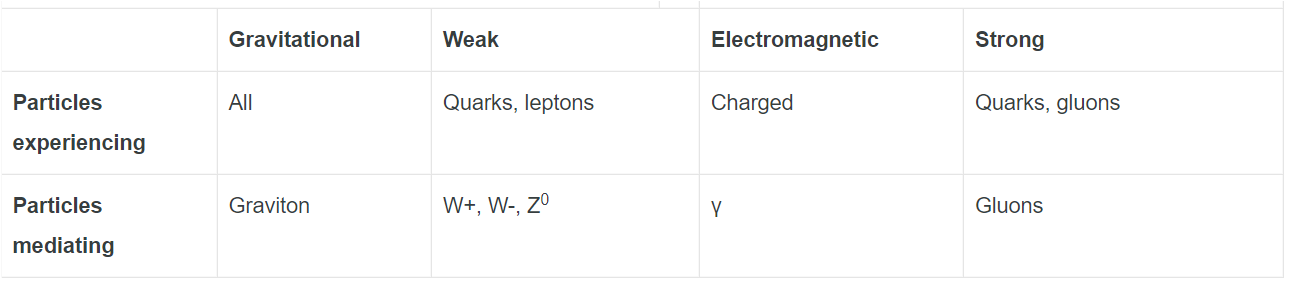
Hence Electron being charged particle it will experience Electromagnetic and Weak nuclear force.
Question
Element X decays through a series of alpha (α) and beta minus (β–) emissions. Which series of emissions results in an isotope of X?
A. 1α and 2β–
B. 1α and 4β–
C. 2α and 2β–
D. 2α and 3β–
▶️Answer/Explanation
Markscheme
A
\(_{Z}^{A}\textrm{}X\rightarrow \; x\;_{-1}^{0}\textrm{}\beta \;+y \;_{2}^{4}\textrm{}He^{+2} +\;_{Z}^{{A}’}\textrm{}Y\)
\(\alpha = He^{2+}\)
Since X and Y are isotopes hence Z should be the same.
By Conservation of charge
For one \(\alpha (He^{+2})\) there has to be \(2 \beta\)
as charge of \(He^{+2} = +2 \) and charge of \(_{-1}^{0}\textrm{}\beta = -1\)
Question
A detector, placed close to a radioactive source, detects an activity of 260 Bq. The average background activity at this location is 20 Bq. The radioactive nuclide has a half-life of 9 hours.
What activity is detected after 36 hours?
A. 15 Bq
B. 16 Bq
C. 20 Bq
D. 35 Bq
▶️Answer/Explanation
Markscheme
D
The rate of decay is given by equation
\(-\frac{dN}{dt}=\lambda N\)
The quantity \(-\frac{dN}{dt}\) gives the number of decays per unit time and is called the activity of the sample.
Thus, the activity of a radioactive sample is \(A= \lambda N\)
The activity of a radioactive substance is measured in Becquerel (Bq). One Becquerel is equal to one nuclear decay per second.
the activity at time \(t\) is derived to be
\(A_t=\frac{A_0}{2^{\frac{t}{t_{\frac{1}{2}}}}}\)
Here We have
\(A_t=\frac{A_0}{2^{\frac{t}{t_{\frac{1}{2}}}}}\)
Given that
\(A_0=260 \;Bq \; t_{\frac{1}{2}} = 9 \; hours \; t= 36 \; hours\)
since background activity is 20 Bq hence activity from radioactive source = 260-20 = 240 Bq
\(A_t =\frac{240}{2^{\frac{36}{9}}}=\frac{240}{2^4} \approx 15\)
Hence Total Activities detected = Activity due to radioactive source + Average Background Activity = 20 + 15 = 35 Bq
Question
The energy-level diagram for an atom that has four energy states is shown.
What is the number of different wavelengths in the emission spectrum of this atom?
A. 1
B. 3
C. 6
D. 7
▶️Answer/Explanation
Markscheme
C
Maximum number of spectral lines that can be emitted when an electron jumps from nth orbit is
Here \(n\) =4
Hence number of spectral lines ( or number of different wavelength , since each spectral line is of different wavelength ) = \(\frac{4 \times 3}{2}= 6\)
Related Links