IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 7.2 Nuclear reactions
Topic 7 Weightage : 3 %
All Questions for Topic 7.2 – The unified atomic mass unit , Mass defect and nuclear binding energy , Nuclear fission and nuclear fusion
Question
(a) One possible fission reaction of uranium-235 (U-235) is
The following data are available.
Mass of one atom of U-235 = 235 u
Binding energy per nucleon for U-235 = 7.59 MeV
Binding energy per nucleon for Xe-140 = 8.29 MeV
Binding energy per nucleon for Sr-94 = 8.59 MeV
(i) State what is meant by binding energy of a nucleus. [1]
(ii) Outline why quantities such as atomic mass and nuclear binding energy are often expressed in non-SI units. [1]
(iii) Show that the energy released in the reaction is about 180 MeV. [1]
(b) A nuclear power station uses U-235 as fuel. Assume that every fission reaction of U-235 gives rise to 180 MeV of energy.
(i) Estimate, in J kg–1, the specific energy of U-235. [2]
(ii) The power station has a useful power output of 1.2 GW and an efficiency of 36 %.
Determine the mass of U-235 that undergoes fission in one day. [2]
(iii) The specific energy of fossil fuel is typically 30 MJ kg–1. Suggest, with reference to your answer to (b)(i), one advantage of U-235 compared with fossil fuels in a power station. [1]
▶️Answer/Explanation
Ans:
a i
energy required to «completely» separate the nucleons
OR
energy released when a nucleus is formed from its constituent nucleons ✓
a ii the values «in SI units» would be very small
a iii 140 × 8.29 + 94 × 8.59 – 235 × 7.59 OR 184 «MeV»
b i see = « «energy=» 180 ×106 × 1.60 ×10-19 AND « mass=» 235 × 1.66 × 10-27 , 7.4 × 1013 «J kg-1 »
b ii
energy produced in one day = \(\frac{1.2\times 109\times 22\times 3600}{0.36}\) = 2.9 ×1014 «J »
mass =\(\frac{2.9\times 10^{14}}{7.4\times 10^{15}}\)
b iii
«specific energy of uranium is much greater than that of coal, hence» more energy can be
produced from the same mass of fuel / per kg
OR
less fuel can be used to create the same amount of energy ✓
This question is about binding energy and mass defect.
(i) The nuclear mass of the nuclide helium-3 \(\left( {_2^3{\text{He}}} \right)\) is 3.014931 u. Show that the binding energy per nucleon for the nuclide is about 2.6 MeV.
(ii) The binding energy per nucleon for deuterium \(\left( {_1^2{\text{H}}} \right)\) is 1.11 MeV. Calculate the energy change in the following reaction.
\[_1^2{\text{H}} + _1^1{\text{H}} \to _2^3{\text{HE}} + \gamma \]
(iii) The cross on the grid shows the binding energy per nucleon and nucleon number A of the nuclide nickel-62.
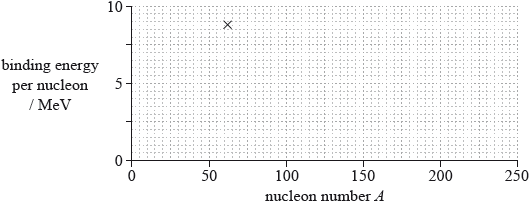
On the grid, sketch a graph to show how the average binding energy per nucleon varies with nucleon number A.
(iv) State and explain, with reference to your sketch graph, whether energy is released or absorbed in the reaction in (b)(ii).
▶️Answer/Explanation
Markscheme
(i) mass defect \(\left( {[2 \times 1.007276 + 1.008665] – 3.014931 = } \right){\text{ }}0.008286{\text{ u}}\);
binding energy per nucleon \(\left( {\frac{{0.008286 \times 931.5}}{3} = } \right)\frac{{7.7}}{3}\)\(\,\,\,\)or\(\,\,\,\)\(2.58{\text{ (MeV)}}\);
(ii) binding energy of left-hand side \( = 1.11 \times 2\) and binding energy of right-hand side \( = 3 \times 2.6\); } (both needed) (allow ECF)
energy release \( = 5.58{\text{ (MeV)}}\); (ignore sign)
(iii) line goes through Ni point and nickel is the maximum ±2 small squares horizontally; } (allow Fe-56 as maximum – this is just outside the range allowed)
line starts at 0, downward trend for A after 62, trend after nickel less steep than before;
Line must go through part of the X to award first marking point.
Line must not flatten out to award second marking point.
Allow smooth curve for low A.
Allow incorrect variations at low A.
(iv) nucleus produced in the reaction is higher up the curve than the reactants / OWTTE; } (must see reference to graph)
reference to binding energy/other valid reason results in energy release;
Award [0] for a bald correct answer.
Award [0] for any discussion of fission.