IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 7.3 The structure of matter
Topic 7 Weightage : 3 %
All Questions for Topic 7.3 – Quarks, leptons and their antiparticles , Hadrons, baryons and mesons , The conservation laws of charge, baryon number, lepton number and strangeness , The nature and range of the strong nuclear force, weak nuclear force and electromagnetic force , Exchange particles , Feynman diagrams , Confinement , The Higgs boson
In beta minus (β−) decay a d quark decays into a u quark, an electron and an electron antineutrino.
a.
Show that lepton number is conserved in this decay.[1]
A nucleus of phosphorus-32 \(\left( {{}_{15}^{32}{\rm{P}}} \right)\) decays by beta minus (β−) decay into a nucleus of sulfur-32 \(\left( {{}_{16}^{32}{\rm{S}}} \right)\). The binding energy per nucleon of \({}_{15}^{32}{\rm{P }}\) is 8.398 MeV and for \({}_{16}^{32}{\rm{S }}\) it is 8.450 MeV.
(i) State what is meant by the binding energy of a nucleus.
(ii) Determine the energy released in this decay.[3]
Quarks were hypothesized long before their existence was experimentally verified. Discuss the reasons why physicists developed a theory that involved quarks.[3]
Answer/Explanation
Markscheme
a.
«lepton number on» LHS = 0 and «lepton number on» RHS = 0 +1−1
OR
quarks have no/0/zero lepton number and the lepton number for electron and the antineutrino cancel
(i)
energy released when a nucleus forms from constituent nucleons
OR
minimum energy needed/work done to break a nucleus up into its constituent nucleons
Do not allow reference to “atom”.
Award [0] for “energy to assemble nucleus”.
Do not allow “particles”, “constituents” or “components” for “nucleons”.
(ii)
«energy/mass difference =» 8.450 – 8.398 «= 0.052 MeV»
Q = 1.7 or 1.66 or 1.664 MeV
OR
2.66 × 10–13 J
quark theory is simpler OR Occam’s razor example OR simple model explains complex observations
quotes experiment that led to quark theory, eg deep inelastic scattering or electron scattering
model incorporates strong/weak interactions/forces between protons and neutrons
model incorporates conservation rules
model explains differences between neutrons and protons OR explains decay of neutron to proton
a.
A particular K meson has a quark structure \({\rm{\bar u}}\)s. State the charge, strangeness and baryon number for this meson.
 [2]
[2]
The Feynman diagram shows the changes that occur during beta minus (β–) decay.
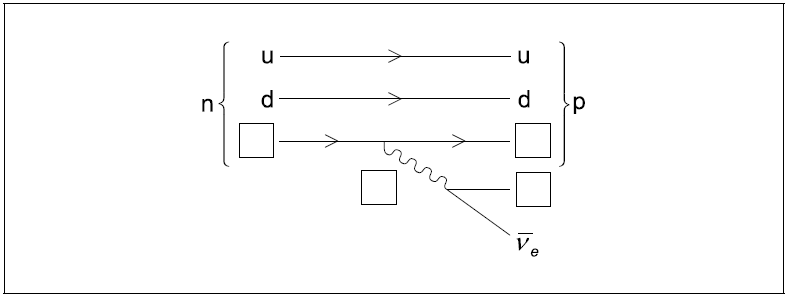
Label the diagram by inserting the four missing particle symbols and the direction of the arrows for the decay particles.[3]
C-14 decay is used to estimate the age of an old dead tree. The activity of C-14 in the dead tree is determined to have fallen to 21% of its original value. C-14 has a half-life of 5700 years.
(i) Explain why the activity of C-14 in the dead tree decreases with time.
(ii) Calculate, in years, the age of the dead tree. Give your answer to an appropriate number of significant figures.[4]
Answer/Explanation
Markscheme
a.
charge: –1«e» or negative or K−
strangeness: –1
baryon number: 0
Negative signs required.
Award [2] for three correct answers, [1 max] for two correct answer and [0] for one correct answer.
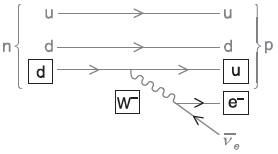
correct symbols for both missing quarks
exchange particle and electron labelled W or W– and e or e–
Do not allow W+ or e+ or β+. Allow β or β–.
arrows for both electron and anti-neutrino correct
Allow ECF from previous marking point.
i
number of C-14 atoms/nuclei are decreasing
OR
decreasing activity proportional to number of C-14 atoms/nuclei
OR
A = A0e–λt so A decreases as t increases
Do not allow “particles”
Must see reference to atoms or nuclei or an equation, just “C-14 is decreasing” is not enough.
ii
0.21 = (0.5)n
OR
\(0.21 = {e^{ – \left( {\frac{{\ln 2 \times t}}{{5700}}} \right)}}\)
n = 2.252 half-lives or t =1 2834 «y»
Early rounding to 2.25 gives 12825 y
13000 y rounded correctly to two significant figures:
Both needed; answer must be in year for MP3.
Allow ECF from MP2.
Award [3] for a bald correct answer.
This question is about the Rutherford model of the atom.
The isotope gold-197 \(\left( {_{\;{\text{79}}}^{{\text{197}}}{\text{Au}}} \right)\) is stable but the isotope gold-199 \(_{\;{\text{79}}}^{{\text{199}}}{\text{Au}}\) is not.
A nucleus of \(_{\;{\text{79}}}^{{\text{199}}}{\text{Au}}\) decays to a nucleus of \(_{\;{\text{80}}}^{{\text{199}}}{\text{Hg}}\). State the two particles, other than \(\gamma \)-photon, emitted in this decay.
Answer/Explanation
Markscheme
electron/beta (condone lack of sign);
anti neutrino / \(\bar v\);
Allow undefined symbols if unambiguous