IB DP Physics 7.3 – The structure of matter Question Bank SL Paper 3

IB DP PhysicsIB DP Maths IB DP ChemistryIB DP Biology

Question

This question is about quarks.

An interaction between an electron and a positron can lead to the production of hadrons via the reaction
\[{e^ – } + {e^ + } \to u + \bar u\]
where u is an up quark. This process involves the electromagnetic interaction.

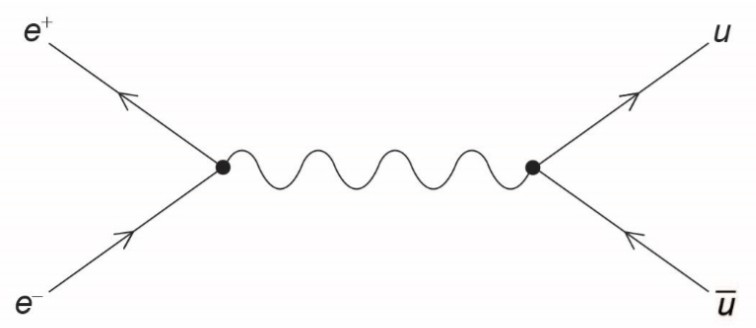
a.Draw a Feynman diagram for this interaction.[2]

b.Outline, with reference to the strong interaction, why hadrons are produced in the reaction.[2]

▶️Answer/Explanation

Markscheme

particles correctly labelled and interaction correctly shown;
arrow directions correct;

strong (colour) interaction increases with separation requiring high energy;
high energy allows creation of hadrons/quarks;
confinement requires the formation of two quarks, not one;

Question

This question is about fundamental interactions.

The Feynman diagram shows the decay of a K⁺ meson into three other particles.

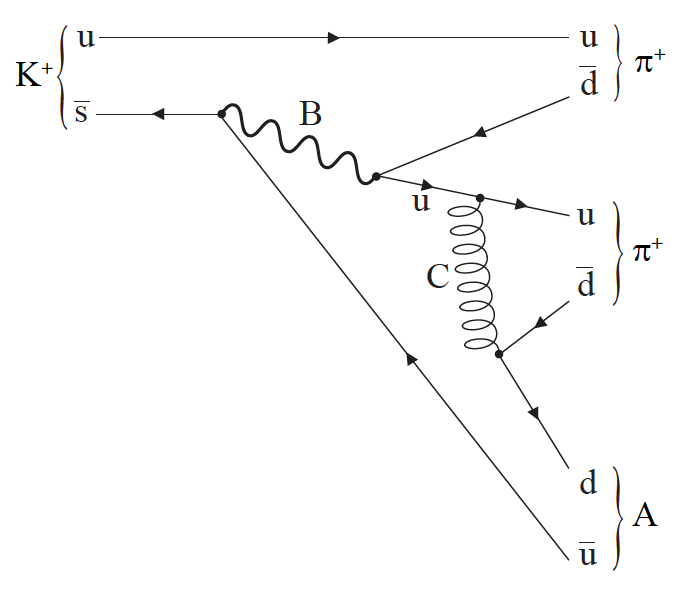
a.Identify particle A.[1]

b.(i) Identify the interaction whose exchange particle is represented by B.

(ii) Identify the exchange particle labelled C.[2]

c.Outline how the concept of strangeness applies to the decay of a K⁺ meson shown in this Feynman diagram.[2]

▶️Answer/Explanation

Markscheme

\(\pi \)^–/ antiparticle of \(\pi \)⁺

Do not award mark if sign is omitted.

(i) (electro) weak;

(ii) gluon/photon;

strangeness is not conserved (in interaction B therefore it is a weak interaction);
strangeness is conserved in interaction C/in strong and electromagnetic interactions;