IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 8.1 – Energy sources
Topic 8 Weightage : 7 %
All Questions for Topic 8.1 – Specific energy and energy density of fuel sources , Sankey diagrams , Primary energy sources , Electricity as a secondary and versatile form of energy , Renewable and non-renewable energy sources
Two renewable energy sources are solar and wind.
An alternative generation method is the use of wind turbines.
The following data are available:
Length of turbine blade = 17 m
Density of air = 1.3 kg m–3
Average wind speed = 7.5 m s–1
a.
Describe the difference between photovoltaic cells and solar heating panels.[1]
A solar farm is made up of photovoltaic cells of area 25 000 m2. The average solar intensity falling on the farm is 240 W m–2 and the average power output of the farm is 1.6 MW. Calculate the efficiency of the photovoltaic cells.[2]
Determine the minimum number of turbines needed to generate the same power as the solar farm.[3]
Explain two reasons why the number of turbines required is likely to be greater than your answer to (c)(i).[2]
▶️Answer/Explanation
Markscheme
a.
solar heating panel converts solar/radiation/photon/light energy into thermal energy AND photovoltaic cell converts solar/radiation/photon/light energy into electrical energy
Accept internal energy of water.
power received = 240 × 25000 = «6.0 MW»
efficiency «\( = \frac{{1.6}}{{6.0}}\) = 0.27 / 27%
area = \(\pi \) × 172 «= 908m2»
power = \(\frac{1}{2} \times 908 \times 1.3 \times {7.5^3}\) «= 0.249 MW»
number of turbines «\( = \frac{{1.6}}{{0.249}} = 6.4\)» = 7
Only allow integer value for MP3.
Award [2 max] for 25 turbines (ECF from incorrect power)
Award [2 max] for 26 turbines (ECF from incorrect radius)
«efficiency is less than 100% as»
not all KE of air can be converted to KE of blades
OR
air needs to retain KE to escape
thermal energy is lost due to friction in turbine/dynamo/generator
Allow velocity of air after turbine is not zero.
In a pumped storage hydroelectric system, water is stored in a dam of depth 34 m.
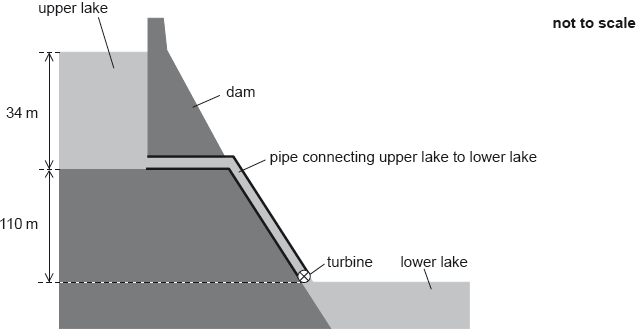
The water leaving the upper lake descends a vertical distance of 110 m and turns the turbine of a generator before exiting into the lower lake.
Water flows out of the upper lake at a rate of 1.2 × 105 m3 per minute. The density of water is 1.0 × 103 kg m–3.
a.i.
Estimate the specific energy of water in this storage system, giving an appropriate unit for your answer.[2]
Show that the average rate at which the gravitational potential energy of the water decreases is 2.5 GW.[3]
The storage system produces 1.8 GW of electrical power. Determine the overall efficiency of the storage system.[1]
After the upper lake is emptied it must be refilled with water from the lower lake and this requires energy. Suggest how the operators of this storage system can still make a profit.[1]
▶️Answer/Explanation
Markscheme
a.i.
Average height = 127 «m»
Specific energy «= \(\frac{{mg\bar h}}{m} = g\bar h\) = 9.81 × 127» = 1.2 × 103 J kg–1
Unit is essential
Allow g = 10 gives 1.3 × 103 J kg–1
Allow ECF from 110 m
(1.1 × 103 J kg–1) or 144 m
(1.4 × 103 J kg–1)[2 marks]
mass per second leaving dam is \(\frac{{1.2 \times {{10}^5}}}{{60}}\) × 103 = «2.0 × 106 kg s–1»
rate of decrease of GPE is = 2.0 × 106 × 9.81 × 127
= 2.49 × 109 «W» /2.49 «GW»
Do not award ECF for the use of 110 m or 144 m
Allow 2.4 GW if rounded value used from (a)(i) or 2.6 GW if g = 10 is used[3 marks]
efficiency is «\(\frac{{1.8}}{{2.5}}\) =» 0.72 / 72%[1 mark]
water is pumped back up at times when the demand for/price of electricity is low[1 mark]
a.
Outline, with reference to energy changes, the operation of a pumped storage hydroelectric system.[2]
The hydroelectric system has four 250 MW generators. The specific energy available from the water is 2.7 kJ kg–1. Determine the maximum time for which the hydroelectric system can maintain full output when a mass of 1.5 x 1010 kg of water passes through the turbines.[2]
Not all the stored energy can be retrieved because of energy losses in the system. Explain one such loss.[1]
At the location of the hydroelectric system, an average intensity of 180 W m–2 arrives at the Earth’s surface from the Sun. Solar photovoltaic (PV) cells convert this solar energy with an efficiency of 22 %. The solar cells are to be arranged in a square array. Determine the length of one side of the array that would be required to replace the
hydroelectric system.[2]
▶️Answer/Explanation
Markscheme
a.
PE of water is converted to KE of moving water/turbine to electrical energy «in generator/turbine/dynamo»
idea of pumped storage, ie: pump water back during night/when energy cheap to buy/when energy not in demand/when there is a surplus of energy
total energy = «2.7 x 103 x 1.5 x 1010 =» 4.05 x 1013 «J»
time = «\(\frac{{4.0 \times {{10}^{13}}}}{{4 \times 2.5 \times {{10}^8}}}\)» 11.1h or 4.0 x 104 s
For MP2 the unit must be present.
friction/resistive losses in walls of pipe/air resistance/turbulence/turbine and generator bearings
thermal energy losses, in electrical resistance of components
water requires kinetic energy to leave system so not all can be transferred
Must see “seat of friction” to award the mark.
Do not allow “friction” bald.
area required \( = \frac{{1 \times {{10}^9}}}{{0.22 \times 180}}\) «= 2.5 x 107 m2»
length of one side \( = \sqrt {area} = 5.0\) k«m»
Two renewable energy sources are solar and wind.
An alternative generation method is the use of wind turbines.
The following data are available:
Length of turbine blade = 17 m
Density of air = 1.3 kg m–3
Average wind speed = 7.5 m s–1
a.
Describe the difference between photovoltaic cells and solar heating panels.[1]
A solar farm is made up of photovoltaic cells of area 25 000 m2. The average solar intensity falling on the farm is 240 W m–2 and the average power output of the farm is 1.6 MW. Calculate the efficiency of the photovoltaic cells.[2]
Determine the minimum number of turbines needed to generate the same power as the solar farm.[3]
Explain two reasons why the number of turbines required is likely to be greater than your answer to (c)(i).[2]
▶️Answer/Explanation
Markscheme
a.
solar heating panel converts solar/radiation/photon/light energy into thermal energy AND photovoltaic cell converts solar/radiation/photon/light energy into electrical energy
Accept internal energy of water.
power received = 240 × 25000 = «6.0 MW»
efficiency «\( = \frac{{1.6}}{{6.0}}\) = 0.27 / 27%
area = \(\pi \) × 172 «= 908m2»
power = \(\frac{1}{2} \times 908 \times 1.3 \times {7.5^3}\) «= 0.249 MW»
number of turbines «\( = \frac{{1.6}}{{0.249}} = 6.4\)» = 7
Only allow integer value for MP3.
Award [2 max] for 25 turbines (ECF from incorrect power)
Award [2 max] for 26 turbines (ECF from incorrect radius)
«efficiency is less than 100% as»
not all KE of air can be converted to KE of blades
OR
air needs to retain KE to escape
thermal energy is lost due to friction in turbine/dynamo/generator
Allow velocity of air after turbine is not zero.