IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 8.2 Thermal energy transfer
Topic 8 Weightage : 3 %
All Questions for Topic 8.2 – Conduction, convection and thermal radiation , Black-body radiation , Albedo and emissivity , The solar constant , The greenhouse effect , Energy balance in the Earth surface–atmosphere system
This question is in two parts. Part 1 is about solar radiation and the greenhouse effect. Part 2 is about orbital motion.
Part 1 Solar radiation and the greenhouse effect
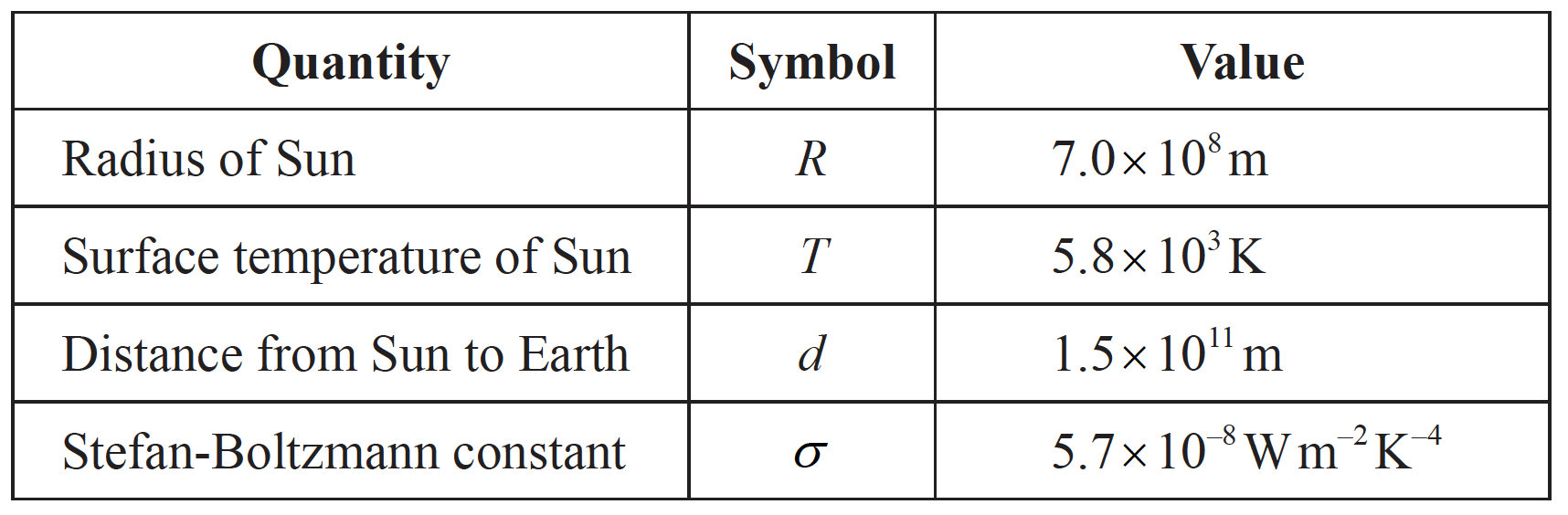
The following data are available.
Part 2 Orbital motion
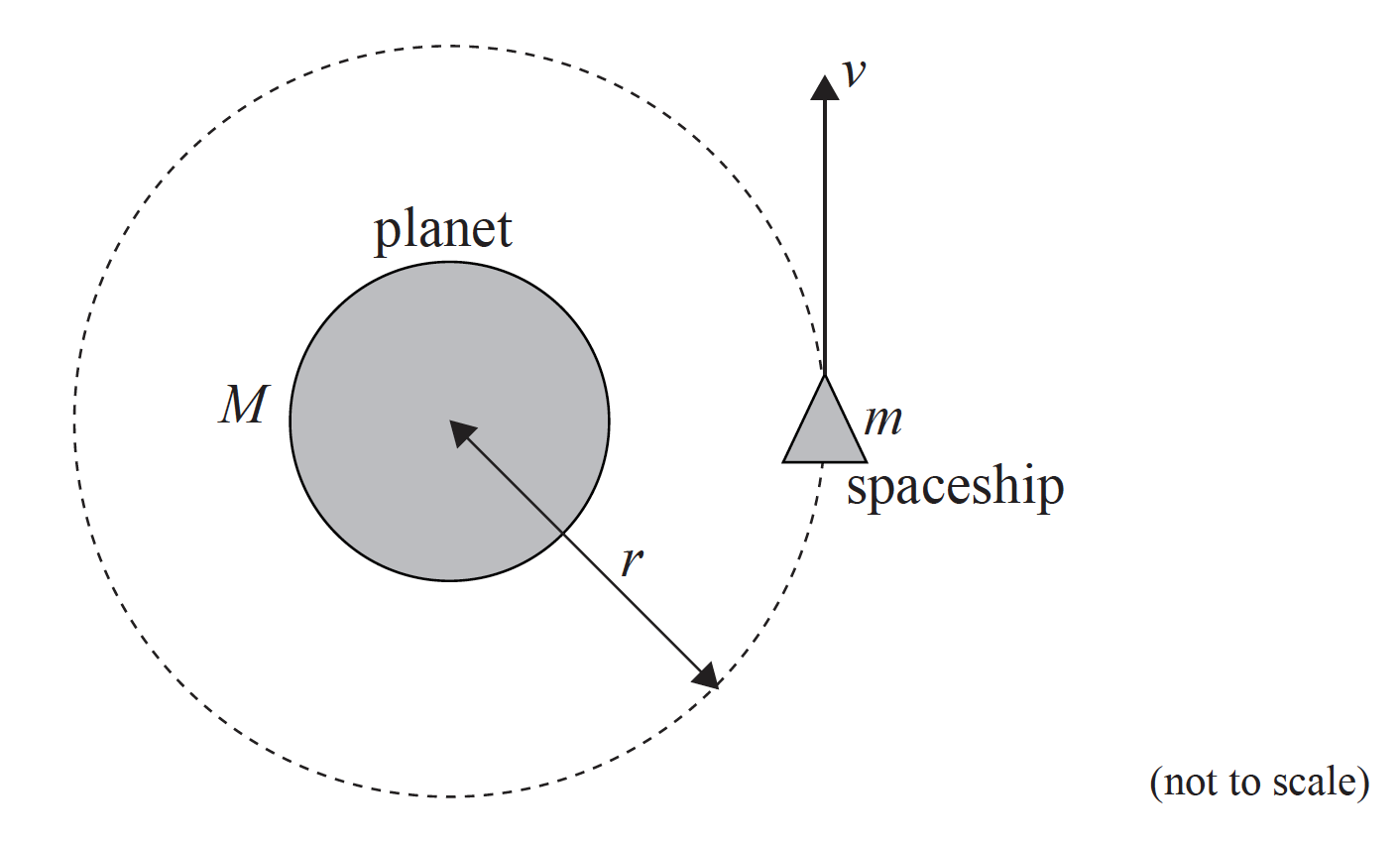
A spaceship of mass m is moving at speed v in a circular orbit of radius r around a planet of mass M.
a.
State the Stefan-Boltzmann law for a black body.[2]
Deduce that the solar power incident per unit area at distance d from the Sun is given by
\(\frac{{\sigma {R^2}{T^4}}}{{{d^2}}}\).[2]
Calculate, using the data given, the solar power incident per unit area at distance d from the Sun.[2]
State two reasons why the solar power incident per unit area at a point on the surface of the Earth is likely to be different from your answer in (c).[2]
The average power absorbed per unit area at the Earth’s surface is 240Wm–2. By treating the Earth’s surface as a black body, show that the average surface temperature of the Earth is approximately 250K.[2]
Explain why the actual surface temperature of the Earth is greater than the value in (e).[3]
(i) Identify the force that causes the centripetal acceleration of the spaceship.
(ii) Explain why astronauts inside the spaceship would feel “weightless”, even though there is a force acting on them.[4]
Deduce that the speed of the spaceship is \(v = \sqrt {\frac{{GM}}{r}} \).[2]
The table gives equations for the forms of energy of the orbiting spaceship.
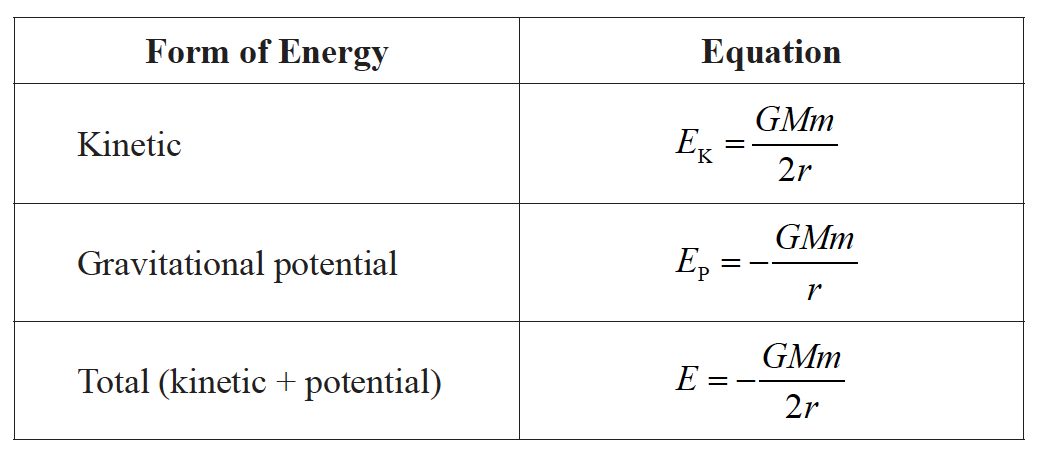
The spaceship passes through a cloud of gas, so that a small frictional force acts on the spaceship.
(i) State and explain the effect that this force has on the total energy of the spaceship.
(ii) Outline the effect that this force has on the speed of the spaceship.[4]
▶️Answer/Explanation
Markscheme
a.
power/energy per second emitted is proportional to surface area;
and proportional to fourth power of absolute temperature / temperature in K;
Accept equation with symbols defined.
solar power given by \(4\pi {R^2}\sigma {T^4}\);
spreads out over sphere of surface area \(4\pi {d^2}\);
Hence equation given.
\(\left( {\frac{{\sigma {R^2}{T^4}}}{{{d^2}}} = } \right)\frac{{5.7 \times {{10}^{ – 8}} \times {{\left[ {7.0 \times {{10}^8}} \right]}^2} \times {{\left[ {5.8 \times {{10}^3}} \right]}^4}}}{{{{\left[ {1.5 \times {{10}^{11}}} \right]}^2}}}\);
=1.4×103(Wm-2);
Award [2] for a bald correct answer.
some energy reflected;
some energy absorbed/scattered by atmosphere;
depends on latitude;
depends on time of day;
depends on time of year;
depends on weather (eg cloud cover) at location;
power output of Sun varies;
Earth-Sun distance varies;
power radiated=power absorbed;
\(T = {}^4\sqrt {\frac{{240}}{{5.7 \times {{10}^{ – 8}}}}} \left( { = 250{\rm{K}}} \right)\);
Accept answers given as 260 (K).
radiation from Sun is re-emitted from Earth at longer wavelengths;
greenhouse gases in the atmosphere absorb some of this energy;
and radiate some of it back to the surface of the Earth;
(i) gravitational force / gravitational attraction / weight; (do not accept gravity)
(ii) astronauts and spaceship have the same acceleration;
acceleration is towards (centre of) planet;
so no reaction force between astronauts and spaceship;
or
astronauts and spaceships are both falling towards the (centre of the) planet;
at the same rate;
so no reaction force between astronauts and spaceship;
gravitational force equated with centripetal force / \(\frac{{GmM}}{{{r^2}}} = \frac{{m{v^2}}}{r}\);
\( \Rightarrow {v^2} = \frac{{GM}}{r} \Rightarrow \left( {v = \sqrt {\frac{{GM}}{r}} } \right)\);
(i) thermal energy is lost;
total energy decreases;
(ii) since E decreases, r also decreases;
as r decreases v increases / Ek increases so v increases;
The Sun has a radius of 7.0×108m and is a distance 1.5×1011 m from Earth. The surface temperature of the Sun is 5800 K.
The average surface temperature of the Earth is actually 288 K.
Suggest how the greenhouse effect helps explain the difference between the temperature estimated in (c) and the actual temperature of the Earth.
▶️Answer/Explanation
Markscheme
the emitted radiation is in the infrared/IR/long wavelength/low frequency region
«greenhouse» gases in the atmosphere absorb «infrared» radiation
radiated in all directions «including back down to Earth» warming the Earth
Do not allow “traps the heat”.
Must see clear implication somewhere in response that gases are in the atmosphere for MP2.
Must see sense that Earth temperature is raised for MP3.